山东省淄博市2019年中考数学试卷(A卷)
试卷更新日期:2019-07-09 类型:中考模拟
一、单选题
-
1. 比﹣2小1的数是( )A、﹣3 B、﹣1 C、1 D、32. 国产科幻电影《流浪地球》上映17日,票房收入突破40亿元人民币,将40亿用科学记数法表示为( )A、 B、 C、 D、3. 下列几何体中,其主视图、左视图和俯视图完全相同的是( )A、
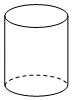 B、
B、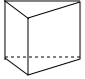 C、
C、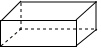 D、
D、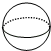 4. 如图,小明从 处沿北偏东 方向行走至点 处,又从点 处沿东偏南 方向行走至点 处,则 等于( )
4. 如图,小明从 处沿北偏东 方向行走至点 处,又从点 处沿东偏南 方向行走至点 处,则 等于( )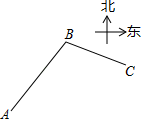 A、 B、 C、 D、5. 解分式方程 时,去分母变形正确的是( )A、 B、 C、 D、6. 与下面科学计算器的按键顺序:
A、 B、 C、 D、5. 解分式方程 时,去分母变形正确的是( )A、 B、 C、 D、6. 与下面科学计算器的按键顺序:
对应的计算任务是( )
A、 B、 C、 D、7. 如图,矩形内有两个相邻的正方形,其面积分别为2和8,则图中阴影部分的面积为( )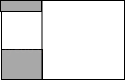 A、 B、2 C、 D、68. 如图,在 中, , , 为 边上的一点,且 .若 的面积为 ,则 的面积为( )
A、 B、2 C、 D、68. 如图,在 中, , , 为 边上的一点,且 .若 的面积为 ,则 的面积为( )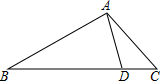 A、 B、 C、 D、9. 若 , ,则以 , 为根的一元二次方程是( )A、 B、 C、 D、
A、 B、 C、 D、9. 若 , ,则以 , 为根的一元二次方程是( )A、 B、 C、 D、二、填空题
-
10. 单项式 的次数是 .11. 分解因式: =.12. 如图,在正方形网格中,格点 绕某点顺时针旋转角 得到格点 ,点 与点 ,点 与点 ,点 与点 是对应点,则 度.
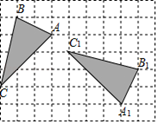 13. 某校欲从初三级部3名女生,2名男生中任选两名学生代表学校参加全市举办的“中国梦•青春梦”演讲比赛,则恰好选中一男一女的概率是 .14. 如图,在以 为直角顶点的等腰直角三角形纸片 中,将 角折起,使点 落在 边上的点 (不与点 , 重合)处,折痕是 .
13. 某校欲从初三级部3名女生,2名男生中任选两名学生代表学校参加全市举办的“中国梦•青春梦”演讲比赛,则恰好选中一男一女的概率是 .14. 如图,在以 为直角顶点的等腰直角三角形纸片 中,将 角折起,使点 落在 边上的点 (不与点 , 重合)处,折痕是 .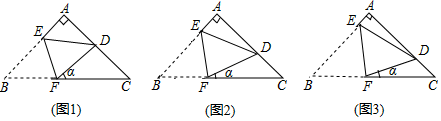
如图,当 时, ;
如图,当 时, ;
如图,当 时, ;
……
依此类推,当 ( 为正整数)时, .
三、解答题
-
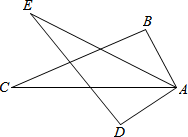
15. 解不等式 .16. 已知,在如图所示的“风筝”图案中, , , .求证: .
 17. 文明交流互鉴是推动人类文明进步和世界和平发展的重要动力.2019年5月“亚洲文明对话大会”在北京成功举办,引起了世界人民的极大关注.某市一研究机构为了了解10~60岁年龄段市民对本次大会的关注程度,随机选取了100名年龄在该范围内的市民进行了调查,并将收集到的数据制成了尚不完整的频数分布表、频数分布直方图和扇形统计图,如下所示:
17. 文明交流互鉴是推动人类文明进步和世界和平发展的重要动力.2019年5月“亚洲文明对话大会”在北京成功举办,引起了世界人民的极大关注.某市一研究机构为了了解10~60岁年龄段市民对本次大会的关注程度,随机选取了100名年龄在该范围内的市民进行了调查,并将收集到的数据制成了尚不完整的频数分布表、频数分布直方图和扇形统计图,如下所示:组别
年龄段
频数(人数)
第1组
5
第2组
第3组
35
第4组
20
第5组
15
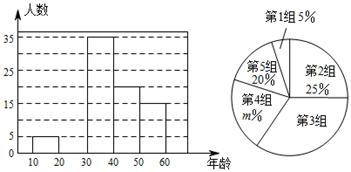 (1)、请直接写出 , , 第3组人数在扇形统计图中所对应的圆心角是度.(2)、请补全上面的频数分布直方图;(3)、假设该市现有10~60岁的市民300万人,问40~50岁年龄段的关注本次大会的人数约有多少?18. “一带一路”促进了中欧贸易的发展,我市某机电公司生产的 , 两种产品在欧洲市场热销.今年第一季度这两种产品的销售总额为2060万元,总利润为1020万元(利润=售价-成本).其每件产品的成本和售价信息如下表:
(1)、请直接写出 , , 第3组人数在扇形统计图中所对应的圆心角是度.(2)、请补全上面的频数分布直方图;(3)、假设该市现有10~60岁的市民300万人,问40~50岁年龄段的关注本次大会的人数约有多少?18. “一带一路”促进了中欧贸易的发展,我市某机电公司生产的 , 两种产品在欧洲市场热销.今年第一季度这两种产品的销售总额为2060万元,总利润为1020万元(利润=售价-成本).其每件产品的成本和售价信息如下表:成本(单位:万元/件)
2
4
售价(单位:万元/件)
5
7
问该公司这两种产品的销售件数分别是多少?
19. 如图,在 中, , 的平分线 交 于点 ,点 在 上,以 为直径的 经过点 . (1)、求证:① 是 的切线;
(1)、求证:① 是 的切线;② ;
(2)、若点 是劣弧 的中点,且 ,试求阴影部分的面积.20. 如图,正方形 和 的边 , 在同一条直线上,且 ,取 的中点 ,连接 , , .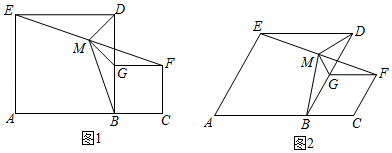 (1)、试证明 ,并求 的值.(2)、如图,将如图中的正方形变为菱形,设 ,其它条件不变,问(1)中 的值有变化吗?若有变化,求出该值(用含 的式子表示);若无变化,说明理由.21. 如图,顶点为 的抛物线 与 轴交于 , 两点,与 轴交于点 .
(1)、试证明 ,并求 的值.(2)、如图,将如图中的正方形变为菱形,设 ,其它条件不变,问(1)中 的值有变化吗?若有变化,求出该值(用含 的式子表示);若无变化,说明理由.21. 如图,顶点为 的抛物线 与 轴交于 , 两点,与 轴交于点 .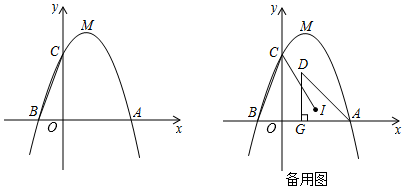 (1)、求这条抛物线对应的函数表达式;(2)、问在 轴上是否存在一点 ,使得 为直角三角形?若存在,求出点 的坐标;若不存在,说明理由.(3)、若在第一象限的抛物线下方有一动点 ,满足 ,过 作 轴于点 ,设 的内心为 ,试求 的最小值.
(1)、求这条抛物线对应的函数表达式;(2)、问在 轴上是否存在一点 ,使得 为直角三角形?若存在,求出点 的坐标;若不存在,说明理由.(3)、若在第一象限的抛物线下方有一动点 ,满足 ,过 作 轴于点 ,设 的内心为 ,试求 的最小值.