山东省威海市2019年中考数学试卷
试卷更新日期:2019-07-09 类型:中考真卷
一、单选题
-
1. -3的相反数是( )A、 -3 B、 C、 D、2. 据央视网报道,2019年1~4月份我国社会物流总额为88.9万亿元人民币,“88.9万亿”用科学记数法表示为( )A、 B、 C、 D、3. 如图,一个人从山脚下的 点出发,沿山坡小路 走到山顶 点.已知坡角为 ,山高 千米.用科学计算器计算小路 的长度,下列按键顺序正确的是( )
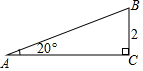 A、
A、 B、
B、 C、
C、 D、
D、 4. 如图所示的几何体是由几个大小相同的小正方体搭成的,其俯视图是( )
4. 如图所示的几何体是由几个大小相同的小正方体搭成的,其俯视图是( )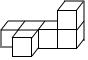 A、
A、 B、
B、 C、
C、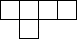 D、
D、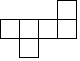 5. 下列运算正确的是( )A、 B、 C、 D、6. 为配合全科大阅读活动,学校团委对全校学生阅读兴趣调查的数据进行整理.欲反映学生感兴趣的各类图书所占百分比,最适合的统计图是( )A、条形统计图 B、频数直方图 C、折线统计图 D、扇形统计图7. 如图, 是 边 延长线上一点,连接 , , , 交 于点 .添加以下条件,不能判定四边形 BDEC 为平行四边形的是( )
5. 下列运算正确的是( )A、 B、 C、 D、6. 为配合全科大阅读活动,学校团委对全校学生阅读兴趣调查的数据进行整理.欲反映学生感兴趣的各类图书所占百分比,最适合的统计图是( )A、条形统计图 B、频数直方图 C、折线统计图 D、扇形统计图7. 如图, 是 边 延长线上一点,连接 , , , 交 于点 .添加以下条件,不能判定四边形 BDEC 为平行四边形的是( )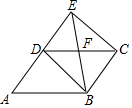 A、 B、 C、 D、8. 计算 的结果是( )A、 B、 C、 D、9. 解不等式组 时,不等式①②的解集在同一条数轴上表示正确的是( )A、
A、 B、 C、 D、8. 计算 的结果是( )A、 B、 C、 D、9. 解不等式组 时,不等式①②的解集在同一条数轴上表示正确的是( )A、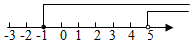 B、
B、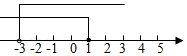 C、
C、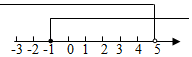 D、
D、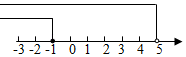 10. 已知 , 是方程 的两个实数根,则 的值是( )A、2023 B、2021 C、2020 D、201911. 甲、乙施工队分别从两端修一段长度为380米的公路.在施工过程中,乙队曾因技术改进而停工一天,之后加快了施工进度并与甲队共同按期完成了修路任务.下表是根据每天工程进度绘制而成的.
10. 已知 , 是方程 的两个实数根,则 的值是( )A、2023 B、2021 C、2020 D、201911. 甲、乙施工队分别从两端修一段长度为380米的公路.在施工过程中,乙队曾因技术改进而停工一天,之后加快了施工进度并与甲队共同按期完成了修路任务.下表是根据每天工程进度绘制而成的.施工时间/天
1
2
3
4
5
6
7
8
9
累计完成施工量/米
35
70
105
140
160
215
270
325
380
下列说法错误的是( )
A、甲队每天修路20米 B、乙队第一天修路15米 C、乙队技术改进后每天修路35米 D、前七天甲,乙两队修路长度相等12. 如图, 与x轴交于点 , ,与 轴的正半轴交于点 .若 ,则点 的纵坐标为( )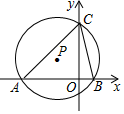 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
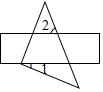
13. 把一块含有 角的直角三角板与两条长边平行的直尺如图放置(直角顶点在直尺的一条长边上).若 ,则 .
 14. 分解因式: .15. 如图,在四边形 中, ,过点 作 ,交 于点 ,连接 , ,若 ,则 .
14. 分解因式: .15. 如图,在四边形 中, ,过点 作 ,交 于点 ,连接 , ,若 ,则 . 16. 一元二次方程 的解是 .17. 如图,在四边形 中, ,连接 , .若 , , ,则 .
16. 一元二次方程 的解是 .17. 如图,在四边形 中, ,连接 , .若 , , ,则 .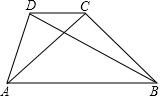
三、解答题
-
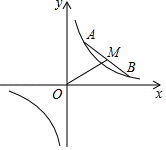
18. 如图,在平面直角坐标系中,点 , 在反比例函数 的图象上运动,且始终保持线段 的长度不变. 为线段 的中点,连接 .则线段 长度的最小值是(用含 的代数式表示).
 19. 列方程解应用题:
19. 列方程解应用题:小明和小刚约定周末到某体育公园打羽毛球.他们两家到体育公园的距离分别是1200米,3000米,小刚骑自行车的速度是小明步行速度的3倍,若二人同时到达,则小明需提前4分钟出发,求小明和小刚两人的速度.
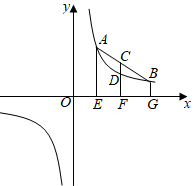
20. 在一个箱内装入只有标号不同的三颗小球,标号分别为1,2,3.每次随机取出一颗小球,记下标号作为得分,再将小球放回箱内.小明现已取球三次,得分分别为1分,3分,2分,小明又从箱内取球两次,若五次得分的平均数不小于2.2分,请用画树状图或列表的方法,求发生“五次取球得分的平均数不小于2.2分”情况的概率.21.(1)、阅读理解如图,点 , 在反比例函数 的图象上,连接 ,取线段 的中点 .分别过点 , , 作 轴的垂线,垂足为 , , , 交反比例函数 的图象于点 .点 , , 的横坐标分别为 , , .小红通过观察反比例函数 的图象,并运用几何知识得出结论:AE+BG=2CF,CF>DF,由此得出一个关于 , , 之间数量关系的命题:若 ,则 .
(2)、证明命题小东认为:可以通过“若 ,则 ”的思路证明上述命题.
小晴认为:可以通过“若 , ,且 ,则 ”的思路证明上述命题.
请你选择一种方法证明(1)中的命题.
 22. 如图是把一个装有货物的长方体形状的木箱沿着坡面装进汽车货厢的示意图.已知汽车货厢高度BG=2米,货厢底面距地面的高度BH=0.6米,坡面与地面的夹角 ,木箱的长( )为2米,高( )和宽都是1.6米.通过计算判断:当 ,木箱底部顶点 与坡面底部点 重合时,木箱上部顶点 会不会触碰到汽车货厢顶部.
22. 如图是把一个装有货物的长方体形状的木箱沿着坡面装进汽车货厢的示意图.已知汽车货厢高度BG=2米,货厢底面距地面的高度BH=0.6米,坡面与地面的夹角 ,木箱的长( )为2米,高( )和宽都是1.6米.通过计算判断:当 ,木箱底部顶点 与坡面底部点 重合时,木箱上部顶点 会不会触碰到汽车货厢顶部.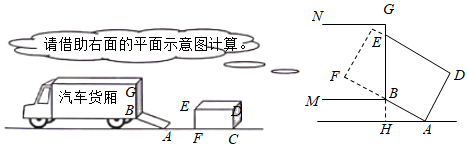 23. 在画二次函数 的图象时,甲写错了一次项的系数,列表如下
23. 在画二次函数 的图象时,甲写错了一次项的系数,列表如下……
﹣1
0
1
2
3
……
……
6
3
2
3
6
……
乙写错了常数项,列表如下:
……
﹣1
0
1
2
3
……
……
﹣2
﹣1
2
7
14
……
通过上述信息,解决以下问题:
(1)、求原二次函数 的表达式;(2)、对于二次函数 ,当 时, 的值随 的值增大而增大;(3)、若关于 的方程 有两个不相等的实数根,求 的取值范围.24. 如图,在正方形 中, , 为对角线 上一动点,连接 , ,过 点作 ,交直线 于点 . 点从 点出发,沿着 方向以每秒 的速度运动,当点 与点 重合时,运动停止.设 的面积为 , 点的运动时间为 秒.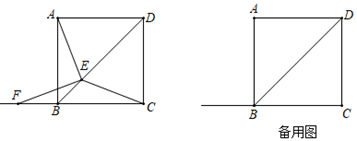 (1)、求证: ;(2)、求y与x之间关系的函数表达式,并写出自变量x的取值范围;(3)、求 面积的最大值.25.(1)、方法选择
(1)、求证: ;(2)、求y与x之间关系的函数表达式,并写出自变量x的取值范围;(3)、求 面积的最大值.25.(1)、方法选择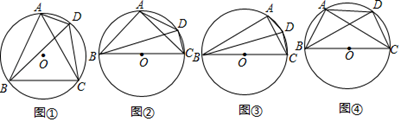
如图①,四边形 是 的内接四边形,连接 , , .求证: .
小颖认为可用截长法证明:在 上截取 ,连接 …
小军认为可用补短法证明:延长 至点 ,使得 …
请你选择一种方法证明.
(2)、类比探究(探究1)
如图②,四边形 是 的内接四边形,连接 , , 是 的直径, .试用等式表示线段 , , 之间的数量关系,并证明你的结论.
(探究2)
如图③,四边形 是 的内接四边形,连接 , .若 是 的直径, ,则线段 , , 之间的等量关系式.
(3)、拓展猜想如图④,四边形 是 的内接四边形,连接 , .若 是 的直径, ,则线段 , , 之间的等量关系式是 .