重庆市巴南区七校共同体2018-2019学年七年级下学期数学第三次月考试卷
试卷更新日期:2019-07-08 类型:月考试卷
一、单选题
-
1. 在-2, , ,3.14, , ,这6个数中,无理数共有( )A、4个 B、3个 C、2个 D、1个2. 下列运算正确的是( )A、 B、 C、 D、3. 如图,下列不能判定AB∥CD的条件是( )
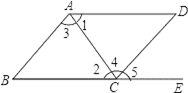 A、∠B+∠BCD=180° B、∠1=∠2 C、∠3=∠4 D、∠B=∠54. 已知P是直线l外一点, A,B,C是直线l上一点,且PA=5,PB=3,PC=2,那么点P到直线l的距离为( ).A、等于2 B、.大于2 C、小于或等于2 D、小于25. 方程组 的解是( )A、 B、 C、 D、6. 下列下列命题是真命题的是( )A、过一点有且只有一条直线与已知直线垂直 B、相等的两个角一定是对顶角 C、将一根细木条固定在墙上,只需要一根钉子 D、同角的余角相等7. 为保护生态环境,重庆市某县响应国家“退耕还林”号召,将某一部分耕地改为林地,改变后,林地面积和耕地面积共有180平方千米,耕地面积是林地面积的25%,求改变后林地面积和耕地面积各多少平方千米。设改变后耕地面积x平方千米,林地地面积y平方千米,根据题意,列出如下四个方程组,其中正确的是( )A、 B、 C、 D、8. 不等式 的正整数解有( ).A、1个 B、2个 C、3个 D、4个9. 满足-1<x≤2的数在数轴上表示为( ).A、
A、∠B+∠BCD=180° B、∠1=∠2 C、∠3=∠4 D、∠B=∠54. 已知P是直线l外一点, A,B,C是直线l上一点,且PA=5,PB=3,PC=2,那么点P到直线l的距离为( ).A、等于2 B、.大于2 C、小于或等于2 D、小于25. 方程组 的解是( )A、 B、 C、 D、6. 下列下列命题是真命题的是( )A、过一点有且只有一条直线与已知直线垂直 B、相等的两个角一定是对顶角 C、将一根细木条固定在墙上,只需要一根钉子 D、同角的余角相等7. 为保护生态环境,重庆市某县响应国家“退耕还林”号召,将某一部分耕地改为林地,改变后,林地面积和耕地面积共有180平方千米,耕地面积是林地面积的25%,求改变后林地面积和耕地面积各多少平方千米。设改变后耕地面积x平方千米,林地地面积y平方千米,根据题意,列出如下四个方程组,其中正确的是( )A、 B、 C、 D、8. 不等式 的正整数解有( ).A、1个 B、2个 C、3个 D、4个9. 满足-1<x≤2的数在数轴上表示为( ).A、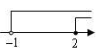 B、
B、 C、
C、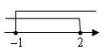 D、
D、 10. 下列是用火柴棒拼成的一组图形,第①个图形中有 3 根火柴棒,第②个图形中有 9 根火柴棒,第③个图形中有 18 根火柴棒,…,按此规律排列下去,第⑥个图形中火柴棒的根数是( ).
10. 下列是用火柴棒拼成的一组图形,第①个图形中有 3 根火柴棒,第②个图形中有 9 根火柴棒,第③个图形中有 18 根火柴棒,…,按此规律排列下去,第⑥个图形中火柴棒的根数是( ).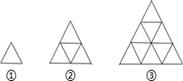 A、63 B、60 C、56 D、4511. 如图,已知四边形ABCD中,AB∥DC,连接 BD,BE 平分∠ABD,BE⊥AD,∠EBC 和∠DCB 的角平分线相交于点F,若∠ADC=110°,则∠F 的度数为( ).
A、63 B、60 C、56 D、4511. 如图,已知四边形ABCD中,AB∥DC,连接 BD,BE 平分∠ABD,BE⊥AD,∠EBC 和∠DCB 的角平分线相交于点F,若∠ADC=110°,则∠F 的度数为( ).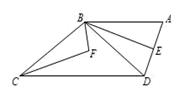 A、115° B、110° C、105° D、100°12. 已知关于x的不等式组 的整数解共有5个,则a的取值范围是( ).A、-4< a≤-3 B、-3<a≤-4 C、-4<a<-3 D、-3<a<-4
A、115° B、110° C、105° D、100°12. 已知关于x的不等式组 的整数解共有5个,则a的取值范围是( ).A、-4< a≤-3 B、-3<a≤-4 C、-4<a<-3 D、-3<a<-4二、解答题
-
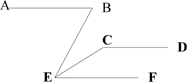
13. + - =.14. 如图,∠B=70°,∠BEF=70° ,∠DCE=140°, CD∥AB,求∠BEC的度数.
 15. 解方程(组)(1)、4(x+1)2 =81(2)、16. 解不等式(组)(1)、2(x+5)≤3(x+4),并写出非正整数解(2)、 ,并在数轴上表示解集17. 如图,三角形ABC在平面直角坐标系中,完成下列问题:
15. 解方程(组)(1)、4(x+1)2 =81(2)、16. 解不等式(组)(1)、2(x+5)≤3(x+4),并写出非正整数解(2)、 ,并在数轴上表示解集17. 如图,三角形ABC在平面直角坐标系中,完成下列问题: (1)、请写出三角形ABC各顶点的坐标;(2)、求出三角形ABC的面积;(3)、若把三角形ABC向上平移2个单位,在向右平移2个单位得到三角形A´B´C´,在图中画出平移以后的图形,并写出顶点A´、B´、C´的坐标.18. 某水果店以4元/千克的价格购进一批水果,由于销售状况良好,该店又再次购进同一种水果,第二次进货价格比第一次每千克便宜了0.5元,所购水果重量恰好是第一次购进水果重量的2倍,这样该水果店两次购进水果共花去了2200元.(1)、该水果店两次分别购买了多少元的水果?(2)、在销售中,尽管两次进货的价格不同,但水果店仍以相同的价格售出,若第一次购进的水果有3% 的损耗,第二次购进的水果有5% 的损耗,该水果店希望售完这些水果获利不低于1244元,则该水果每千克售价至少为多少元?19. 如图,AD平分∠BAC交BC于点D,点F在BA的延长线上,点E在线段CD上,EF 与AC相交于点G,∠BDA+∠CEG=180°.
(1)、请写出三角形ABC各顶点的坐标;(2)、求出三角形ABC的面积;(3)、若把三角形ABC向上平移2个单位,在向右平移2个单位得到三角形A´B´C´,在图中画出平移以后的图形,并写出顶点A´、B´、C´的坐标.18. 某水果店以4元/千克的价格购进一批水果,由于销售状况良好,该店又再次购进同一种水果,第二次进货价格比第一次每千克便宜了0.5元,所购水果重量恰好是第一次购进水果重量的2倍,这样该水果店两次购进水果共花去了2200元.(1)、该水果店两次分别购买了多少元的水果?(2)、在销售中,尽管两次进货的价格不同,但水果店仍以相同的价格售出,若第一次购进的水果有3% 的损耗,第二次购进的水果有5% 的损耗,该水果店希望售完这些水果获利不低于1244元,则该水果每千克售价至少为多少元?19. 如图,AD平分∠BAC交BC于点D,点F在BA的延长线上,点E在线段CD上,EF 与AC相交于点G,∠BDA+∠CEG=180°.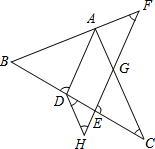 (1)、AD与EF平行吗?请说明理由;(2)、若点H在FE的延长线上,且∠EDH=∠C,若∠F=40°,求∠H的度数.20. 如图,在下面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a、b、c满足关系式 +(b﹣3)2=0,(c﹣4)2≤0.
(1)、AD与EF平行吗?请说明理由;(2)、若点H在FE的延长线上,且∠EDH=∠C,若∠F=40°,求∠H的度数.20. 如图,在下面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a、b、c满足关系式 +(b﹣3)2=0,(c﹣4)2≤0.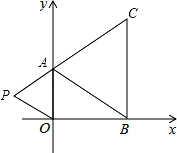 (1)、a=、b=、c=;(2)、求四边形AOBC的面积;(3)、如果在第二象限内有一点P(m, ),且四边形ABOP的面积与△ABC的面积相等 ,求出点P的坐标.21. 如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.
(1)、a=、b=、c=;(2)、求四边形AOBC的面积;(3)、如果在第二象限内有一点P(m, ),且四边形ABOP的面积与△ABC的面积相等 ,求出点P的坐标.21. 如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.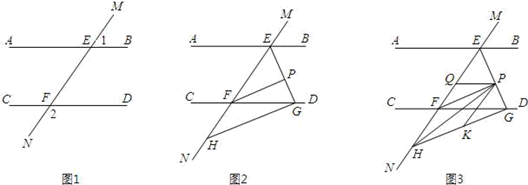 (1)、试判断直线AB与直线CD的位置关系,并说明理由;(2)、如图2,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上一点,且GH⊥EG,求证:PF∥GH;(3)、如图3,在(2)的条件下,连接PH,K是GH上一点使∠PHK=∠HPK,作PQ平分∠EPK,问∠HPQ的大小是否发生变化?若不变,请求出其值;若变化,说明理由.
(1)、试判断直线AB与直线CD的位置关系,并说明理由;(2)、如图2,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上一点,且GH⊥EG,求证:PF∥GH;(3)、如图3,在(2)的条件下,连接PH,K是GH上一点使∠PHK=∠HPK,作PQ平分∠EPK,问∠HPQ的大小是否发生变化?若不变,请求出其值;若变化,说明理由.三、填空题

