辽宁省大连市民间优质校联盟2018-2019学年七年级下学期数学4月月考试卷

试卷更新日期：2019-07-08 类型：月考试卷

进入 出卷网 下载

一、单选题

  • 1. 下列各图中，∠1与∠2是对顶角的是（   ）
    A、 B、 C、 D、

    查看试题解析

  • 2. 在平面直角坐标系中，点A（20，﹣20）在（   ）
    A、第一象限 B、第二象限 C、第三象限 D、第四象限

    查看试题解析

  • 3. 下列实数是无理数的是（   ）
    A、﹣2 B、π C、13 D、16

    查看试题解析

  • 4. 已知：如图，直线BO⊥AO于点O，OB平分∠COD，∠BOD＝22°．则∠AOC的度数是（ ）

    A、22° B、46° C、68° D、78°

    查看试题解析

  • 5. 9的平方根是（ ）
    A、3 B、81 C、±3 D、±81

    查看试题解析

  • 6. 把点 A(−2 ， 1) 向下平移2个单位后得到点B，则点B的坐标是 (    )
    A、(−2 ， 3) B、(−2 ， −1) C、(0 ， 1) D、(−4 ， 1)

    查看试题解析

  • 7. 如图，∠1＝65°，CD∥EB，则∠B的度数为（   ）

    A、32° B、68° C、115° D、125°

    查看试题解析

  • 8. 如图所示，某同学的家在P处，他想尽快赶到附近公路边搭公交车，他选择P→C路线，用几何知识解释其道理正确的是（   ）

    A、两点确定一条直线 B、垂直线段最短 C、两点之间线段最短 D、三角形两边之和大于第三边

    查看试题解析

  • 9. 如图，在一次“寻宝”游戏中，寻宝人找到了如图所示的两个标志点A（3，1），B（2，2），则“宝藏”点C的位置是（   ）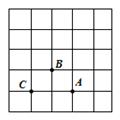

    A、（1，0） B、（1，2） C、（2，1） D、（1，1）

    查看试题解析

  • 10. 若2m﹣4与3m﹣1是同一个数的平方根，则这个数可能是（   ）
    A、2 B、﹣2 C、4 D、1

    查看试题解析

二、填空题

  • 11. 0.0273 = ．

    查看试题解析

  • 12. 比较大小： 6 3(填：“>”或“<”或“=”)

    查看试题解析

  • 13. 若点M(a﹣3，a+1)在y轴上，则M点的坐标为 ．

    查看试题解析

  • 14. 如图，小明在平面直角坐标系中先作边长为1的正方形OABC ， 再用圆规以A为圆心，AC为半径画弧交x轴正半轴于点P ， 则点P的坐标为 ．

    查看试题解析

  • 15. 在平面直角坐标系中，点M在x轴的上方，y轴的左面，且点M到x轴的距离为4，到y轴的距离为7，则点M的坐标是 ．

    查看试题解析

  • 16. 如图，请你添加一个条件使得DE∥AB.

    查看试题解析

三、解答题

  • 17. 求出下列x的值：
    (1)、4x2﹣81＝0；
    (2)、8（x+1）3＝27．

    查看试题解析

  • 18. 如图，OA⊥OC ， OB⊥OD ．

    (1)、∠AOD与∠BOC相等吗？为什么？
    (2)、已知∠AOB＝140°，求∠COD的度数．

    查看试题解析

  • 19. 如图，∠DAB+∠D＝180°，AC平分∠DAB ， 且∠CAD＝25°，求∠C的度数．

    查看试题解析

  • 20. 如图，已知△ABC经过平移后得到△DEF ， 点A与点D ， 点B与点E ， 点C与点F分别是对应点，已知点A（3，3）、D（-2，1），解答下列问题：

    (1)、请在坐标系中画出平移后的△DEF；
    (2)、请直接写出以下点的坐标：B（ ， ）、C（ ， ）、E（ ， ）、F（ ， ）；
    (3)、若点P（x ， y）通过上述的平移规律平移得到的对应点为Q（3，5），则P点坐标为（ ， ）．

    查看试题解析

  • 21. 已知平面直角坐标系中有一点 M(2m−3,m+1) .
    (1)、点M到y轴的距离为1时，M的坐标？
    (2)、点 N(5,−1) 且MN//x轴时，M的坐标？

    查看试题解析

  • 22. 如图，四边形ABCD中，AD∥BC ， F为AB边上一点，且∠ADF=∠CDB ， 射线DF、CB相交于点E ， ∠BFE=∠CBD ． 求证：AB∥CD.

    查看试题解析

  • 23. 如图，长方形OABC中，O为平面直角坐标系的原点，A点的坐标为（4，0），C点的坐标为（0，3），点B在第一象限内，点P从原点出发，以每秒2个单位长度的速度沿着O﹣C﹣B﹣A﹣O的路线移动（即：沿着长方形移动一周）．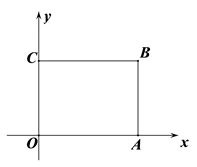

    (1)、直接写出B点的坐标；
    (2)、当点P移动了3秒时，请直接写出点P的坐标；
    (3)、在移动过程中，当点P到x轴距离为2个单位长度时，求点P移动的时间．

    查看试题解析

  • 24. 先填写表，通过观察后再回答问题：

    a

    0

    0.0001

    0.01

    1

    100

    10000

    …

        a

    0

    0.01

    x

    1

    y

    100

    …
    (1)、表格中x＝ ， y＝；
    (2)、从表格中探究a与 a 数位变化可以发现：当被开方数a每扩大100倍时， a 扩大倍，请你利用这个规律解决下面两个问题：

    ①已知 6≈2.45 ，则 600≈ ；

    ②已 m≈3.16 ，若 n≈316 ，用含m的代数式表示n ， 则n＝；

    (3)、请根据表格提示，试比较 a 与a的大小．

    查看试题解析

  • 25. 阅读下面材料：

    小明遇到这样一个问题：

          

    (1)、如图1，AC∥BD ， 点E为直线AC上方一点，连接CE、DE ， 猜想∠C、∠D、∠E的数量关系，并证明.
    (2)、用学过的知识或参考小明的方法，解决下面的问题：

    如图3，AB∥CD ， P是平面内一点，连接AP、CP ， 使AP∥BD ， ∠APC=100°，BM、CM分别平分∠ABD ， ∠DCP交于点M ， 求∠M的度数．

    查看试题解析

  • 26. 平面直角坐标系中，A（m ， 0）、B（m+1，0）、E（2，0），其中-1≤m≤2，分别以AB、OE为边向上作正方形ABCD、OEFG.
    (1)、请直接写出线段AB的长；
    (2)、正方形ABCD沿x轴正半轴运动过程中与正方形OEFG重叠部分面积为S ， 求S与m的关系式.

    查看试题解析