辽宁省大连市民间优质校联盟2018-2019学年八年级下学期数学4月月考试卷

试卷更新日期：2019-07-08 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列各式一定是二次根式的是（）

A、 $\sqrt{a}$ B、 $\sqrt{5 a - 1}$ C、 $\sqrt{3 a + 2}$ D、 $\sqrt{a^{2} + 4}$

查看试题解析
2. 与 $\sqrt{3}$ 是同类二次根式的是（）

A、 $\sqrt{12}$ B、 $\sqrt{13}$ C、 $\sqrt{24}$ D、 $\sqrt{30}$

查看试题解析
3. 如图，正方形A，B，C的边长分别为直角三角形的三边长，若正方形A，B的边长分别为3和5，则正方形C的面积为（）

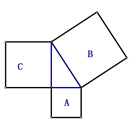A、4 B、15 C、16 D、18

查看试题解析
4. 如图，在平行四边形ABCD中，∠A：∠B＝3：2，则∠D的度数为（）

A、60 B、72° C、80° D、108°

查看试题解析
5. 下列哪个是最简二次根式（）

A、 $\sqrt{8}$ B、 $\sqrt{16}$ C、 $\sqrt{18}$ D、 $\sqrt{21}$

查看试题解析
6. 下列各组数中，能作为直角三角形的三边长的是（）

A、2，4，5 B、3，4，6 C、6，8，10 D、9，16，25

查看试题解析
7. 如果 $\sqrt{{(3 a - 2)}^{2}} = 3 a - 2$ ，那么a的取值范围（）

A、 $a > \frac{2}{3}$ B、 $a < \frac{2}{3}$ C、 $a \geq \frac{2}{3}$ D、 $a \leq \frac{2}{3}$

查看试题解析
8. 如图，在四边形ABCD中，给出下列的条件，能判断它是平行四边形的是（）

A、AB//CD， AD=BC B、∠B＝∠C，∠A＝∠D C、AB=AD， BC=CD D、AB=CD， AD=BC

查看试题解析
9. 已知 $(3 + \sqrt{5}) \cdot a = b$ ，若b是整数，则a的值可能是（）

A、 $\sqrt{5}$ B、 $3 - \sqrt{5}$ C、 $3 + \sqrt{5}$ D、 $2 - \sqrt{5}$

查看试题解析
10. 如图，甲同学从A地沿北偏西60°方向走100m到B地，再从B地向正南方向走200m到C地，此时甲同学离A地（）

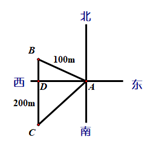A、 $50 \sqrt{3}$ m B、100m C、150m D、 $100 \sqrt{3}$ m

查看试题解析

二、填空题

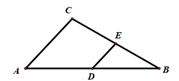
11. 如图，在△ABC中，点D，E分别是边AB，BC的中点，若DE的长是3，则AC的长为.

查看试题解析
12. 计算： $\frac{\sqrt{5}}{\sqrt{3}}$ ＝.

查看试题解析
13. 如图，在等腰△ABC中，底边BC=16，底边上的高AD=6，则腰AB=.

查看试题解析
14. 矩形的长和宽分别是 $\sqrt{15}$ 和 $\sqrt{5}$ ，则矩形的面积为.

查看试题解析
15. 如图，在平行四边形ABCD中，BC＝10，AC＝8，BD＝14，△AOD的周长是.

查看试题解析
16. 如图，有一个长方体的盒子，它的长、宽、高分别是4m，3m和12m，则盒内可放的木棒最长为m.

查看试题解析

三、解答题

17. 如图，在四边形ABCD中，∠A＝90°，AB＝3，AD＝4，BC＝12，CD＝13.求证：BD⊥CB.

查看试题解析
18. 如图，在平行四边形ABCD中，E、F分别为BC、AD上的点，且∠1＝∠2.求证：AF＝CE.

查看试题解析
19. 如图，在Rt△ABC中，∠C＝90°，a＋b＝14，C＝10，求Rt△ABC的面积.

查看试题解析
20.

(1)、 $\sqrt{8} + 2 \sqrt{3} - (\sqrt{27} - \sqrt{2})$

(2)、 $(2 \sqrt{5} - 5 \sqrt{2}) (- 2 \sqrt{5} - 5 \sqrt{2}) - {(\sqrt{5} - \sqrt{2})}^{2}$

查看试题解析
21. 由于大风，山坡上的一棵树甲被从点A处拦腰折断，如图，其树恰好落在另一棵树乙的根部C处，已知AB=1米，BC=5米，已知两棵树的水平距离为3米，请计算出这棵树原来的高度（结果保留根号）

查看试题解析
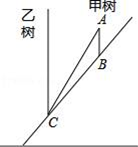22. 已知矩形的周长为 $(\sqrt{48} + \sqrt{72}) c m$ ，一边长为 $(\sqrt{3} + \sqrt{12}) c m$ ，求此矩形的另一边长和它的面积？

查看试题解析
23. 如图，在平行四边形ABCD中，点E、F在AC上，且AF＝CE，点G、H分别在AB、CD上，且AG＝CH，AC与GH相交于点O.

(1)、求证：EG//FH；

(2)、GH、EF互相平分.

查看试题解析
24. 小明在解方程 $\sqrt{24 - x} - \sqrt{8 - x} = 2$ 时运用了下面的方法：由 $(\sqrt{24 - x} - \sqrt{8 - x}) (\sqrt{24 - x} + \sqrt{8 - x}) = {(\sqrt{24 - x})}^{2} - {(\sqrt{8 - x})}^{2} = (24 - x) - (8 - x) = 16$ ，又由 $\sqrt{24 - x} - \sqrt{8 - x} = 2$ 可得 $\sqrt{24 - x} + \sqrt{8 - x} = 8$ ，将这两式相加可得 $\sqrt{24 - x} = 5$ ，将 $\sqrt{24 - x} = 5$ 两边平方可解得 $x$ ＝－1，经检验 $x$ ＝－1是原方程的解.
请你参考小明的方法，解下列方程：

(1)、 $\sqrt{x^{2} + 42} + \sqrt{x^{2} + 10} = 16;$

(2)、 $\sqrt{4 x^{2} + 6 x - 5} + \sqrt{4 x^{2} - 2 x - 5} = 4 x$ .

查看试题解析
25. 如图，直线AB与x轴交于点A（4，0），与y轴交于点B（0，－4），若点E在线段AB上，OE⊥OF，且OE＝OF，连接AF.

(1)、猜想线段AF与BE之间的关系，并证明；

(2)、过点O作OM⊥EF垂足为D，OM分别交AF、BA的延长线于点C、M若BE= $3 \sqrt{2}$ ，求CF的长.

查看试题解析
26. 如图，等边△ABC的边长为8，动点M从点B出发，沿B→A→C→B的方向以每秒3个单位长度的速度运动，动点N从点C出发，沿C→A→B－C的方向以每秒2个单位长度的速度运动.

(1)、若动点M、N同时出发，经过几秒第一次相遇？

(2)、若动点M、N同时出发，且其中一点到达终点时，另一点即停止运动.在△ABC的边上是否存在一点D，使得以点A、M、N、D为顶点的四边形为平行四边形？若存在，求此时运动的时间 $t$ 及点D的具体位置；若不存在，请说明理由.

查看试题解析