江苏省扬州市江都区邵樊片2018-2019学年八年级下学期数学第二次月考试卷

试卷更新日期：2019-07-08 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列标志图中，既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列调查中，最适合采用抽样调查的是（）

A、对某地区现有的16名百岁以上老人睡眠时间的调查 B、对“神舟十一号”运载火箭发射前零部件质量情况的调查 C、对某校九年级三班学生视力情况的调查 D、对某市场上某一品牌电脑使用寿命的调查

查看试题解析
3. 不透明的袋子中装有形状、大小、质地完全相同的6个球，其中4个黑球、2个白球，从袋子中一次摸出3个球，下列事件是不可能事件的是（）

A、摸出的是3个白球 B、摸出的是3个黑球 C、摸出的是2个白球、1个黑球 D、摸出的是2个黑球、1个白球

查看试题解析
4. 如图，在▱ ABCD中，AB=3，BC=5，∠ABC的平分线交AD于点E，则DE的长为（）

A、5 B、4 C、3 D、2

查看试题解析
5. 分式 $\frac{2 x^{2}}{3 x - 2 y}$ 中的x、y同时扩大2倍，则分式值（）

A、不变 B、是原来的2倍 C、是原来的4倍 D、是原来的 $\frac{1}{2}$

查看试题解析
6. 若 $M (- \frac{1}{2} ， y_{1})$ 、 $N (- \frac{1}{4} ， y_{2})$ 、 $P (\frac{1}{2} ， y_{3})$ 三点都在函数 $y = \frac{k}{x} (k > 0)$ 的图象上，则 $y_{1}$ 、 $y_{2}$ 、 $y_{3}$ 的大小关系是（）

A、 $y_{2} > y_{3} > y_{1}$ B、 $y_{2} > y_{1} > y_{3}$ C、 $y_{3} > y_{1} > y_{2}$ D、 $y_{3} > y_{2} > y_{1}$

查看试题解析
7. 下列四个分式中，是最简分式的是（）

A、 $\frac{a^{2} + b^{2}}{a + b}$ B、 $\frac{x^{2} + 2 x + 1}{x + 1}$ C、 $\frac{2 a x}{3 a y}$ D、 $\frac{a^{2} - b^{2}}{a - b}$

查看试题解析
8. 如图，点P是矩形ABCD的边AD上的一动点，矩形的两条边AB，BC的长分别是6和8，则点P到矩形的两条对角线AC和BD的距离之和是（）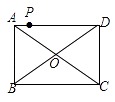

A、4.8 B、5 C、6 D、7.2

查看试题解析

二、填空题

9. 计算 $\sqrt{{(- 3)}^{2}}$ 的结果是.

查看试题解析
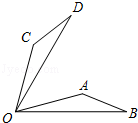
10. 将一批100个数据分成5组，列出分布表，其中第一组与第五组的频率之和是 $0.25$ ，第二与第四组的频率之和是 $0.54$ ，那么第三组的频数是.

查看试题解析
11. 如图，将△AOB绕点O按逆时针方向旋转45°后得到△COD，若∠AOB=15°，则∠AOD=度．

查看试题解析
12. 顺次连接矩形四条边的中点，所得到的四边形一定是形.

查看试题解析
13. 关于x的方程 $\frac{2 x + a}{x - 1} = 1$ 的解是正数，则a的取值范围是．

查看试题解析
14. 已知y＝(a－1) $x^{a^{2} - 2}$ 是反比例函数，则a＝.

查看试题解析
15.
在数轴上表示实数a的点如图所示，化简 $\sqrt{{(a - 5)}^{2}}$ ＋|a－2|的结果为．

查看试题解析
16. 对于任意不相等的两个数a，b，定义一种运算如下：如 $a * b = \frac{\sqrt{a + b}}{a - b}$ ， $3 * 2 = \frac{\sqrt{3 + 2}}{3 - 2}$ ，那么 $8 * 4$ =.

查看试题解析
17. 如图，在平面直角坐标系中，菱形OABC的面积为12，点B在y轴上，点C在反比例函数y= $\frac{k}{x}$ 的图象上，则k的值为.

查看试题解析
18. 如图以直角三角形ABC的斜边BC为边在三角形ABC的同侧作正方形BCEF，设正方形的中心为O，连结AO，如果AB=4，AO=6 $\sqrt{2}$ ，则AC=

查看试题解析

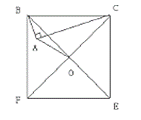
三、解答题

19. 计算：

(1)、 $(1 - \frac{1}{1 - x}) \div \frac{x}{x - 1} .$

(2)、 $\sqrt{5} \times \sqrt{\frac{5}{4}} \div \sqrt{\frac{4}{9}} .$

查看试题解析
20. 解下列分式方程：

(1)、 $\frac{2}{x + 1} + \frac{3}{x - 1} = \frac{6}{x^{2} - 1}$

(2)、 $\frac{1}{x - 2} + \frac{2 x}{2 - x} = 2$ ．

查看试题解析
21. 先化简( $\frac{3}{a + 1}$ －a＋1)÷ $\frac{a^{2} - 4 a + 4}{a + 1}$ ，并从0，－1，2中选一个合适的数作为a的值代入求值.

查看试题解析
22. 若x，y是实数，且 $y > \sqrt{x - 1} + \sqrt{1 - x} + 3$ ，求 $\frac{| 2 - y |}{y - 2}$ 的值.

查看试题解析
23. 某校为了开阔学生的视野，积极组织学生参加课外读书活动.“放飞梦想”读书小组协助老师随机抽取本校的部分学生，调查他们最喜爱的图书类别（图书分为文学类、艺体类、科普类、其他等四类），并将调查结果绘制成如下两幅不完整的统计图，请你结合图中的信息解答下列问题：

(1)、求被调查的学生人数；

(2)、补全条形统计图；

(3)、已知该校有1200名学生，估计全校最喜爱文学类图书的学生有多少人？

查看试题解析
24. 如图，在平行四边形ABCD中， $A E ⊥ B D$ ， $C F ⊥ B D$ ，垂足分别为E、 $F .$ 求证：

(1)、 $A E = C F$ ；

(2)、四边形AECF是平行四边形.

查看试题解析
25. 某商店准备购进一批电冰箱和空调，每台电冰箱的进价比每台空调的进价多400元，商店用8000元购进电冰箱的数量与用6400元购进空调的数量相等.求每台电冰箱与空调的进价分别是多少？

查看试题解析
26. 如图，反比例函数 $y_{1} = \frac{m}{x}$ 的图像与一次函数 $y_{2} = k x + b$ 的图像交于A、B两点.已知A (2，n），B（ $- \frac{1}{2}$ ， $- 2$ ）.

(1)、求反比例函数和一次函数的解析式；

(2)、求△AOB的面积；

(3)、请结合图像直接写出当y₁≥y₂时自变量x的取值范围.

查看试题解析
27. 如图，点P是函数y $= \frac{2}{x}$ 上第一象限上一个动点，点A的坐标为（0，1），点B的坐标为（1，0）.

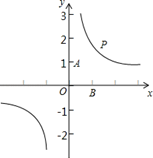(1)、连结PA、PB、AB，设△PAB的面积为S，点P的横坐标为t.请写出S关于t的函数关系式，并指出自变量t的取值范围；

(2)、阅读下面的材料回答问题
阅读材料：当a>0时， $a + \frac{1}{a} = {(\sqrt{a})}^{2} - 2 + {(\frac{1}{\sqrt{a}})}^{2} + 2 = {(\sqrt{a} - \frac{1}{\sqrt{a}})}^{2} + 2 \geq 2$

因为 ${(\sqrt{a} - \frac{1}{\sqrt{a}})}^{2} \geq 0 ，$ 当 $\sqrt{a} = \frac{1}{\sqrt{a}}$ ，即a=1时， ${(\sqrt{a} - \frac{1}{\sqrt{a}})}^{2} = 0 ，$

所以a=1时， $a + \frac{1}{a}$ 有最小值为2.

根据上述材料在（1）中研究当t为何值时△PAB的面积S有最小值，并求出S的最小值.

查看试题解析
28. 在平行四边形ABCD中，∠BAD的平分线交线段BC于点E，交线段DC的延长线于点F，以EC、CF为邻边作平行四边形ECFG.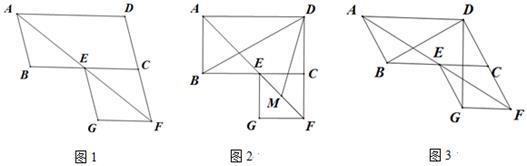

(1)、如图1，证明平行四边形ECFG为菱形；

(2)、如图2，若∠ABC=90°，M是EF的中点，求∠BDM的度数；

(3)、如图3，若∠ABC=120°，请直接写出∠BDG的度数.

查看试题解析