江苏省江阴市华士片2018-2019学年八年级下学期数学5月月考试卷

试卷更新日期：2019-07-08 类型：月考试卷

进入出卷网下载

一、单选题

1. 随着我国经济快速发展，轿车进入百姓家庭，下列汽车标志，其中是中心对称图案的是（）

A、 B、 C、 D、

查看试题解析
2. 下列根式中属最简二次根式的是（）

A、 $\sqrt{a^{2} + 1}$ B、 $\sqrt{\frac{1}{2}}$ C、 $\sqrt{8}$ D、 $\frac{1}{\sqrt{2}}$

查看试题解析
3. 下列事件中，是必然事件的为（）

A、3天内会下雨 B、打开电视，正在播放广告 C、367人中至少有2人公历生日相同 D、某妇产医院里，下一个出生的婴儿是女孩

查看试题解析
4. 若点（3，4）是反比例函数 $y = \frac{m^{2} + 2 m + 1}{x}$ 图象上一点，则此函数图象必须经过点（）

A、（3，﹣4） B、（2，﹣6） C、（4，﹣3） D、（2，6）

查看试题解析
5. 已知P₁（x₁ ， y₁），P₂（x₂ ， y₂），P₃（x₃ ， y₃）是反比例函数y= $\frac{6}{x}$ 的图象上三点，且y₁＜y₂＜0＜y₃ ，则x₁ ， x₂ ， x₃的大小关系是（）

A、x₁＜x₂＜x₃ B、x₃＜x₂＜x₁ C、x₂＜x₁＜x₃ D、x₂＜x₃＜x₁

查看试题解析
6. 如果把分式 $\frac{2 n}{m^{2} - n^{2}}$ 中的m和n都扩大2倍，那么分式的值（）

A、不变 B、扩大2倍 C、缩小2倍 D、扩大4倍

查看试题解析
7.
如图，点A是反比例函数y= $\frac{k}{x}$ 的图象上的一点，过点A作AB⊥x轴，垂足为B．点C为y轴上的一点，连接AC，BC．若△ABC的面积为3，则k的值是（　　）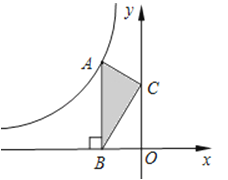

A、3 B、﹣3 C、6 D、﹣6

查看试题解析
8. 如图直线 y=kx(k<0) 与双曲线 $y = - \frac{2}{x}$ 交于 $A (x_{1} ， y_{1})$ ， $B (x_{2} ， y_{2})$ 两点，则 $3 x_{1} y_{2} - 8 x_{2} y_{1}$ 的值（）

A、-5 B、-10 C、5 D、10

查看试题解析
9. 已知函数y₁＝x（x＞0）， y₂＝ $\frac{9}{x}$ （x＞0）的图象如图，有下列结论：①两函数图象的交点A的坐标为（3，3 )；② 当x＞3时，y₂＞y₁ ；③BC = 4；④当x逐渐增大时，y₁随着x的增大而增大，y₂随着x 的增大而减小.其中正确的结论有（）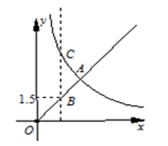

A、①③ B、①④ C、①②③ D、①③④

查看试题解析
10. 如图，边长为2a的等边△ABC中，M是高CH所在直线上的一个动点，连接MB，将线段BM绕点B逆时针旋转60°得到BN，连接HN.则在点M运动过程中，线段HN长度的最小值是（）

A、 $\frac{1}{2} a$ B、a C、 $\frac{\sqrt{3}}{2} a$ D、 $\sqrt{3} a$

查看试题解析

二、填空题

11. 当x时，分式 $\frac{x + 1}{2 x - 1}$ 有意义．

查看试题解析
12. 当 $m$ =时，函数 $y = (m - 1) x^{m^{2} - 2}$ 是反比例函数.

查看试题解析
13. 在菱形ABCD中，对角线AC＝6，BD＝8，则菱形ABCD的面积为.

查看试题解析
14. 设反比例函数y= $- \frac{2}{x}$ 的图象与一次函数y=-x+3的图象交于点（a，b），则 $\frac{1}{a} + \frac{1}{b}$ =.

查看试题解析
15. 关于x的方程 $\frac{2 x + a}{x - 1} = 3$ 的解是正数，则 $a$ 的取值范围是.

查看试题解析
16. 如图，点O是矩形ABCD的对角线AC的中点，OM∥AB交AD于点M，若OM=3，BC=10，则OB的长为.

查看试题解析
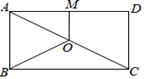17. 如图，等腰直角△ABC位于第二象限，BC＝AC＝3，直角顶点C在直线y＝﹣x上，且点C的横坐标为﹣4，边BC、AC分别平行于x轴、y轴.若双曲线y＝ $\frac{k}{x}$ 与△ABC的边AB有2个公共点，则k的取值范围为。

查看试题解析
18. 如图，在平面直角坐标系中，函数 $y = \frac{k}{x}$ (x＞0，常数k＞0)的图象经过点A(1，2)、B(m，n)(m＞1)．过点B作y轴的垂线，垂足为C若△ABC的面积为2，则点B的坐标为．

查看试题解析

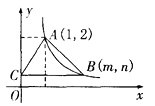
三、解答题

19. 计算或化简：

(1)、 $\sqrt{6} \times \frac{\sqrt{3}}{3} - {(\frac{1}{2})}^{- 2} + | 1 - \sqrt{2} |$

(2)、 $\frac{1}{m - 2} - \frac{4}{m^{2} - 4}$

查看试题解析
20. 解方程

(1)、 $\frac{1}{x - 3} - \frac{6 - x}{3 - x} = - 2$

(2)、x²﹣6x﹣4=0（用配方法）

查看试题解析
21. 已知：如图，在▱ABCD中，E，F两点在对角线BD上，且BE=DF.

(1)、求证：AE=CF；

(2)、当四边形AECF为矩形时，求 $\frac{B D - A C}{B E}$ 的值.

查看试题解析
22. 今年4月23日是第23个“世界读书日”.某校围绕学生日人均阅读时间这一问题，对初二学生进行随机抽样调查.如图是根据调查结果绘制成的统计图（不完整），请你根据图中提供的信息解答下列问题：

(1)、本次抽样调查的样本容量是。

(2)、请将条形统计图补充完整.

(3)、在扇形统计图中，计算出日人均阅读时间在1～1.5小时对应的圆心角是度.

(4)、根据本次抽样调查，试估计我市12000名初二学生中日均阅读时间在0.5～1.5小时的有多少人.

查看试题解析
23. 如图所示的正方形网格中，△ABC的顶点均在格点上，在所给直角坐标系中解答下列问题：

(1)、分别写出点A的坐标，点B的坐标.

(2)、作出△ABC关于原点成中心对称的△A₁B₁C₁；

(3)、已知点M的坐标为（1，﹣4），请你在x轴上找一点P，使得PM+PB的值最小，并直接写出点P的坐标.

查看试题解析
24. 如图，在平面直角坐标系xOy中，已知四边形DOBC是矩形，且D（0，4），B（6，0）.若反比例函数 $y_{1} = \frac{k_{1}}{x}$ （x＞0）的图象经过线段OC的中点A，交DC于点E，交BC于点F.设直线EF的解析式为y₂=k₂x+b.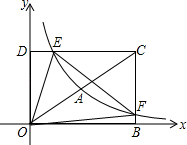

(1)、求反比例函数和直线EF的解析式；
（温馨提示：平面上有任意两点M（x₁ ， y₁）、N（x₂ ， y₂），它们连线的中点P的坐标为（ $\frac{x_{1} + x_{2}}{2} ， \frac{y_{1} + y_{2}}{2}$ ））

(2)、求△OEF的面积；

(3)、请结合图象直接写出不等式k₂x -b﹣ $\frac{k_{1}}{x}$ ＞0的解集.

查看试题解析
25. 在平面直角坐标系中，O为坐标原点，B在x轴上，四边形OACB为平行四边形，且∠AOB=60°，反比例函数 $y = \frac{k}{x}$ （k＞0）在第一象限内过点A，且与BC交于点F.

(1)、若OA=10，求反比例函数的解析式；

(2)、若F为BC的中点，且S△AOF＝24 $\sqrt{3}$ ，求OA长及点C坐标；

(3)、在（2）的条件下，过点F作EF∥OB交OA于点E（如图2），若点P是直线EF上一个动点，连结，PA，PO，问是否存在点P，使得以P，A，O三点构成的三角形是直角三角形？若存在，请直接写出P点坐标；若不存在，请说明了理由.

查看试题解析