江苏省灌云县西片2018-2019学年八年级下学期数学第二次月考试卷

试卷更新日期：2019-07-08 类型：月考试卷

进入出卷网下载

一、单选题

1. 若代数式 $\frac{x}{x - 4}$ 有意义，则实数 $x$ 的取值范围是（）

A、 $x \neq 4$ B、 $x = 4$ C、 $x \neq 0$ D、 $x = 0$

查看试题解析
2. 下列各式中，属于分式的是（）

A、a﹣6 B、 $\frac{m}{π}$ C、 $\frac{3}{n}$ D、 $\frac{3}{4}$ （x+y）

查看试题解析
3. 下列各式中，从左到右变形正确的是（）

A、 $\frac{a^{2} + b^{2}}{a + b}$ ＝a+b B、 $\frac{b}{a} = \frac{b^{2}}{a^{2}}$ C、 $\frac{2 a}{2 a + b} = \frac{b}{a + b}$ D、 $\frac{1}{- a + b} = - \frac{1}{a - b}$

查看试题解析
4. 反比例函数y= $\frac{k}{x}$ 的图象如图所示，点A是该函数图象上一点，AB垂直于x轴垂足是点B，如果S_△_AOB=1，则k的值为（）

A、1 B、﹣1 C、2 D、﹣2

查看试题解析
5. 绿化队原来用浸灌方式浇绿地，x天用水m吨，现在改用喷灌方式，可使这些水多用4天，那么现在比原来每天节约用水的吨数为（）

A、 $\frac{4 x}{m}$ B、 $\frac{x m}{x + 4}$ C、 $\frac{4 m}{x}$ D、 $\frac{4 m}{x (x + 4)}$

查看试题解析
6. 用换元法解方程： $\frac{x^{2} - 2}{x} + \frac{2 x}{x^{2} - 2}$ ＝3时，若设 $\frac{x^{2} - 2}{x} = y$ ，并将原方程化为关于y的整式方程，那么这个整式方程是（）

A、y²﹣3y+2＝0 B、y²﹣3y﹣2＝0 C、y²+3y+2＝0 D、y²+3y﹣2＝0

查看试题解析
7. 关于反比例函数y= $\frac{2}{x}$ 的图象，下列说法正确的是（）

A、图象经过点（1，1） B、两个分支分布在第二、四象限 C、两个分支关于x轴成轴对称 D、当x＜0时，y随x的增大而减小

查看试题解析
8. 如图，若反比例函数 $y = \frac{k}{x}$ 的图象与直线y＝3x+m相交于点A，B，结合图象求不等式 $3 x + m ≻ \frac{k}{x}$ 的解集（）

A、0＜x＜1 B、﹣1＜x＜0 C、x＜﹣1或0＜x＜1 D、﹣1＜x＜0或x＞1

查看试题解析

二、填空题

9. 若式子 $\frac{x^{2} - 1}{(x - 1) (x + 2)}$ 的值为零，则x的值为．

查看试题解析
10. 若 $\frac{m}{n} = 2$ ，则 $\frac{m + 3 n}{m - n}$ =.

查看试题解析
11. 已知y与x成反比例，且当x＝－3时，y＝4，则当x＝6时，y的值为.

查看试题解析
12. 若把分式 $\frac{x + 3 y}{2 x}$ 的x、y同时扩大10倍，则分式的值（填变大，变小，不变）

查看试题解析
13. 在平面直角坐标系中，已知反比例函数 $y = \frac{6}{x}$ 的图象经过P₁(2，y₁)、P₂(3，y₂)两点，若则y₁y₂.(填“＞”“＜”“＝”)

查看试题解析
14. 关于 $x$ 的分式方程 $\frac{1 - a}{x - 2} = \frac{a}{2}$ 的解是正数，则 $a$ 的取值范围是.

查看试题解析
15. 如图，点P为函数y＝ $\frac{2}{x}$ （x＞0）图象上一点，过点P作x轴、y轴的平行线，分别与函数y＝ $\frac{10}{x}$ （x＞0）的图象交于点A、B，则△AOB的面积为.

查看试题解析
16. 已知关于x的方程 $\frac{2x + m}{x - 2} = 3$ 的解是非负数，求m的取值范围.

查看试题解析

三、解答题

17. 验光师测的一组关于近视眼镜的度数y与镜片的焦距x的数据，如表：
y（单位：度）
100
200
400
500
…
x（单位：米）
1.00
0.50
0.25
0.20
…
则y关于x的函数关系式是　　．

查看试题解析
18. 化简：

(1)、 $\frac{a^{2}}{a - 1} - \frac{2 a}{1 - a}$

(2)、 $\frac{x}{x^{2} - 1} \div (1 - \frac{1}{x + 1})$

查看试题解析
19. 解方程： $\frac{1}{x - 2} + 3 = \frac{1 - x}{2 - x}$ .

查看试题解析
20. 已知： $\frac{1}{a} - \frac{1}{b} = 2$ ，则 $\frac{a - 2 a b - b}{2 a - 2 b + 7 a b}$ 的值等于多少？

查看试题解析
21. 已知反比例函数 $y = \frac{k - 1}{x}$ ，（k为常数，k≠1）．

(1)、若点A（1，2）在这个函数的图象上，求k的值；

(2)、若在这个函数图象的每一分支上，y随x的增大而增大，求k的取值范围；

(3)、若k=13，试判断点B（3，4），C（2，5）是否在这个函数的图象上，并说明理由．

查看试题解析
22. 某公司购买了一批A、B型芯片，其中A型芯片的单价比B型芯片的单价少9元，已知该公司用3120元购买A型芯片的条数与用4200元购买B型芯片的条数相等.

(1)、求该公司购买的A、B型花片的单价各是多少元？

(2)、若两种芯片共购买了200条，且购买的总费用不超过6300元，求A型芯片至少购买多少条？

查看试题解析
23. 如图，一次函数y=kx+b与反比例函数y= $\frac{m}{x}$ 的图象交于A（n ， 3），B（-3，-2）两点．

(1)、求反比例函数与一次函数的解析式；

(2)、过点B作BC⊥x轴，垂足为C ，求S_△_ABC ．

查看试题解析
24.
某气球内充满了一定量的气体，当温度不变时，气球内气体的气压p（kPa）是气体体积V（m³）的反比例函数，其图象如图所示．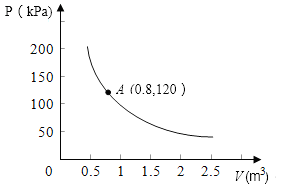

(1)、求这一函数的解析式；

(2)、当气体体积为1m³时，气压是多少？

(3)、当气球内的气压大于140kPa时，气球将爆炸，为了安全起见，气体的体积应不小于多少？（精确到0.01m³）．

查看试题解析
25. 自学下面材料后，解答问题
分母中含有未知数的不等式叫做分式不等式，如： $\frac{x - 2}{x + 1} > 0$ ； $\frac{2 x - 3}{x - 1} < 0$ 等 $.$ 那么如何求出它们的解集呢？

(1)、根据我们学过的有理数除法法则可知：两数相除，同号得正，异号得负 $.$ 其字母表达式为：
①若 $a > 0$ ， $b > 0$ ，则 $\frac{a}{b} > 0$ ；若 $a < 0$ ， $b < 0$ ，则 $\frac{a}{b} > 0$

②若 $a > 0$ ， $b < 0$ ，则 $\frac{a}{b} < 0$ ；若 $a < 0$ ， $b > 0$ ，则 $\frac{a}{b} < 0$

反之：①若 $\frac{a}{b} > 0$ ，则 ${\begin{matrix} a > 0 \\ b > 0 \end{matrix}$ 或 ${\begin{matrix} a < 0 \\ b < 0 \end{matrix}$

②若 $\frac{a}{b} < 0$ ，则或.

查看试题解析
26. 如图，矩形ABCD的两边AD，AB的长分别为3，8，且B，C在x轴的负半轴上，E是DC的中点，反比例函数y＝ $\frac{m}{x}$ （x＜0）的图象经过点E，与AB交于点F.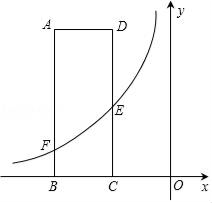

(1)、若点B坐标为（﹣6，0），求m的值；

(2)、若AF﹣AE＝2.且点E的横坐标为a.则点F的横坐标为（用含a的代数式表示），点F的纵坐标为，反比例函数的表达式为.

查看试题解析
27. 观察下列等式：
$\frac{1}{1 \times 2}$ ＝1﹣ $\frac{1}{2}$ ， $\frac{1}{2 \times 3} = \frac{1}{2} - \frac{1}{3}$ ； $\frac{1}{3 \times 4} = \frac{1}{3} - \frac{1}{4}$ ，……，

将以上二个等式两边分别相加得：

$\frac{1}{1 \times 2}$ ++ $\frac{1}{2 \times 3}$ + $\frac{1}{3 \times 4}$ ＝1﹣ $\frac{1}{2}$ + $\frac{1}{2}$ ﹣ $\frac{1}{3}$ + $\frac{1}{3}$ ﹣ $\frac{1}{4}$ ＝ $\frac{3}{4}$

用你发现的规律解答下列问题：

(1)、直接写出下列各式的计算结果：
① $\frac{1}{1 \times 2}$ + $\frac{1}{2 \times 3}$ + $\frac{1}{3 \times 4}$ +…+ $\frac{1}{2012 \times 2011}$ ＝；

② $\frac{1}{1 \times 2}$ + $\frac{1}{2 \times 3}$ + $\frac{1}{3 \times 4}$ +…+ $\frac{1}{n (n + 1)}$ ＝；

(2)、仿照题中的计算形式，猜想并写出： $\frac{1}{n (n + 3)}$ ＝；

(3)、解方程： $\frac{1}{x (x + 3)}$ + $\frac{1}{(x + 3) (x + 6)}$ + $\frac{1}{(x + 6) (x + 9)}$ ＝ $\frac{3}{2 x + 18}$ .

查看试题解析

y（单位：度）	100	200	400	500	…
x（单位：米）	1.00	0.50	0.25	0.20	…