湖北省武汉市蔡甸区八校联盟2018-2019学年八年级下学期数学5月月考试卷

试卷更新日期：2019-07-08 类型：月考试卷

进入出卷网下载

一、单选题

1. 在函数 $y = \sqrt{x - 3}$ 中，自变量 $x$ 的取值范围是（）

A、 $x < 3$ B、 $x > 3$ C、 $x \geq 3$ D、 $| \overset{⇀}{O A} | = 8 ， | \overset{⇀}{O B} | = 5$

查看试题解析
2. 下列计算正确的是（）

A、3 $\sqrt{3}$ － $\sqrt{3}$ =3 B、2+ $\sqrt{3}$ =2 $\sqrt{3}$ C、 $\sqrt{{(- 2)}^{2}}$ =－2 D、 $\sqrt{8}$ =2 $\sqrt{2}$

查看试题解析
3. 下列各式是最简二次根式的是（）

A、 $\sqrt{x^{2} + 1}$ B、 $\sqrt{\frac{4}{5}}$ C、 $\sqrt{a^{2} b^{5}}$ D、 $\sqrt{24}$

查看试题解析
4. a、b、c为△ABC三边，满足下列条件的三角形不是直角三角形的是（）

A、∠C=∠A-∠B B、a:b:c = 1 : $\sqrt{3}$ : $2$ C、∠A∶∠B∶∠C＝5∶4∶3 D、 $a = \frac{3}{5} c$ ， $b = \frac{4}{5} c$

查看试题解析
5. 如图，正方形网格中，每个正方形的边长为1，则网格上的⊿ABC中，边长为无理数的边数是（）

A、0 B、1 C、2 D、3

查看试题解析
6. 菱形的周长为16，高为2 $\sqrt{3}$ ，则菱形两邻角的度数比为（）

A、2：1 B、3：1 C、4：1 D、5：1

查看试题解析
7. 如图分别给出了变量x与y之间的对应关系，其中y不是x的函数是（）

A、 B、 C、 D、

查看试题解析
8. 将10个边长为1的正方形如图摆放在平面直角坐标系中，经过原点的一条直线将这10个正方形分成面积相等的两部分，则该直线的解析式为（）

A、y=x B、y= $\frac{9}{14}$ x C、y= $\frac{2}{3}$ x D、y= $\frac{3}{5}$ x

查看试题解析
9. 如图所示图象（折线ABCDE）描述了轮船在海上沿笔直路线行驶过程中，轮船离出发地的距离s（千米）和行驶时间t（小时）之间的函数关系，根据图中提供的信息，给出下列说法：①轮船共行驶了120千米；②轮船在行驶途中停留了0.5小时；③轮船在整个过程中的平均速度为 $\frac{160}{3}$ 千米/时；④轮船自出发后3小时至4.5小时之间行驶的速度在逐渐减少，其中正确的说法共有（）

A、1个 B、2个 C、3个 D、4 个

查看试题解析
10. 如图，平行四边形ABCD中，E是BC边上的一点，且AB=AE，若AE平分∠DAB，∠EAC=20°，则∠AED的度数为（）

A、70° B、75° C、80° D、85°

查看试题解析

二、填空题

11. 计算： $\sqrt{18} =$ ； $\sqrt{\frac{2}{3}}$ =； ${(2 \sqrt{3})}^{2}$ =；

查看试题解析
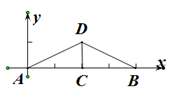
12. 已知 $a = \sqrt{2} - 1$ ，则 $a^{2} + 2a + 1$ 的值是.

查看试题解析
13. 如图，长为8 cm的橡皮筋放置在x轴上，固定两端A和B，然后把中点C向上拉升3 cm到点D，则橡皮筋被拉长了 cm.

查看试题解析
14. 如图，在矩形ABCD中，E为边AB的中点，将△CBE沿CE翻折得到△CFE，连接AF，若∠EAF=70°，那么∠BCF=度.

查看试题解析
15. 已知正比例函数y= (2-3k)x图像上有两点A（x₁,y₁）,B(x₂,y₂),当x₁>x₂时,y₁<y₂,则k的取值范围是

查看试题解析
16. 在Rt△ABC中，∠C=90°，AB=5，BC=3，点D、E分别在BC、AC上，且BD=CE，设点C关于DE的对称点为F，若DF∥AB，则BD的长为.

查看试题解析

三、解答题

17. 计算：

(1)、 $\sqrt{2} (\sqrt{2} - \sqrt{3}) + \sqrt{6}$

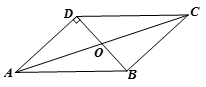
(2)、（ $\sqrt{48}$ －3 $\sqrt{27}$ ）÷ $\sqrt{6}$

查看试题解析
18. 若x、y为实数，且 $y > \sqrt{x - 2} + \sqrt{2 - x} + 2$ ，化简： $\frac{1}{2 - y} \sqrt{y^{2} - 4 y + 4} + \sqrt{2 x}$

查看试题解析
19. 在四边形ABCD中，对角线AC、BD交于点O，若AD=12，OD=OB=5，AC=26，∠ADB=90º，求证：四边形ABCD为平行四边形.

查看试题解析
20. 如图，正方形网格中的每个小正方形边长都是1.

(1)、如图1，在4×4的方格中，画一个三角形，使它的三边长分别是3， $\frac{x_{1}}{x_{2}}$ ， $\sqrt{5}$ ，且顶点都在格点上；

(2)、如图2 ，直接写出：①△ABC的周长为 ②△ABC的面积为；③AB边上的高为.

查看试题解析
21. 如图，在Rt△ACB中，∠ACB=90º，点D是AB的中点，点E是CD的中点，过C作CF∥AB交AE的延长线于点F，连BF.

(1)、求证：△ADE≌△FCE；

(2)、若∠DCF=120º，DE=2，求BC的长.

查看试题解析
22. 已知正比例函数y=kx经过点A，点A在第四象限，过点A作AH⊥x轴，垂足为点H，点A的横坐标为3，且△AOH的面积为3.

(1)、求正比例函数的解析式；

(2)、在x轴上能否找到一点P，使△AOP的面积为5？若存在，求点P的坐标；若不存在，请说明理由.

查看试题解析
23. 在菱形ABCD中，∠BAD＝60°

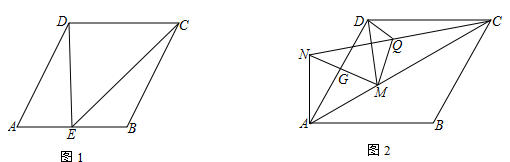(1)、如图1，点E为线段AB的中点，连接DE、CE.若AB＝4，求线段EC的长

(2)、如图2，M为线段AC上一点（不与A、C重合），以AM为边向上构造等边三角形AMN，线段MN与AD交于点G，连接NC、DM，Q为线段NC的中点，连接DQ、MQ，判断DM与DQ的数量关系，并证明你的结论

(3)、在(2)的条件下，若AC＝ $\sqrt{3}$ ，请你直接写出DM＋CN的最小值

查看试题解析
24. 如图1，在平面直角坐标系中，已知A（a，b），且a、b满足 $b = \sqrt{a - 2} + \sqrt{2 - a} + 1$ ，

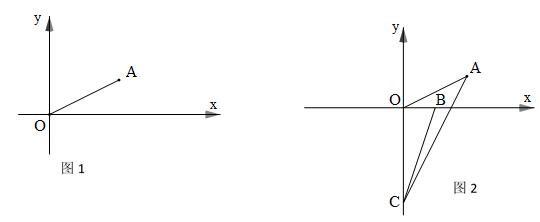(1)、求A点的坐标及线段OA的长度；

(2)、点P为x轴正半轴上一点，且△AOP是等腰三角形，求P点的坐标；

(3)、如图2，若B（1，0），C（0，－3），试确定∠ACO+∠BCO的值是否发生变化，若不变，求其值；若变化，请求出变化范围

查看试题解析