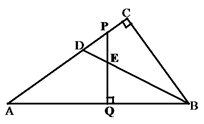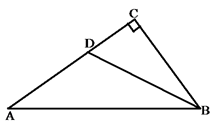江苏省苏南五市联考2018-2019学年七年级下学期数学期中考试试卷
试卷更新日期:2019-07-08 类型:期中考试
一、单选题
-
1. 如图,A,B,C,D中的哪幅图案可以通过图案①平移得到( )
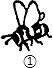 A、
A、 B、
B、 C、
C、 D、
D、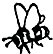 2. 每到四月,许多地方杨絮、柳絮如雪花般漫天飞舞,人们不堪其忧。据测定,杨絮纤维的直径约 ,该数值用科学记数法表示为( )A、 B、 C、 D、3. 以下列各组数据为边长,能构成三角形的是( )A、3,4,5 B、4,4,8 C、3,10,4 D、4,5,104. 一个多边形的每个内角都等于140°,则这个多边形的边数是( )A、7 B、8 C、9 D、105. 下列等式正确的是( )A、 B、 C、 D、6. 已知x2-2mx+25是完全平方式,则m的值为( )A、5 B、±5 C、10 D、±107. 若a=-0.32 , b=-3-2 , c=(- )-2 , d=(- )0 , 则它们的大小关系是( )A、a<c<b<d B、b<a<d<c C、a<b<d<c D、b<a<c<d8. 如图,有一条直的宽纸带,按图折叠,则∠α的度数等于( )
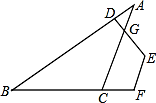
2. 每到四月,许多地方杨絮、柳絮如雪花般漫天飞舞,人们不堪其忧。据测定,杨絮纤维的直径约 ,该数值用科学记数法表示为( )A、 B、 C、 D、3. 以下列各组数据为边长,能构成三角形的是( )A、3,4,5 B、4,4,8 C、3,10,4 D、4,5,104. 一个多边形的每个内角都等于140°,则这个多边形的边数是( )A、7 B、8 C、9 D、105. 下列等式正确的是( )A、 B、 C、 D、6. 已知x2-2mx+25是完全平方式,则m的值为( )A、5 B、±5 C、10 D、±107. 若a=-0.32 , b=-3-2 , c=(- )-2 , d=(- )0 , 则它们的大小关系是( )A、a<c<b<d B、b<a<d<c C、a<b<d<c D、b<a<c<d8. 如图,有一条直的宽纸带,按图折叠,则∠α的度数等于( )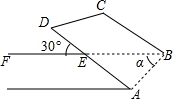 A、50° B、60° C、75° D、85°9. 将 沿 翻折,顶点 均落在点 处,且 与 重合于线段 ,若 ,则 的度数( )A、40° B、37° C、36° D、32°10. 现有 张卡片,在卡片上分别写上-2、0、1中的任意一个数,记为 ,若将卡片上的数求和,得 ;若将卡片上的数先平方再求和,得 ,则写数字“1”的卡片的张数为( )A、35 B、28 C、33 D、20
A、50° B、60° C、75° D、85°9. 将 沿 翻折,顶点 均落在点 处,且 与 重合于线段 ,若 ,则 的度数( )A、40° B、37° C、36° D、32°10. 现有 张卡片,在卡片上分别写上-2、0、1中的任意一个数,记为 ,若将卡片上的数求和,得 ;若将卡片上的数先平方再求和,得 ,则写数字“1”的卡片的张数为( )A、35 B、28 C、33 D、20二、填空题
-
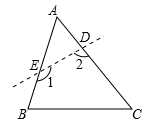
11. 等腰三角形的两边长分别是3cm和6cm,则它的周长是cm.12. 如果 的乘积中不含 项,则m为.13. 如图,在△ABC中,∠A=60°,若剪去∠A得到四边形BCDE,则∠1+∠2=.
 14. 已知9x=4,3y=2,则(1) =;(2) =.15.
14. 已知9x=4,3y=2,则(1) =;(2) =.15.将一副学生用三角板按如图所示的方式放置.若AE∥BC,则∠AFD的度数是
 16. 若 =1,则x的值为.17. 如图,△ABC的面积为40cm2 , AE=ED,BD=3DC,则图中△AEF的面积等于cm2.
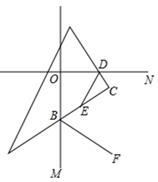
16. 若 =1,则x的值为.17. 如图,△ABC的面积为40cm2 , AE=ED,BD=3DC,则图中△AEF的面积等于cm2.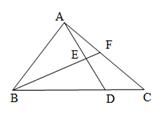 18. 如图,在△AOB和△COD中,∠AOB=∠COD=90°,∠B=50°,∠C=60°,点D在边OA上,将图中的△COD绕点O按每秒20°的速度沿顺时针方向旋转一周,在旋转的过程中,在第t秒时,边CD恰好与边AB平行,则t的值为.
18. 如图,在△AOB和△COD中,∠AOB=∠COD=90°,∠B=50°,∠C=60°,点D在边OA上,将图中的△COD绕点O按每秒20°的速度沿顺时针方向旋转一周,在旋转的过程中,在第t秒时,边CD恰好与边AB平行,则t的值为.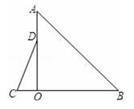
三、解答题
-
19. 计算:(1)、(2)、(3)、(4)、20. 若x+y=3,且(x-3)(y-3)=6.(1)、求xy的值;(2)、求 的值.21. 先化简,再求值: ,其中a=-1,b=2.22. 如图:在正方形网格中有一个△ABC,按要求进行下列作图(只能借助于网格):
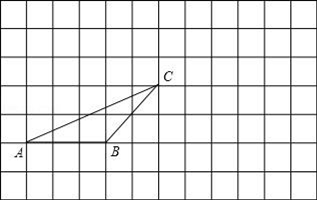 (1)、①画出△ABC中BC边上的高AD;
(1)、①画出△ABC中BC边上的高AD;②画出先将△ABC向右平移6格,再向上平移3格后的△A1B1C1;
(2)、画一个△BCP(要求各顶点在格点上,P不与A点重合),使其面积等于△ABC的面积.并回答,满足这样条件的点P共个.23. 如图,DE⊥AB,EF∥AC,∠A=24°,求∠DEF的度数.