云南省楚雄州2017-2018学年七年级下学期数学期末考试试卷
试卷更新日期:2019-07-08 类型:期末考试
一、单选题
-
1. 下面有4个汽车标志图案,其中是轴对称图形的有( )
 A、1个 B、2个 C、3个 D、4个2. 如图是小明用八个相同的小正方体搭建的一个积木,它的左视图是( )
A、1个 B、2个 C、3个 D、4个2. 如图是小明用八个相同的小正方体搭建的一个积木,它的左视图是( ) A、
A、 B、
B、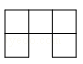 C、
C、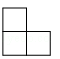 D、
D、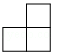 3. 下列说法中,正确的是( )A、随机事件发生的概率为 B、概率很小的事件不可能发生 C、投掷一枚质地均匀的硬币100次,正面朝上的次数一定为50次 D、不可能事件发生的概率为04. 下列各组线段能组成三角形的是 ( )A、3cm、3cm、6cm B、7cm、4cm、5cm C、3cm、4cm、8cm D、4.2cm、2.8cm、7cm5. 下列运算正确的是( )A、 B、 C、 D、6. 有理数 , 在数轴上的对应点的位置如图所示,则正确的结论是( )
3. 下列说法中,正确的是( )A、随机事件发生的概率为 B、概率很小的事件不可能发生 C、投掷一枚质地均匀的硬币100次,正面朝上的次数一定为50次 D、不可能事件发生的概率为04. 下列各组线段能组成三角形的是 ( )A、3cm、3cm、6cm B、7cm、4cm、5cm C、3cm、4cm、8cm D、4.2cm、2.8cm、7cm5. 下列运算正确的是( )A、 B、 C、 D、6. 有理数 , 在数轴上的对应点的位置如图所示,则正确的结论是( ) A、 B、 C、 D、7. 如图,直线 ∥ ,直线 与直线 、 分别交于点A,点B,AC⊥AB于点A,交直线 于点C.如果∠1 = 34°,那么∠2的度数为( )
A、 B、 C、 D、7. 如图,直线 ∥ ,直线 与直线 、 分别交于点A,点B,AC⊥AB于点A,交直线 于点C.如果∠1 = 34°,那么∠2的度数为( )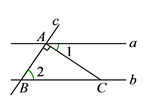 A、34° B、56° C、66° D、146°8. 已知线段AB,延长AB到点C,使BC= AB,D为AC的中点,若AB=9 cm,则DC的长为( )A、3 cm B、6 cm C、1 cm D、12 cm
A、34° B、56° C、66° D、146°8. 已知线段AB,延长AB到点C,使BC= AB,D为AC的中点,若AB=9 cm,则DC的长为( )A、3 cm B、6 cm C、1 cm D、12 cm二、填空题
-
9. 的倒数是10. 根据央视报道,去年我国汽车尾气排放总量大约为47000000吨.将47000000用科学记数法表示为.11. 如图,已知AD=AE,请你添加一个条件使△ABE ≌ △ACD,你添加的条件是(填一个即可).
 12. 已知一个水池有水50吨,现将水排出,如果排水管每小时的流量是10吨,水池中的余水量Q(吨)与排水时间t(小时)的关系式为:.13. 如图,在△ABC中,AB=10cm,AC=8cm,BC的垂直平分线分别交 AB、BC于D、E,则△ACD的周长为cm.
12. 已知一个水池有水50吨,现将水排出,如果排水管每小时的流量是10吨,水池中的余水量Q(吨)与排水时间t(小时)的关系式为:.13. 如图,在△ABC中,AB=10cm,AC=8cm,BC的垂直平分线分别交 AB、BC于D、E,则△ACD的周长为cm. 14.
14.下列图形:它们是按一定规律排列的,依照此规律,第n个图形共有个★.

三、解答题
-
15. 计算:(1)、(2)、16. 先化简,再求值.已知 ,求代数式 的值.17. 某中学校团委开展“关爱残疾儿童”爱心捐书活动,全校师生踊跃捐赠各类书籍共6000本.为了解各类书籍的分布情况,从中随机抽取了部分书籍分四类进行统计:A.艺术类;B.文学类;C.科普类;D.其他,并将统计结果绘制成如图所示的两幅不完整的统计图.
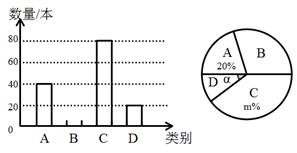 (1)、这次统计共抽取了本书籍,扇形 统计图中的m= , ∠α的度数是;(2)、请将条形统计图补充完整;(3)、估计全校师生共捐赠了多少本文学类书籍.18. 某商场举行开业酬宾活动,设立了两个可以自由转动的转盘(如图所示,两个转盘均被等分),并规定:顾客购买满188元的商品,即可任选一个转盘转动一次,转盘停止后,指针所指区域内容即为优惠方式;若指针所指区域空白,则无优惠.已知小张在该商场消费300元
(1)、这次统计共抽取了本书籍,扇形 统计图中的m= , ∠α的度数是;(2)、请将条形统计图补充完整;(3)、估计全校师生共捐赠了多少本文学类书籍.18. 某商场举行开业酬宾活动,设立了两个可以自由转动的转盘(如图所示,两个转盘均被等分),并规定:顾客购买满188元的商品,即可任选一个转盘转动一次,转盘停止后,指针所指区域内容即为优惠方式;若指针所指区域空白,则无优惠.已知小张在该商场消费300元 (1)、若他选择转动转盘1,则他能得到优惠的概率为多少?(2)、选择转动转盘1和转盘2,哪种方式对于小张更合算,请通过计算加以说明.19. 下列为边长为1的小正方形组成的网格图.(1)、请画出△ABC关于直线
(1)、若他选择转动转盘1,则他能得到优惠的概率为多少?(2)、选择转动转盘1和转盘2,哪种方式对于小张更合算,请通过计算加以说明.19. 下列为边长为1的小正方形组成的网格图.(1)、请画出△ABC关于直线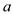 对称的图形△A1B1C1(不要求写作法);
对称的图形△A1B1C1(不要求写作法);  (2)、△ABC的面积为(直接写出即可);(3)、如图,P为直线 上一点,若点P到AC的距离为 ,则点P到AC1的距离是.20. 如图是甲、乙两人从同一地点出发后,路程随时间变化的图象.
(2)、△ABC的面积为(直接写出即可);(3)、如图,P为直线 上一点,若点P到AC的距离为 ,则点P到AC1的距离是.20. 如图是甲、乙两人从同一地点出发后,路程随时间变化的图象.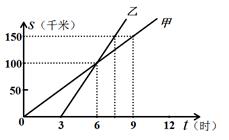 (1)、此变化过程中, 是自变量, 是因变量.(2)、甲的速度 乙的速度.(填“大于”、“等于”、或“小于”)(3)、甲与乙 时相遇.(4)、甲比乙先走 小时.(5)、9时甲在乙的 (填“前面”、“后面”、“相同位置”).(6)、路程为150km,甲行驶了 小时,乙行驶了 小时.21. 如图,完成下列推理过程:
(1)、此变化过程中, 是自变量, 是因变量.(2)、甲的速度 乙的速度.(填“大于”、“等于”、或“小于”)(3)、甲与乙 时相遇.(4)、甲比乙先走 小时.(5)、9时甲在乙的 (填“前面”、“后面”、“相同位置”).(6)、路程为150km,甲行驶了 小时,乙行驶了 小时.21. 如图,完成下列推理过程:如图所示,点E在△ABC外部,点D在BC边上,DE交AC于F,若∠1=∠3,∠E=∠C,AE=AC,求证:△ABC≌△ADE.
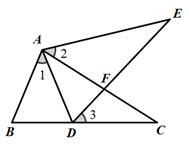
证明:∵ ∠E=∠C(已知),
∠AFE=∠DFC(),
∴∠2=∠3(),
又∵∠1=∠3(),
∴ ∠1=∠2(等量代换),
∴+∠DAC= +∠DAC(),
即∠BAC =∠DAE,
在△ABC和△ADE中
∵
∴△ABC≌△ADE().
22. 某班计划买一些乒乓球和乒乓球拍,现了解情况如下:甲、乙两家商店出售两种同样品牌的乒乓球和乒乓球拍,乒乓球拍每副定价100元,乒乓球每盒定价25元.经洽谈后,甲店每买一副球拍赠一盒乒乓球,乙店全部按定价的9折优惠.该班需球拍5副,乒乓球若干盒(不少于5盒).问:(1)、当分别购买20盒、40盒乒乓球时,去哪家商店购买更合算?(2)、当购买乒乓球多少盒时,两种优惠办法付款一样?23. 如图1,点A、B在直线 上,点C、D在直线 上,AE平分∠BAC,CE平分∠ACD,∠EAC+∠ACE=90° .
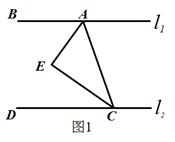
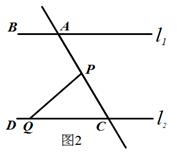
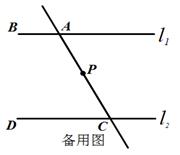 (1)、请判断 与 的位置关系并说明理由;(2)、如图2,在(1)的结论下,P为线段AC上一定点,点Q为直线CD上一动点,当点Q在射线CD上运动时(不与点C重合)∠CPQ+∠CQP与∠BAC有何数量关系?请说明理由.
(1)、请判断 与 的位置关系并说明理由;(2)、如图2,在(1)的结论下,P为线段AC上一定点,点Q为直线CD上一动点,当点Q在射线CD上运动时(不与点C重合)∠CPQ+∠CQP与∠BAC有何数量关系?请说明理由.