云南省保山市腾冲县2017-2018学年七年级下学期数学期末考试试卷
试卷更新日期：2019-07-08 类型：期末考试
一、单选题
-
1. 计算± 的值为（ ）A、±3 B、±9 C、3 D、92. 2013月5日，李克强总理在总结过去五年的政府工作时指出，中央财政加大对各类学校家庭困难学生资助力度，4.3亿人次受益，4.3亿用科学记数法表示为（ ）A、 4.3×106 B、4.3×107 C、4.3×108 D、4.3×1093. 在平面直角坐标系中，点P(2，－3)在（ ）A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 如图，DE经过点A，DE∥BC，下列说法错误的是（ ）
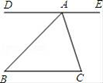A、∠DAB＝∠EAC B、∠EAC＝∠C C、∠EAB+∠B＝180° D、∠DAB＝∠B5. 如图，轮船与灯塔相距120nmile，则下列说法中正确的是（ ）
A、轮船在灯塔的北偏西65°，120 n mile处 B、灯塔在轮船的北偏东25°，120 n mile处 C、轮船在灯塔的南偏东25°，120 n mile处 D、灯塔在轮船的南偏西65°，120 n mile处6. 若a＞b，则下列各式中不正确的是（ ）A、7+a＞7+b B、a﹣7＞b﹣7 C、7a＞7b D、﹣ ＞﹣7. 下列调查方式中适合的是（ ）A、要了解一批节能灯的使用寿命，采用普查方式 B、调查你所在班级同学的身高，采用抽样调查方式 C、环保部门调查长江某段水域的水质情况，采用抽样调查方式 D、调查全市中学生每天的就寝时间，采用普查方式8. 如图，观察下列图形，第一个图形有3个三角形，第二个图形有7个三角形，第三个图形有11个三角形，依照此规律，第12个图形中共有（ ）个三角形.
A、47 B、43 C、39 D、36二、填空题
-
9. 计算：｜一 ｜＝.10. 计算： ＝.11. 由 ﹣3y＝6可以得到用x表示y的式子是.12. 若a、b满足|a﹣2|+（3﹣b）2＝0，则 ＝.13. 某商店以每件180元的进价购入T恤衫60件，并以每件240元的价格销售.一个月后T恤衫的销售款已经超过这批T恤衫的进货款，这时至少已售出T恤衫件.14. 如图，△ABC的顶点都在网格点上，将△ABC向右平移3个单位长度，再向上平移2个单位长度，则平移后得到的△A′B′C′三个顶点A′、B′、C′的坐标分别是.
三、解答题
-
15. 计算：（﹣5）3÷（﹣ ）﹣16. 先化简，再求值：5x3﹣[6x2﹣（3x2+4）﹣4x3]，其中x＝﹣3.17. 解不等式组 ，并把它的解集在数轴上表示出来.18. 解方程组19. 甲、乙两个工人同时接受一批任务，上午工作的5小时中，甲用了2小时改装机器以提高工效，因此，上午工作结束时，甲比乙少做60个零件；下午两人继续工作4小时后，全天总计甲反而比乙多做468个零件，问这一天甲、乙每小时各做多少个零件？20. 如图，∠AOB内有一点P；
①过点P画PE⊥OB，PF⊥OA，垂足分别为E，F.
②过点P画PM∥OB，交OA于点M；
③画射线OP；
④分别写出图中相等的角、互补的角、互余的角各一对.
21. 如图，已知：AB∥DE，∠1+∠3＝180°，求证：BC∥EF.
22. 勤俭节约一直是中华民族的传统美德，某中学校团委准备以“勤俭节约”为主题开展一次演讲比赛，为此先对同学们每月零花钱的数额进行一些了解，随机调查了本校部分同学，根据调查结果，绘制出了如下两个尚不完整的统计图表.组别
分组（单位：元）
人数
A
0≤x＜30
4
B
30≤x＜60
a
C
60≤x＜90
b
D
90≤x＜120
8
E
120≤x＜150
2
根据以上图表，解答下列问题：
(1)、填空：这次调查的同学共有人，a+b＝ ， m＝；(2)、求扇形统计图中扇形B的圆心角的度数；(3)、该校共有1200名学生，请估计每月零花钱的数额在60≤x＜90范围的人数.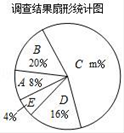
23. 已知∠AOB是一个直角，作射线OC，再分别作∠AOC和∠BOC的平分线OD，OE.
(1)、如图①，当∠BOC＝40°时，求∠DOE的度数；(2)、如图②，当射线OC在∠AOB内绕O点旋转时，∠DOE的大小是否发生变化，说明理由；(3)、当射线OC在∠AOB外绕O点旋转且∠AOC为钝角时，画出图形，直接写出∠DOE的度数（不必写过程）.