广西玉林市玉州区2017-2018学年七年级下学期数学期末考试试卷

试卷更新日期：2019-07-08 类型：期末考试

进入出卷网下载

一、单选题

1. 下面四个图形中，∠1与∠2是对顶角的是（）

A、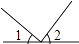 B、 C、 D、

查看试题解析
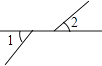2. 用统计图来描述某班同学的身高情况，最合适的是 $($ $)$

A、频数分布直方图 B、条形统计图 C、扇形统计图 D、折线统计图

查看试题解析
3. 如果a＞b，那么下列结论一定正确的是（）

A、a-3＜b-3 B、3-a＜3-b C、ac²＞bc² D、a²＞b²

查看试题解析
4. 下列方程是二元一次方程的是（）

A、2x+y=z-3 B、xy=5 C、 $\frac{1}{x} + 5 = 3 y$ D、x=y

查看试题解析
5. 如图，下列判断中正确的是（）

A、如果∠3+∠2=180°，那么AB∥CD B、如果∠1+∠3=180°，那么AB∥CD C、如果∠2=∠4，那么AB∥CD D、如果∠1=∠5，那么AB∥CD

查看试题解析
6. 在下列四项调查中，方式正确的是 $($ $)$

A、了解本市中学生每天学习所用的时间，采用全面调查的方式 B、为保证运载火箭的成功发射，对其所有的零部件采用抽样调查的方式 C、了解某市每天的流动人口数，采用全面调查的方式 D、了解全市中学生的视力情况，采用抽样调查的方式

查看试题解析
7.
一个不等式组中的两个不等式的解集如图所示，则这个不等式组的解集为（）

A、x＞﹣1 B、x＜1 C、﹣1≤x＜1 D、﹣1＜x≤1

查看试题解析
8. 如图，在一个三角形三个顶点和中心处的每个“ $○$ ”中各填有一个式子，如果图中任意三个“ $○$ ”中的式子之和均相等，那么a的值为 $($ $)$

A、1 B、2 C、3 D、0

查看试题解析
9. 不等式组 ${\begin{matrix} 5 x - 3 < 3 x + 5 \\ x < a \end{matrix}$ 的解集为x＜4，则a满足的条件是（）

A、a＜4 B、a=4 C、a≤4 D、a≥4

查看试题解析
10. 如图，AF∥CD，BC平分∠ACD，BD平分∠EBF，且BC⊥BD.下列结论：①BC平分∠ABE；②AC∥BE；③∠BCD+∠D=90°；④∠DBF=2∠ABC．其中正确的个数为（）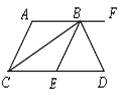

A、1个 B、2个 C、3个 D、4个

查看试题解析
11. 若关于x的不等式组 ${\begin{matrix} x - a > 0 \\ \frac{3 x - 1}{5} < 1 \end{matrix}$ 无解，则a的取值范围是 $($ $)$

A、 $a > 2$ B、 $a \geq 2$ C、 $1 < a \leq 2$ D、 $1 \leq a < 2$

查看试题解析
12. 如图所示在平面直角坐标系中，半径均为1个单位长度的半圆O₁、O₂、O₃ ， ……，组成一条平滑的曲线，点P从原点O出发沿这条曲线向右运动，速度为每秒 $\frac{π}{2}$ 个单位长度，则第2019秒时，点P的坐标是（）

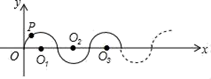A、（2018，0） B、（2019，1） C、（2019，﹣1） D、（2020，0）

查看试题解析

二、填空题

13. 已知a，b为两个连续整数，且 $a < \sqrt{13} < b$ ，则a+b= ．

查看试题解析
14. 如图，已知AB⊥CD，垂足为点O，直线EF经过O点，若∠1=55°，则∠COE的度数为度.

查看试题解析
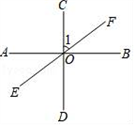15. 若关于x，y的二元一次方程组 ${\begin{matrix} 3 x + y = 1 + a \\ x + 3 y = 3 \end{matrix}$ 的解满足x+y＜2，则a的取值范围为．

查看试题解析
16. 已知直线AB∥x轴，点A的坐标为(1，2)，并且线段AB＝3，则点B的坐标为

查看试题解析
17. 定义：对于实数a，符号 $[a]$ 表示不大于a的最大整数，例如： $[4.7] = 4$ ， $[- π] = - 4$ ， $[3] = 3$ ，如果 $[\frac{x + 2}{3} + 1] = - 5$ ，则x的取值范围为.

查看试题解析
18. 已知关于x的不等式组 ${\begin{matrix} x - a \geq 0 \\ 3 - 2 x > - 1 \end{matrix}$ 的整数解共有6个，则a的取值范围是.

查看试题解析

三、解答题

19.

(1)、计算： ${(- 3)}^{2} + | 1 - \sqrt{2} | - \sqrt[3]{3^{3}}$

(2)、解方程组 ${\begin{matrix} 2 x + y = 4 \\ x + 25 = 5 \end{matrix}$

查看试题解析
20. 解不等式组： ${\begin{matrix} 4 (x + 1) \leq 7 x + 10 \\ x - 5 < \frac{x - 8}{3} \end{matrix}$ ，并写出它的所有非负整数解．

查看试题解析
21.

(1)、计算： $\sqrt{49} - \sqrt{0.64} - \sqrt[3]{125}$

(2)、已知 ${(x - 2)}^{2} = 9$ ，求x的值.

查看试题解析
22. 线段AB在直角坐标系中的位置如图.

(1)、写出A、B两点的坐标.

(2)、在y轴上找点C，使BC长度最短，写出点C的坐标.

(3)、①连接AC、BC并求出三角形ABC的面积.
②将三角形ABC平移，使点B与原点重合，画出平移后的三角形A₁B₁C₁.

查看试题解析
23. 某中学改革学生的学习模式，变“老师要学生学习”为“学生自主学习”，培养了学生自主学习的能力.小华与小明同学就“你最喜欢哪种学习方式”随机调查了他们周围的一些同学，根据收集到的数据绘制了以下两个不完整的统计图（如图）.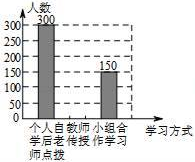

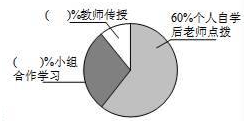
请根据上面两个不完整的统计图回答以下4个问题：

(1)、这次抽样调查中，共调查了名学生.

(2)、补全条形统计图中的缺项.

(3)、在扇形统计图中，选择教师传授的占%，选择小组合作学习的占%.

(4)、根据调查结果，估算该校1800名学生中大约有人选择小组合作学习模式.

查看试题解析
24. 为了更好改善河流的水质，治污公司决定购买10台污水处理设备.现有A，B两种型号的设备，其中每台的价格，月处理污水量如下表：经调查：购买一台A型设备比购买一台B型设备多2万元，购买2台A型设备比购买3台B型设备少6万元.

A型

B型

价格(万元/台)

a

b

处理污水量(吨/月)

240

200

(1)、求a，b的值；

(2)、治污公司经预算购买污水处理设备的资金不超过105万元，你认为该公司有哪几种购买方案；

(3)、在(2)的条件下，若每月要求处理污水量不低于2040吨，为了节约资金，请你为治污公司设计一种最省钱的购买方案.

查看试题解析
25. 如果一元一次方程的根是一元一次不等式组的解，则称该一元一次方程为该不等式组的关联方程.

(1)、在方程①3x－1=0，② $\frac{2}{3} x + 1 = 0$ ③x－(3x+1)=－5 中，不等式组 ${\begin{matrix} - x + 2 > x - 5 \\ 3 x - 1 > - x + 2 \end{matrix}$ 的关联方程是

(2)、若不等式组 ${\begin{matrix} x - \frac{1}{2} < 1 \\ 1 + x > - 3 x + 2 \end{matrix}$ 的一个关联方程的根是整数，则这个关联方程可以是（写出一个即可

(3)、若方程 3－x=2x，3+x= $2 (x + \frac{1}{2})$ 都是关于 x 的不等式组 ${\begin{matrix} x < 2 x - m \\ x - 2 \leq m \end{matrix}$ 的关联方程，直接写出 m 的取值范围.

查看试题解析
26. 如图1，在平面直角坐标系中，点A为x轴负半轴上一点，点B为x轴正半轴上一点， $C (0 ， a)$ ， $D (b ， a)$ ，其中a、b满足关系式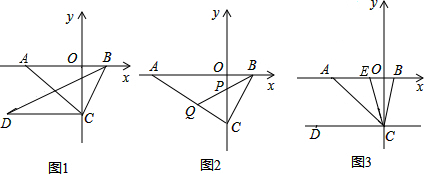： $| a + 4 | + {(b - a - 1)}^{2} = 0$ .

(1)、a= ， $b =$ ， $△ B C D$ 的面积为；

(2)、如图2，石 $A C ⊥ B C$ 于点C，点P是线段OC上一点，连接BP，延长BP交AC于点 $Q .$ 当 $∠ C P Q = ∠ C Q P$ 时，求证：BP平分 $∠ A B C$ ； $($ 提示：三角形三个内角和等于 $180^{\circ})$

(3)、如图3，若 $A C ⊥ B C$ ，点E是点A与点B之间上一点连接CE，且CB平分 $∠ E C F .$ 问 $∠ B E C$ 与 $∠ B C O$ 有什么数量关系？请写出它们之间的数量关系并请说明理由.

查看试题解析

	A型	B型
价格(万元/台)	a	b
处理污水量(吨/月)	240	200