江苏省扬州市邗江区2018-2019学年八年级下学期数学期中考试试卷

试卷更新日期：2019-07-08 类型：期中考试

进入出卷网下载

一、单选题

1. 在代数式① $\frac{1}{x}$ ；② $\frac{a + b}{5}$ ；③ $\frac{1}{2 - m}$ ；④ $\frac{1}{π - 1}$ 中，属于分式的有（）

A、①② B、①③ C、①③④ D、①②③④

查看试题解析
2. 若反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象经过点（﹣2，3），则此函数图象也经过的点是（）

A、（﹣2，-3） B、（2，3） C、（﹣1，6） D、（﹣1.5，-4）

查看试题解析
3. 下列叙述正确的是（）

A、“如果a，b是实数，那么a+b=b+a”是不确定事件 B、“某班50位同学中恰有2位同学生日是同一天”是随机事件 C、为了了解一批炮弹的杀伤力，采用普查的调查方式比较合适 D、某种彩票的中奖概率为 $\frac{1}{7}$ ，是指买7张彩票一定有一张中奖

查看试题解析
4. 下列运算正确的是（）

A、 $\frac{y}{- x - y} = \frac{y}{x - y}$ B、 $\frac{2 x + y}{3 x + y} = \frac{2}{3}$ C、 $\frac{x^{2} + y^{2}}{x + y} = x + y$ D、 $\frac{y + x}{x^{2} - y^{2}} = \frac{1}{x - y}$

查看试题解析
5. 已知 $P_{1} (x_{1}, y_{1})$ 、 $P_{2} (x_{2}, y_{2})$ 、 $P_{3} (x_{3}, y_{3})$ 是反比例函数 $y = - \frac{2019}{x}$ 的图象上的三点，且 $x_{1} < x_{2} < 0 < x_{3}$ ，则 $y_{1}$ 、 $y_{2}$ 、 $y_{3}$ 的大小关系是（）

A、 $y_{3} < y_{1} < y_{2}$ B、 $y_{1} < y_{2} < y_{3}$ C、 $y_{2} < y_{1} < y_{3}$ D、 $y_{2} < y_{3} < y_{1}$

查看试题解析
6.
如图，在四边形ABCD中，E是BC边的中点，连接DE并延长，交AB的延长线于F点，AB＝BF.添加一个条件，使四边形ABCD是平行四边形．你认为下面四个条件中可选择的是（）

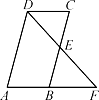A、AD＝BC B、CD＝BF C、∠A＝∠C D、∠F＝∠CDE

查看试题解析
7. 如图，小红在作线段AB的垂直平分线时，是这样操作的：分别以点A，B为圆心，大于线段AB长度一半的长为半径画弧，相交于点C，D，则直线CD即为所求。连结AC，BC，AD，BD，根据她的作图方法可知，四边形ADBC定是（）

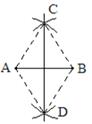A、梯形 B、矩形 C、菱形 D、正方形

查看试题解析
8. 如图，▱ABCD中，对角线AC与BD相交于点E，∠AEB=45°，BD=2，将△ABC沿AC所在直线翻折180°到其原来所在的同一平面内，若点B的落点记为B′，则DB′的长为（）

A、1 B、 $\sqrt{2}$ C、 $\frac{3}{2}$ D、 $\sqrt{3}$

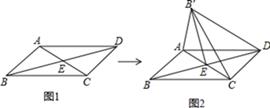查看试题解析
9. 如图，正方形ABCD的四个顶点分别在四条平行线l₁、l₂、l₃、l₄上，这四条直线中相邻两条之间的距离依次为h₁、h₂、h₃ ．若h₁=2，h₂=1，则正方形ABCD的面积为（）

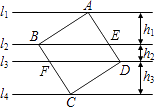A、9 B、10 C、13 D、25

查看试题解析

二、填空题

10. 已知 $\frac{a}{b} = \frac{5}{2}$ ，则 $\frac{a - b}{b} =$ .

查看试题解析
11. 当x=时，分式 $\frac{x^{2} - 9}{x - 3}$ 的值为零．

查看试题解析
12. 平行四边形ABCD中，∠A+∠C=100°，则∠B=度．

查看试题解析
13. 一组数据共有50个，分成5组后其中前四组的频数分别是3、17、15、5, 则第5组数据的频率为.

查看试题解析
14. 菱形ABCD的对角线AC，BD相交于点O，AC=10，BD=24，则菱形ABCD的周长为.

查看试题解析
15. 在四边形ABCD中，对角线AC⊥BD且AC=6、BD=8，E、F分别是边AB、CD的中点，则EF=.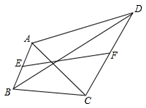

查看试题解析
16. 如图，点P是矩形ABCD的对角线AC上一点，过点P作EF∥BC，分别交AB，CD于点E，F，连接PB，PD.若AE＝2，PF＝8.则图中阴影部分的面积为.

查看试题解析
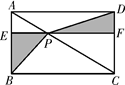17. 如图，△ABC和△BOD都是等腰直角三角形，∠ACB=∠BDO=90°，且点A在反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象上，若 $O B^{2} - A B^{2} = 8$ ，则k的值为 .

查看试题解析
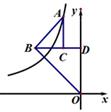18. 如图，已知直线 $l$ ∥AB， $l$ 与 AB 之间的距离为 2 ，C、D 是直线 $l$ 上l两个动点（点 C在 D 点的左侧），且 AB=CD=5.连接 AC、BC、BD，将△ABC 沿 BC 折叠得到△A′BC.若以 A′、C、B、D 为顶点的四边形为矩形，则此矩形相邻两边之和为.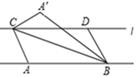

查看试题解析

三、解答题

19.

(1)、计算： $\frac{a^{2}}{a + 3} — \frac{9}{a + 3}$

(2)、解方程: $\frac{x - 8}{x - 7} + \frac{2}{7 - x} = 4$

查看试题解析
20. 化简： $(\frac{3}{x + 1} - x + 1) \div \frac{x^{2} - 2 x}{x + 1}$ ，并从﹣2＜x＜2中选一个你喜欢的整数代入求值.

查看试题解析

21. 在一个不透明的口袋里装有仅颜色不同的黑、白两种颜色的球20只，某学习小组做摸球实验.将球搅匀后从中随机摸出一个球，记下颜色，再把它放回袋中，不断重复，下表是活动进行中记下的一组数据

摸球的次数n	100	150	200	500	800	1000
摸到白球的次数m	58	96	116	295	484	601
摸到白球的频率 $\frac{m}{n}$	0.58	0.64	0.58	0.59	0.605	0.601

(1)、请你估计，当n很大时，摸到白球的频率将会接近(精确到0.1).

(2)、假如你去摸一次，你摸到白球的概率是，摸到黑球的概率是.

(3)、试估算口袋中黑、白两种颜色的球有多少只.

查看试题解析

22. 正方形网格中（网格中的每个小正方形边长是1），△ABC的顶点均在格点上，请在所给的直角坐标系中解答下列问题：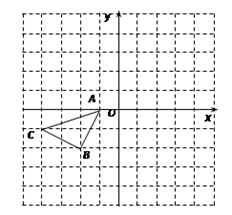

(1)、①作出△ABC绕点A逆时针旋转90°的△AB₁C₁.
②作出△ABC关于原点O成中心对称的△A₁B₂C₂.

(2)、请直接写出以A₁、B₂、C₂为顶点的平行四边形的第四个顶点D的坐标.

查看试题解析
23. 为了促进学生多样化发展，某校组织开展了社团活动，分别设置了体育类、艺术类、文学类及其它类社团（要求人人参与社团，每人只能选择一项）．为了解学生喜爱哪种社团活动，学校做了一次抽样调查．根据收集到的数据，绘制成如下两幅不完整的统计图，请根据图中提供的信息，完成下列问题：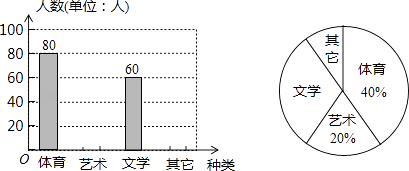

(1)、此次共调查了多少人？

(2)、求文学社团在扇形统计图中所占圆心角的度数；

(3)、请将条形统计图补充完整；

(4)、若该校有1500名学生，请估计喜欢体育类社团的学生有多少人？

查看试题解析
24. 如图所示，已知在平行四边形ABCD中，BE=DF
求证：AE=CF．

查看试题解析
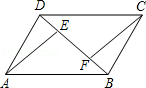25. 已知：如图，在矩形ABCD中，对角线AC与BD相交于点O，过点A作AE⊥BD，垂足为点E，若∠EAC=2∠CAD，求∠BAE的度数.

查看试题解析
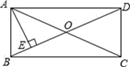26. 已知菱形的一个角与三角形的一个角重合，然后它的对角顶点在这个重合角的对边上，这个菱形称为这个三角形的亲密菱形，如图，在△CFE中，CF=6，CE=12，∠FCE=45°，以点C为圆心，以任意长为半径作AD，再分别以点A和点D为圆心，大于 $\frac{1}{2}$ AD长为半径做弧，交EF于点B，AB∥CD.

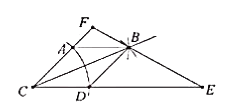(1)、求证：四边形ACDB为△CFE的亲密菱形；

(2)、求四边形ACDB的面积.

查看试题解析
27. 已知：在Rt△ABC中，∠BAC=90°，D是BC的中点，E是AD的中点.过点A做AF∥BC交BE的延长线于点F.

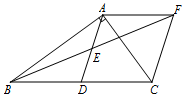(1)、求证：△AEF≌△DEB；

(2)、证明四边形ADCF是菱形；若AC=4，AB=5，求菱形ADCF的面积.

(3)、当△ABC满足什么条件时，四边形ADCF是正方形，请说明理由.

查看试题解析
28. 如图，直线 $l_{1} ： y ＝ - \frac{1}{2} x + b$ 分别与x轴、y轴交于 $A 、 B$ 两点，与直线 $l_{2} ： y ＝ k x ﹣ 6$ 交于点C（4，2）.

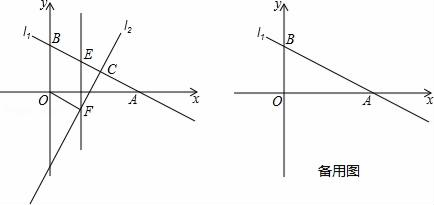(1)、点A坐标为（，），B为（，）；

(2)、在线段 $B C$ 上有一点E，过点E作y轴的平行线交直线 $l_{2}$ 于点F，设点E的横坐标为m，当m为何值时，四边形 $O B E F$ 是平行四边形；

(3)、若点P为x轴上一点，则在平面直角坐标系中是否存在一点Q，使得 $P 、 Q 、 A 、 B$ 四个点能构成一个菱形.若存在，求出所有符合条件的Q点坐标；若不存在，请说明理由.

查看试题解析