江苏省苏州市工业园区2018-2019学年八年级下学期数学期中考试试卷
试卷更新日期:2019-07-08 类型:期中考试
一、单选题
-
1. 在设计课上,老师要求学生设计一幅既是轴对称又是中心对称的图案,下面是四位同学的设计作品,其中不符合要求的是 ( )A、
 B、
B、 C、
C、 D、
D、 2. 下列各式 中,分式有( )个A、2 B、3 C、4 D、53. 顺次连接四边形四边中点所组成的四边形是菱形,则原四边形一定为 ( )A、平行四边形 B、矩形 C、对角线相等的四边形 D、等腰梯形4. 已知 是反比例函数,则该函数的图象在( )A、第一、三象限 B、第二、四象限 C、第一、二象限 D、第三、四象限5. 在反比例函数 的图像上有三点( , ),( , ),( , )若 > >0> ,则下列各式正确的是( )A、 > > B、 > > C、 > > D、 > >6. 一个直角三角形的两直角边长分别为x、y其面积为2,则y与x之间的关系用图象表示大致为 ( )A、
2. 下列各式 中,分式有( )个A、2 B、3 C、4 D、53. 顺次连接四边形四边中点所组成的四边形是菱形,则原四边形一定为 ( )A、平行四边形 B、矩形 C、对角线相等的四边形 D、等腰梯形4. 已知 是反比例函数,则该函数的图象在( )A、第一、三象限 B、第二、四象限 C、第一、二象限 D、第三、四象限5. 在反比例函数 的图像上有三点( , ),( , ),( , )若 > >0> ,则下列各式正确的是( )A、 > > B、 > > C、 > > D、 > >6. 一个直角三角形的两直角边长分别为x、y其面积为2,则y与x之间的关系用图象表示大致为 ( )A、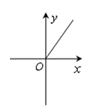 B、
B、 C、
C、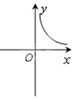 D、
D、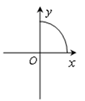 7. 菱形的周长为20 cm,两邻角的比为1:2,则较长的对角线长为 ( )A、5 cm B、4 cm C、5 cm D、4 cm8. 已知 ,则, 的值为( )A、3 B、5 C、7 D、99. 如图,□ABCD的顶点A的坐标为( ),顶点D在双曲线y= (x>0), AD交y轴于点E(0,2),且四边形BCDE的面积是△ABE面积的3倍,则k的值为 ( )
7. 菱形的周长为20 cm,两邻角的比为1:2,则较长的对角线长为 ( )A、5 cm B、4 cm C、5 cm D、4 cm8. 已知 ,则, 的值为( )A、3 B、5 C、7 D、99. 如图,□ABCD的顶点A的坐标为( ),顶点D在双曲线y= (x>0), AD交y轴于点E(0,2),且四边形BCDE的面积是△ABE面积的3倍,则k的值为 ( ) A、4 B、6 C、7 D、810. 如图,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为 ( )
A、4 B、6 C、7 D、810. 如图,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为 ( ) A、2 B、2 C、3 D、
A、2 B、2 C、3 D、二、填空题
-
11. 当x时, 有意义.12. 函数 的图象与直线y=x没有交点,那么k的取值范围是 .
13. 设函数y= 与y=x-1的图象的交点坐标为(a,b),则 的值为.
14. 若关于x的分式方程 无解,则a= .15. 已知在▱ABCD中,∠ABC的平分线交AD于点E,且AE=2,DE=1,则▱ABCD的周长等于. 16. 如图,两个反比例函数y= 和y= 在第一象限内的图象依次是C2和C1 , 设点P在C1上,PC⊥x轴于点C,交C2于点A,PD⊥y轴于点D,交C2于点B,则四边形PAOB的面积为.
16. 如图,两个反比例函数y= 和y= 在第一象限内的图象依次是C2和C1 , 设点P在C1上,PC⊥x轴于点C,交C2于点A,PD⊥y轴于点D,交C2于点B,则四边形PAOB的面积为. 17. 如图,G为正方形ABCD的边AD上的一个动点,正方形 的边长为4,AE⊥BG,CF⊥BG,垂足分别为点E,F,则AE2+CF2=.
17. 如图,G为正方形ABCD的边AD上的一个动点,正方形 的边长为4,AE⊥BG,CF⊥BG,垂足分别为点E,F,则AE2+CF2=. 18. 如图,A,B两点的坐标分别为(6,0),(0,6),点P从点A出发,沿AB方向以每秒 个单位的速度向终点B运动;同时动点Q从点B出发沿BO方向以每秒1个单位的速度向终点Q运动,将△PQO沿BO翻折,点P的对应点为点C,若四边形QPOC为菱形,则点C的坐标为.
18. 如图,A,B两点的坐标分别为(6,0),(0,6),点P从点A出发,沿AB方向以每秒 个单位的速度向终点B运动;同时动点Q从点B出发沿BO方向以每秒1个单位的速度向终点Q运动,将△PQO沿BO翻折,点P的对应点为点C,若四边形QPOC为菱形,则点C的坐标为.
三、解答题
-
19.(1)、(2)、20. 解方程:(1)、(2)、21. 若 = + ,求A、B的值.22. 一次函数y=2x-2的图像与反比例函数y= 的图像交于点M(2,a)与N(b,-4)两点。(1)、求反比例函数的解析式.(2)、画出草图,根据图像写出反比例函数的值大于一次函数的值时的x的取值范围.(3)、求△MON的面积.23. 某服装厂设计了一款新式夏装,想尽快制作8 800件投入市场, 服装厂有A、B两个制衣车间,A车间每天加工的数量是B车间的1.2倍,A、B两个车间共同完成一半后,A车间出现故障停产,剩下的全部由B车间单独完成,结果前后共用了20天完成.A、B两个车间每天分别能加工多少件?24. 如图,在四边形ABCD中,E、F分别是AD、BC的中点,G、H分别是BD、AC的中点且AB=CD,则EF与GH有怎样的关系?请说明你的理由.
 25. 将两张完全相同的矩形纸片ABCD、FBED按如图方式放置,BD为重合的对角线.重叠部分为四边形DHBG,
25. 将两张完全相同的矩形纸片ABCD、FBED按如图方式放置,BD为重合的对角线.重叠部分为四边形DHBG,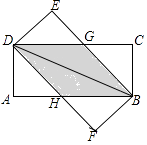 (1)、试判断四边形DHBG为何种特殊的四边形,并说明理由;(2)、若AB=8,AD=4,求四边形DHBG的面积.26. 如图,直线 与双曲线 交于点A、E,AB交双曲线于另一点B( , ),连接EB并延长交x轴于点F.
(1)、试判断四边形DHBG为何种特殊的四边形,并说明理由;(2)、若AB=8,AD=4,求四边形DHBG的面积.26. 如图,直线 与双曲线 交于点A、E,AB交双曲线于另一点B( , ),连接EB并延长交x轴于点F. (1)、 ;(2)、求直线AB的解析式;(3)、求△EOF的面积;(4)、若点P为坐标平面内一点,且以A,B,E,P为顶点的四边形是平行四边形,请直接写出点P的坐标.27. 如图,正方形ABCO的边OA、OC在坐标轴上,点B的坐标为(6,6),将正方形ABCO绕点C逆时针旋转角度α(0°<α<90°),得到正方形CDEF,ED交线段AB于点G,ED的延长线交线段OA于点H,连接CH、CG.
(1)、 ;(2)、求直线AB的解析式;(3)、求△EOF的面积;(4)、若点P为坐标平面内一点,且以A,B,E,P为顶点的四边形是平行四边形,请直接写出点P的坐标.27. 如图,正方形ABCO的边OA、OC在坐标轴上,点B的坐标为(6,6),将正方形ABCO绕点C逆时针旋转角度α(0°<α<90°),得到正方形CDEF,ED交线段AB于点G,ED的延长线交线段OA于点H,连接CH、CG. (1)、求证:△CBG≌△CDG;(2)、求∠HCG的度数;并判断线段HG、OH、BG之间的数量关系,说明理由;(3)、连接BD、DA、AE、EB得到四边形AEBD,在旋转过程中,四边形AEBD能否为矩形?如果能,请求出点H的坐标;如果不能,请说明理由.
(1)、求证:△CBG≌△CDG;(2)、求∠HCG的度数;并判断线段HG、OH、BG之间的数量关系,说明理由;(3)、连接BD、DA、AE、EB得到四边形AEBD,在旋转过程中,四边形AEBD能否为矩形?如果能,请求出点H的坐标;如果不能,请说明理由.