江苏省如皋市白蒲镇2018-2019学年八年级下学期数学期中考试试卷
试卷更新日期:2019-07-08 类型:期中考试
一、单选题
-
1. 函数y=−3x+4, y= x , y=1+ , y=x2+2中,一次函数的个数为 ( )A、1个 B、2个 C、3个 D、4个2. 某专卖店专营某品牌的衬衫,店主对上一周中不同尺码的衬衫销售情况统计如下:
尺码
39
40
41
42
43
平均每天销售数量/件
6
15
21
12
9
该店主决定本周进货时,增加了一些41码的衬衫,影响该店主决策的统计量是( )
A、平均数 B、中位数 C、方差 D、众数3. 关于一次函数y=﹣2x+3,下列结论正确的是( )A、图象过点(1,﹣1) B、图象经过一、二、三象限 C、y随x的增大而增大 D、当x> 时,y<04. 顺次连接菱形各边中点所形成的四边形是( )
A、平行四边形 B、菱形 C、 矩形 D、正方形5. 如图,矩形ABCD的对角线AC=8 cm, ,则AB的长为( ) A、 cm B、2cm C、4cm D、 cm6. 在平行四边形ABCD中添加下列条件,不能判定四边形ABCD是矩形的是( )A、 90° B、AC BD C、AC=BD D、7. 已知函数y=kx+b的图象如图所示,则函数y=-bx+k的图象大致是( )
A、 cm B、2cm C、4cm D、 cm6. 在平行四边形ABCD中添加下列条件,不能判定四边形ABCD是矩形的是( )A、 90° B、AC BD C、AC=BD D、7. 已知函数y=kx+b的图象如图所示,则函数y=-bx+k的图象大致是( )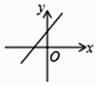 A、
A、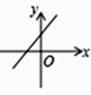 B、
B、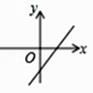 C、
C、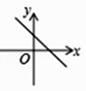 D、
D、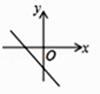 8. 均匀地向一个容器注水,最后把容器注满,在注水过程中,水面高度h随时间t的变化规律如图所示(图中OABC为折线),这个容器的形状可以是( )
8. 均匀地向一个容器注水,最后把容器注满,在注水过程中,水面高度h随时间t的变化规律如图所示(图中OABC为折线),这个容器的形状可以是( ) A、
A、 B、
B、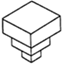 C、
C、 D、
D、 9. 已知一次函数y=kx+b,当−3<x<1时,对应的y值为−1<y<3,则b的值是( )A、2 B、3或0 C、3 D、2或010. 如图,P为线段AB上的一个点,分别以AP,PB为边在AB的同侧作菱形APCD和菱形PBFE,点P,C,E在一条直线上。若∠DAP=60°,AP2+3PB2=1, M,N分别是对角线AC,BE的中点. MN长为( )
9. 已知一次函数y=kx+b,当−3<x<1时,对应的y值为−1<y<3,则b的值是( )A、2 B、3或0 C、3 D、2或010. 如图,P为线段AB上的一个点,分别以AP,PB为边在AB的同侧作菱形APCD和菱形PBFE,点P,C,E在一条直线上。若∠DAP=60°,AP2+3PB2=1, M,N分别是对角线AC,BE的中点. MN长为( )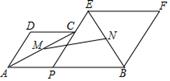 A、 B、 C、1 D、4
A、 B、 C、1 D、4二、填空题
-
11. 直线y=-2x-6与两坐标轴围成的三角形的面积为.12. 小华的平时测验成绩是80分,期中考试成绩是85分,期末考试成绩是90分.若按平时、期中、期末之比为1:2:7计算总评成绩,则他的总评成绩是 分
13. 如图,一次函数y1=x+b与一次函数y2=kx+4的图象交于点P(1,3),则关于x的不等式x+b>kx+4的解集是.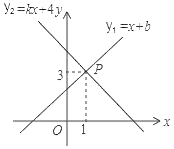 14. 如图,▱ABCD的对角线AC,BD相交于点O,且AC+BD=16,CD=6,则△ABO的周长是.
14. 如图,▱ABCD的对角线AC,BD相交于点O,且AC+BD=16,CD=6,则△ABO的周长是. 15. 如图,矩形ABCD中,点E在边AB上,将矩形ABCD沿直线DE折叠,点A恰好落在边BC的点F处。若AE=10,BF=6,则CD的长是.
15. 如图,矩形ABCD中,点E在边AB上,将矩形ABCD沿直线DE折叠,点A恰好落在边BC的点F处。若AE=10,BF=6,则CD的长是. 16. 直线y=−2x+m与直线y=2x−1的交点在第四象限,则m的取值范围是.17. 正方形ABCD中,E为DC边上一点,且DE=1,将AE绕点E逆时针旋转90度,得到EF,连接AF,FC,则FC=.
16. 直线y=−2x+m与直线y=2x−1的交点在第四象限,则m的取值范围是.17. 正方形ABCD中,E为DC边上一点,且DE=1,将AE绕点E逆时针旋转90度,得到EF,连接AF,FC,则FC=. 18. △ABC中,AB=AC=13,BC=24,点P是BC边上的动点,过点P作PD⊥AB于点D,则PD+PE的长是.
18. △ABC中,AB=AC=13,BC=24,点P是BC边上的动点,过点P作PD⊥AB于点D,则PD+PE的长是.三、解答题
-
19. 已知y−3与4x−2成正比例,且当x=1时,y=5.(1)、求y与x的函数关系式;(2)、求当x=−2时的函数值;(3)、如果y的取值范围是0≤y≤5,求x的取值范围.20. 我市某中学举行“中国梦⋅校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛。两个队各选出的5名选手的决赛成绩如图所示.
 (1)、根据图示填写下表;
(1)、根据图示填写下表;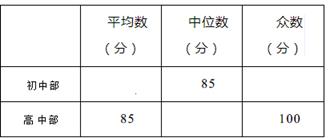 (2)、结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;(3)、计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.21. 如图,直线 的解析表达式为:y=-3x+3,且 与x轴交于点D,直线 经过点A,B,直线 , 交于点C.
(2)、结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;(3)、计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.21. 如图,直线 的解析表达式为:y=-3x+3,且 与x轴交于点D,直线 经过点A,B,直线 , 交于点C.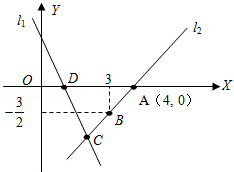 (1)、求点D的坐标;(2)、求直线 的解析表达式;(3)、求△ADC的面积;(4)、在直线 上存在异于点C的另一点P,使得△ADP的面积是△ADC面积的2倍,请直接写出点P的坐标.22. 如图,AE∥BF,AC平分∠BAE,交BF于点C,BD平分∠ABC,交AE于点D,连接CD.
(1)、求点D的坐标;(2)、求直线 的解析表达式;(3)、求△ADC的面积;(4)、在直线 上存在异于点C的另一点P,使得△ADP的面积是△ADC面积的2倍,请直接写出点P的坐标.22. 如图,AE∥BF,AC平分∠BAE,交BF于点C,BD平分∠ABC,交AE于点D,连接CD. (1)、求证:四边形ABCD是菱形;(2)、若AB=5,AC=6,求AE,BF之间的距离.23. 小明购买A,B两种商品,每次购买同一种商品的单价相同,具体信息如下表:
(1)、求证:四边形ABCD是菱形;(2)、若AB=5,AC=6,求AE,BF之间的距离.23. 小明购买A,B两种商品,每次购买同一种商品的单价相同,具体信息如下表:次数
购买数量(件
购买总费用(元
A
B
第一次
2
1
55
第二次
1
3
65
根据以上信息解答下列问题:
(1)、求A,B两种商品的单价;(2)、若第三次购买这两种商品共12件,且A种商品的数量不少于B种商品数量的2倍,请设计出最省钱的购买方案,并说明理由.24. 如图,矩形ABCD中,点P是线段AD上的一个动点,O为BD的中点,PO的延长线交BC于Q. (1)、求证:OP=OQ ;(2)、若AD=8cm,AB=6cm,点P从点A出发,以 的速度向点D 运动(不与D重合).设点P运动的时间为t秒,请用t表示PD的长;(3)、当t为何值时,四边形PBQD是菱形?25. 学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地.两人之间的距离y(米)与时间t(分钟)之间的函数关系如图所示.
(1)、求证:OP=OQ ;(2)、若AD=8cm,AB=6cm,点P从点A出发,以 的速度向点D 运动(不与D重合).设点P运动的时间为t秒,请用t表示PD的长;(3)、当t为何值时,四边形PBQD是菱形?25. 学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地.两人之间的距离y(米)与时间t(分钟)之间的函数关系如图所示. (1)、根据图象信息,当t=分钟时甲乙两人相遇,甲的速度为米/分钟;(2)、求出线段AB所表示的函数表达式.26. (问题情境)
(1)、根据图象信息,当t=分钟时甲乙两人相遇,甲的速度为米/分钟;(2)、求出线段AB所表示的函数表达式.26. (问题情境)如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.
(探究展示)
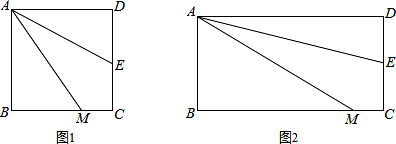 (1)、证明:AM=AD+MC;(2)、AM=DE+BM是否成立?若成立,请给出证明;若不成立,请说明理由.(3)、若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,探究展示(1)、(2)中的结论是否成立?请分别作出判断,不需要证明.
(1)、证明:AM=AD+MC;(2)、AM=DE+BM是否成立?若成立,请给出证明;若不成立,请说明理由.(3)、若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,探究展示(1)、(2)中的结论是否成立?请分别作出判断,不需要证明.