湖北省十堰市2018-2019学年七年级下学期数学期末考试试卷

试卷更新日期：2019-07-08 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各数中是无理数的是（）

A、 $\sqrt{2}$ B、 $\sqrt{4}$ C、 $\sqrt[3]{27}$ D、3.14

查看试题解析
2. 已知 $x > y$ ，下列变形正确的是（）

A、 $x - 1 < y - 1$ B、 $2 x + 1 < 2 y + 1$ C、 $- x < - y$ D、 $\frac{x}{2} < \frac{y}{2}$

查看试题解析
3. 下列调查中，适合抽样调查的是（）

A、了解某班学生的身高情况 B、检测十堰城区的空气质量 C、选出某校短跑最快的学生参加全市比赛 D、全国人口普查

查看试题解析
4. 含30°角的直角三角板与直线a，b的位置关系如图所示，已知a∥b，∠1=40°，则∠ADC的度数是（）

A、40° B、45° C、50° D、60°

查看试题解析
5. 下列命题属于真命题的是（）

A、同旁内角相等，两直线平行 B、相等的角是对顶角 C、平行于同一条直线的两条直线平行 D、同位角相等

查看试题解析
6. 若点P（a，4﹣a）是第二象限的点，则a必须满足（）

A、a＜0 B、a＜4 C、0＜a＜4 D、a＞4

查看试题解析
7. 某超市销售一批创意闹钟，先以55元 $/$ 个的价格售出60个，然后调低价格，以50元 $/$ 个的价格将剩下的闹钟全部售出，销售总额超过了5500元，这批闹钟至少有 $($ $)$ 个.

A、44 B、45 C、104 D、105

查看试题解析
8. 《孙子算经》中有一道题，原文是：“今有木，不知长短.引绳度之，余绳四尺五寸；屈绳量之，不足一尺.木长几何？”意思是：用一根绳子去量一根长木，绳子还剩余4.5尺；将绳子对折再量长木，长木还剩余1尺，问木长多少尺？设木长为x尺，绳子长为y尺，则下列正确的方程组是（）

A、 ${\begin{array}{l} y = x + 4.5 \\ \frac{1}{2} y = x + 1 \end{array}$ B、 ${\begin{array}{l} y = x - 4.5 \\ \frac{1}{2} y = x + 1 \end{array}$ C、 ${\begin{array}{l} y = x - 4.5 \\ \frac{1}{2} y = x - 1 \end{array}$ D、 ${\begin{array}{l} y = x + 4.5 \\ \frac{1}{2} y = x - 1 \end{array}$

查看试题解析
9. 如图已知∠1＝∠2，∠BAD＝∠BCD，则下列结论：①AB∥CD，②AD∥BC，③∠B＝∠D，④∠D＝∠ACB，正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 将正整数按如图所示的规律排列下去，若有序数对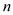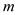（，）表示第n排，从左到右第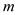个数，如（4，2）表示9，则表示114的有序数对是（）

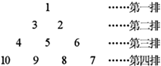A、（15，9） B、（9，15） C、（15，7） D、（7，15）

查看试题解析

二、填空题

11. P（3，﹣4）到x轴的距离是．

查看试题解析
12. 为了直观地表示我国体育健儿在最近六届夏季奥运会上获得奖牌总数的变化趋势，最适合使用的统计图是.（从“扇形图”、“折线图”、“条形图”、“直方图”中选填）

查看试题解析
13. 如图，有一条平直的等宽纸带按图折叠时，则图中∠α=

查看试题解析
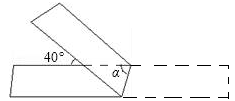14. 对于有理数a，b，定义min{a，b}的含义为：当a＜b时，min{a，b}＝a，例如：min{1，－2}＝－2.已知min{ $\sqrt{21}$ ，a}＝ $\sqrt{21}$ ，min{ $\sqrt{21}$ ，b}＝b，且a和b为两个连续正整数，则a－b的平方根为.

查看试题解析

三、解答题

15. 计算下列各式的值：

(1)、 $\sqrt[3]{8} - 4 - | \sqrt{3} - 2 | + \sqrt{16}$ ；

(2)、 $3 (\sqrt{3} + \sqrt{2}) - 2 (\sqrt{3} - \sqrt{2})$ .

查看试题解析
16. 解下列方程组：

(1)、 ${\begin{array}{l} x = 1 - 3 y, \\ 3 x - y = 3; \end{array}$

(2)、 ${\begin{array}{l} 3 x - 4 y = 9, \\ 2 x - 3 y = 7. \end{array}$

查看试题解析
17. 解不等式组 ${\begin{array}{l} x - 3 (x - 2) \geq 4， \\ \frac{1 + 4 x}{3} > x - 1 \end{array}$ ，并把解集在数轴上表示出来.

查看试题解析
18. 某学校准备开展“阳光体育活动”，决定开设以下体育活动项目：足球、乒乓球、篮球和羽毛球，要求每位学生必须且只能选择一项，为了解选择各种体育活动项目的学生人数，随机抽取了部分学生进行调查，并将获得的数据进行整理，绘制出两幅不完整的统计图，请根据统计图回答问题.

(1)、这次活动一共调查了名学生；

(2)、补全条形统计图；

(3)、在扇形统计图中，选择篮球项目的人数所在扇形的圆心角等于度；

(4)、若该学校有1000人，请你估计该学校选择乒乓球项目的学生人数约是人.

查看试题解析
19. 在平面直角坐标系xOy中，△ABC的三个顶点分别是A（-2，0），B（0，3），C（3，0）.

①在所给的图中，画出这个平面直角坐标系；

②点A经过平移后对应点为D（3，-3），将△ABC作同样的平移得到△DEF，点B的对应点为点E，画出平移后的△DEF；

③在（2）的条件下，点M在直线CD上，若DM=2CM，直接写出点M的坐标.

查看试题解析
20. 在长为20 m、宽为16 m的长方形空地上，沿平行于长方形各边的方向割出三个完全相同的小长方形花圃，其示意图如图所示，求每个小长方形花圃的面积.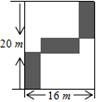

查看试题解析
21. 如图，点O在直线AB上，OC⊥OD，∠EDO与∠1互余.

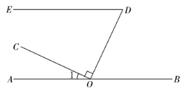(1)、求证：ED//AB；

(2)、OF平分∠COD交DE于点F，若∠OFD=65^° ，补全图形，并求∠1的度数.

查看试题解析
22. 先阅读下列一段文字，再解答问题：
已知在平面内有两点 $P_{1} (x_{1} ， y_{1})$ ， $P_{2} (x_{2} ， y_{2})$ ，其两点间的距离公式为 $P_{1} P_{2} = \sqrt{{(x_{2} - x_{1})}^{2} + {(y_{2} - y_{1})}^{2}}$ ；同时，当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时，两点间距离公式可简化为 $| x_{2} - x_{1} |$ 或 $| y_{2} - y_{1} |$ .

(1)、已知点A（2，4），B（-2，1），则AB=；

(2)、已知点C，D在平行于y轴的直线上，点C的纵坐标为4，点D的纵坐标为-2，则CD=；

(3)、已知点P（3，1）和（1）中的点A，B，判断线段PA，PB，AB中哪两条线段的长是相等的？并说明理由.

查看试题解析

23. 某超市销售每台进价分别为180元、150元的甲、乙两种型号的电器，下表是近两周的销售情况：

销售时段	销售数量		销售收入
销售时段	甲种型号	乙种型号	销售收入
第一周	2台	3台	1100元
第二周	4台	5台	2000元

（进价、售价均保持不变，利润=销售收入-进货成本）

(1)、求甲、乙两种型号的电器的销售单价；

(2)、若超市准备用不多于5000元的金额再采购这两种型号的电器共30台，求甲种型号的电器最多能采购多少台？

(3)、在（2）的条件下，超市销售完这30台电器能否实现利润超过1900元的目标？若能，请给出相应的采购方案；若不能，请说明理由.

查看试题解析

24. 已知：如图（1），如果AB∥CD∥EF. 那么∠BAC+∠ACE+∠CEF=360°.
老师要求学生在完成这道教材上的题目后，尝试对图形进行变式，继续做拓展探究，看看有什么新发现？

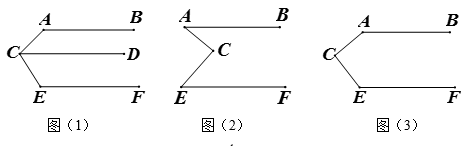
(1)、小华首先完成了对这道题的证明，在证明过程中她用到了平行线的一条性质，小华用到的平行线性质可能是.

(2)、接下来，小华用《几何画板》对图形进行了变式，她先画了两条平行线AB，EF，然后在平行线间画了一点C，连接AC，EC后，用鼠标拖动点C，分别得到了图（2）（3）（4），小华发现图（3）正是上面题目的原型，于是她由上题的结论猜想到图（2）和（4）中的∠BAC，∠ACE与∠CEF之间也可能存在着某种数量关系.然后，她利用《几何画板》的度量与计算功能，找到了这三个角之间的数量关系.
请你在小华操作探究的基础上，继续完成下面的问题：

①猜想：图（2）中∠BAC，∠ACE与∠CEF之间的数量关系：.

②补全图（4），并直接写出图中∠BAC，∠ACE与∠CEF之间的数量关系：.

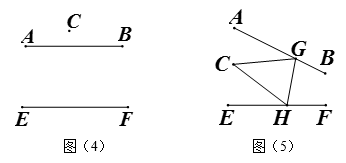
(3)、小华继续探究：如图（5），若直线AB与直线EF不平行，点G，H分别在直线AB、直线EF上，点C在两直线外，连接CG，CH，GH，且GH同时平分∠BGC和∠FHC，请探索∠AGC，∠GCH与∠CHE之间的数量关系？并说明理由.

查看试题解析