江苏省苏州市区2018-2019学年七年级下学期数学期末考试试卷
试卷更新日期:2019-07-08 类型:期末考试
一、单选题
-
1. 下列运算中,正确的是( )A、 B、 C、 D、2. 若 ,则下列判断中错误的是( )A、 B、 C、 D、3. 不等式组 的解集在数轴上可以表示为( )A、
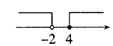 B、
B、 C、
C、 D、
D、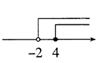 4. 已知 是二元一次方程 的一个解,则 的值为( )A、3 B、-5 C、-3 D、55. 下列命题中真命题的是( )A、同旁内角互补 B、三角形的一个外角等于两个内角的和 C、若 ,则 D、同角的余角相等6. 如图,已知 ,添加条件后,可得 ,则在下列条件中,不能添加的是( )
4. 已知 是二元一次方程 的一个解,则 的值为( )A、3 B、-5 C、-3 D、55. 下列命题中真命题的是( )A、同旁内角互补 B、三角形的一个外角等于两个内角的和 C、若 ,则 D、同角的余角相等6. 如图,已知 ,添加条件后,可得 ,则在下列条件中,不能添加的是( )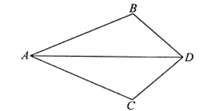 A、 B、 C、 D、7. 若33×9m=311 ,则m的值为 ( )A、2 B、3 C、4 D、58. 若 是一个完全平方式,则 的值为( )A、±4 B、±2 C、4 D、-49. 若一个多边形的内角和等于外角和的2倍,则这个多边形的边数为A、8 B、6 C、5 D、410. 若 , ,则 与 的关系为( )A、 B、 C、 D、 与 的大小由 的取值而定
A、 B、 C、 D、7. 若33×9m=311 ,则m的值为 ( )A、2 B、3 C、4 D、58. 若 是一个完全平方式,则 的值为( )A、±4 B、±2 C、4 D、-49. 若一个多边形的内角和等于外角和的2倍,则这个多边形的边数为A、8 B、6 C、5 D、410. 若 , ,则 与 的关系为( )A、 B、 C、 D、 与 的大小由 的取值而定二、填空题
-
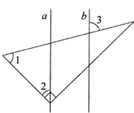
11. 肥皂泡的泡壁厚度大约是 , 用科学记数法表示为 .12. 若 ,则 = .13. 已知 ,若用含 的代数式表示 ,则 =.14. 若 ,则代数式 的值等于.15. 如图, ,将三角尺的直角顶点落在直线 上,若 , ,则 =.
 16. 若方程组 的解为 ,则方程组 的解为 .17. 如图,四边形 中,点 分别在 上,将 沿 翻折,得 ,若 ,则 =.
16. 若方程组 的解为 ,则方程组 的解为 .17. 如图,四边形 中,点 分别在 上,将 沿 翻折,得 ,若 ,则 =.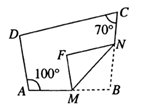 18. 如图, 中, .点 从点 出发沿 路径向终点 运动;点 从 点出发沿 路径向终点 运动.点 和 分别以1和3的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过 和 作 于 , 于 .则点 运动时间等于时, 与 全等。
18. 如图, 中, .点 从点 出发沿 路径向终点 运动;点 从 点出发沿 路径向终点 运动.点 和 分别以1和3的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过 和 作 于 , 于 .则点 运动时间等于时, 与 全等。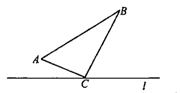
三、解答题
-
19. 计算:(1)、(2)、20. 因式分解:(1)、(2)、21.(1)、解方程组:(2)、求不等式 的最大整数解.22. 先化简,再求值: 其中 .23. 画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.
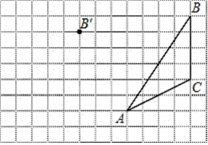
①在给定方格纸中画出平移后的△A′B′C′;
②画出AB边上的中线CD
③画出BC边上的高线AE
④点 为方格纸上的格点(异于点 ),若 ,则图中的格点 共有 个.
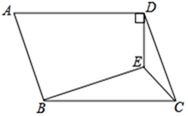
24. 如图,四边形ABCD内有一点E,AD//BC,满足ED⊥AD,且∠EBC=∠EDC,BE=CD.证明:∠ECB=45°.
 25. 某校计划组织师生共435人参加一次大型公益活动,如果租用5辆小客车和6辆大客车恰好全部坐满,已知每辆大客车的乘客座位数比小客车多12个.(1)、求每辆小客车和每辆大客车的乘客座位数;(2)、由于最后参加活动的人数增加了20人,学校决定调整租车方案,在保持租用车辆总数不变的情况下,为将所有参加活动的师生装载完成,求租用小客车数量的最大值.
25. 某校计划组织师生共435人参加一次大型公益活动,如果租用5辆小客车和6辆大客车恰好全部坐满,已知每辆大客车的乘客座位数比小客车多12个.(1)、求每辆小客车和每辆大客车的乘客座位数;(2)、由于最后参加活动的人数增加了20人,学校决定调整租车方案,在保持租用车辆总数不变的情况下,为将所有参加活动的师生装载完成,求租用小客车数量的最大值.
