浙江省宁波市余姚市2018-2019学年七年级下学期数学期末考试试卷
试卷更新日期:2019-07-08 类型:期末考试
一、选择题(本题有12小题,每小题3分,共36分)
-
1. 下列各组数中,是二元一次方程2x-3y=1的解的是( )A、 B、 C、 D、2. 下列计算正确的是( )A、a4-a2=a2 B、a4÷a2=a2 C、a4+a2=a6 D、a4·a2=a83. 为了解本校学生课外使用网络情况,学校采用抽样问卷调查,下面的抽样方法最恰当的是( )A、随机抽取七年级5位同学 B、随机抽取七年级每班各5位同学 C、随机抽取全校5位同学 D、随机抽取全校每班各5位同学4. 已知∠1和∠2是同旁内角.若∠1=40°,则∠2的度数是( )A、40° B、140° C、160° D、无法确定5. 已知1纳米等于0.000 000 001米,那么2纳米用科学记数法表示为( )A、2×10-9米 B、0.2×10-8米 C、20×108米 D、2×109米6. 如图是某手机店今年1-5月份某品牌手机销售额的统计图,根据图中信息,可以判断相邻两个月该品牌手机销售额变化最大的是( )

A、1月至2月 B、2月至3月 C、3月至4月 D、4月至5月7. 下列等式不正确的是( )A、(a+b)(a-b)=a2-b2 B、(a+b)(-a-b)=-(a+b)2 C、(a-b)(-a+b)=-(a-b)2 D、(a-b)(-a-b)=-a2-b28. 已知在同一平面内有三条不同的直线a,b,c,下列说法错误的是( )A、如果a∥b,a⊥c,那么b⊥c B、如果b∥a,c∥a,那么b∥c C、如果b⊥a,c⊥a,那么b⊥c D、如果b⊥a,c⊥a,那么b∥c9. 要使分式 有意义,则实数x的取值应满足( )A、x≠0 B、x≠1 C、x≠0或x≠1 D、x≠0且x≠110. 若(x+2y)2=(x-2y)2+A,则A等于( )A、8xy B、-8xy C、8y2 D、4xy11. 多项式4a2+1再加上一个单项式后,使其成为一个多项式的完全平方,则不同的添加方法有( )A、2种 B、3种 C、4种 D、多于4种12. 如图,平行河岸两侧各有一城镇P,Q,根据发展规划,要修建一条公路连接P,Q两镇.已知相同长度造桥总价远大于陆上公路造价,为了尽量减少总造价,应该选择方案( )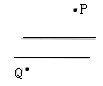 A、
A、 B、
B、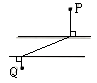 C、
C、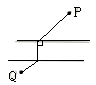 D、
D、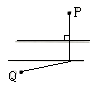
二、填空题(本题有6小题,每小题3分,共18分)
-
13. 计算:(-2)0+(-2)-1=。14. 分式 与 的最简公分母为 。15. 如图,将一条两边沿互相平行的纸带折叠.若∠1=44°,则∠a=。
 16. 因式分解:3a3-12a= 。17. 已知关于x,y的方程组 的解是 ,则a2-b2的值为。18. 如图,一副三角板的三个内角分别是90,45°,45°和90°,60°,30°,按如图所示叠放在一起(点A,D,B在同一直线上).若固定△ABC,将△BDE绕着公共顶点B顺时针旋转a度(0<a<180),当边DE与△ABC的某一边平行时,相应的旋转角a的值为 。
16. 因式分解:3a3-12a= 。17. 已知关于x,y的方程组 的解是 ,则a2-b2的值为。18. 如图,一副三角板的三个内角分别是90,45°,45°和90°,60°,30°,按如图所示叠放在一起(点A,D,B在同一直线上).若固定△ABC,将△BDE绕着公共顶点B顺时针旋转a度(0<a<180),当边DE与△ABC的某一边平行时,相应的旋转角a的值为 。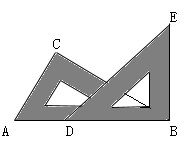
三、解答题(第19题6分,第20题8分,第21题6分,第22、23、24题各8分,第25题10分,第26题12分,共66分)
-
19. 计算:(1)、(2a2)3÷a3(2)、(2m+1)(m-2)-2m(m-2)20. 解方程(组):(1)、(2)、21. 先化简,再求值:
,其中x=
22. 如图,点D在△ABC的边AC上,过点D作DE∥BC交AB于E,作DF∥AB交BC于F (1)、请按题意补全图形(2)、请判断∠EDF与∠B的大小关系,并说明理由23. 为了解某校学生的身高情况,随机抽取该校男生、女生进行调查,已知抽取的样本中,男生和女生的人数相同,利用所得数据绘制如下统计图表:
(1)、请按题意补全图形(2)、请判断∠EDF与∠B的大小关系,并说明理由23. 为了解某校学生的身高情况,随机抽取该校男生、女生进行调查,已知抽取的样本中,男生和女生的人数相同,利用所得数据绘制如下统计图表:身高情况分组表(单位:cm)
组别
身高
A
x<155
B
155≤x<160
C
160≤x<165
D
165≤x<170
E
x≥170

根据图表提供的信息,回答下列问题:
(1)、求样本中男生的人数(2)、求样本中女生身高在E组的人数(3)、已知该校共有男生380人,女生320人,请估计全校身高在1605≤x<170之间的学生总人数。24. 某工厂承接了一批纸箱加工任务,用如图1所示的长方形和正方形纸板(长方形的宽与正方形的边长相等)作侧面和底面,加工成如图2所示的竖式和横式两种无盖的长方体纸箱.(加工时接缝材料不计)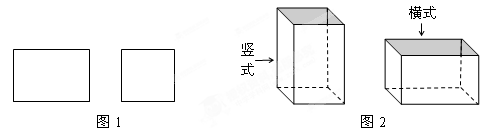 (1)、若该厂仓库里有1000张正方形纸板和2000张长方形纸板.问竖式和横式纸箱各加工多少个,恰好将库存的两种纸板全部用完?(2)、该工厂原计划用若干天加工纸箱2400个,后来由于对方急需要货,实际加工时每天加工速度是原计划的1.5倍,这样提前2天完成了任务,问原计划每天加工纸箱多少个?25. 如图,将几个小正方形与小长方形拼成一个边长为(a+b+c)的正方形
(1)、若该厂仓库里有1000张正方形纸板和2000张长方形纸板.问竖式和横式纸箱各加工多少个,恰好将库存的两种纸板全部用完?(2)、该工厂原计划用若干天加工纸箱2400个,后来由于对方急需要货,实际加工时每天加工速度是原计划的1.5倍,这样提前2天完成了任务,问原计划每天加工纸箱多少个?25. 如图,将几个小正方形与小长方形拼成一个边长为(a+b+c)的正方形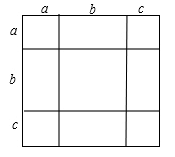 (1)、若用不同的方法计算这个边长为(a+b+c)的正方形面积,就可以得到一个等式,这个等式可以为 .(只要写出一个即可)(2)、请利用(1)中的等式解答下列问题:
(1)、若用不同的方法计算这个边长为(a+b+c)的正方形面积,就可以得到一个等式,这个等式可以为 .(只要写出一个即可)(2)、请利用(1)中的等式解答下列问题:①若三个实数a,b,c满足a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值
②若三个实数x,y,z满足2x×4y÷8z= ,x2+4y2+9z2=44,求2xy-3xz-6yz的值
26. 阅读下列材料:对于多项式x2+x-2,如果我们把x=1代入此多项式,发现x2+x-2的值为0,这时可以确定多项式中有因式(x-1):同理,可以确定多项式中有另一个因式(x+2),于是我们可以得到:x2+x-2=(x-1)(x+2)
又如:对于多项式2x2-3x-2,发现当x=2时,2x2-3x-2的值为0,则多项式2x2-3x-2有一个因式(x-2),我们可以设2x2-3x-2=(x-2)(mx+n),解得m=2,n=1,于是我们可以得到:2x2-3x-2=(x-2)(2x+1)
请你根据以上材料,解答以下问题:
(1)、当x=时,多项式6x2-x-5的值为0,所以多项式6x2-x-5有因式 ,从而因式分解6x2-x-5=.(2)、以上这种因式分解的方法叫试根法,常用来分解一些比较复杂的多项式.请你尝试用试根法分解多项式:①2x2+5x+3;②x3-7x+6(3)、小聪用试根法成功解决了以上多项式的因式分解,于是他猜想:代数式(x-2)3-(y-2)3-(x-y)3有因式 , , ,所以分解因式(x-2)3-(y-2)3-(x-y)3= 。