江苏省海安县八校联考2018-2019学年八年级下学期数学期中考试试卷

试卷更新日期：2019-07-05 类型：期中考试

进入出卷网下载

一、单选题

1. 函数 $y = \frac{1}{x - 1}$ 中，自变量x的取值范围是（）

A、x≠0 B、x＜1 C、x＞1 D、x≠1

查看试题解析
2. 下列计算正确的是（）

A、 $\sqrt{7} - \sqrt{2} = \sqrt{5}$ B、 $\sqrt{18} \div \sqrt{3} = \sqrt{6}$ C、 $\sqrt{4} \times \sqrt{6} = 4 \sqrt{6}$ D、 $\sqrt{{(- 15)}^{2}}$ ＝±15

查看试题解析
3. 已知三角形三边长为a，b，c，如果 $\sqrt{a - 6}$ +|b﹣8|+（c﹣10）²＝0，则△ABC是（）

A、以a为斜边的直角三角形 B、以b为斜边的直角三角形 C、以c为斜边的直角三角形 D、不是直角三角形

查看试题解析
4. 在四边形ABCD中，O是对角线的交点，能判定这个四边形是正方形的条件是（）

A、AC=BD，AB∥CD，AB=CD B、AD∥BC，∠A=∠C C、AO=BO=CO=DO，AC⊥BD D、AO=CO，BO=DO，AB=BC

查看试题解析
5. 对一次函数y＝﹣2x+4，下列结论正确的是（）

A、图象经过一、二、三象限 B、y随x的增大而增大 C、图象必过点（﹣2，0） D、图象与y＝﹣2x+1图象平行

查看试题解析
6. 直线y＝ $\frac{1}{2}$ x﹣1关于x轴对称的直线解析式为（）

A、y＝﹣ $\frac{1}{2}$ x﹣1 B、y＝ $\frac{1}{2}$ x+1 C、y＝﹣ $\frac{1}{2}$ x+1 D、y＝﹣2x﹣1

查看试题解析
7. 如图，△ABC中，∠C＝90°，∠A＝30°，AB＝12，则BC＝（）

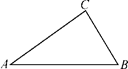A、6 B、6 $\sqrt{2}$ C、6 $\sqrt{3}$ D、12

查看试题解析
8. 如图，已知直线y₁：y＝kx+b与直线y₂：y＝mx+n相交于P（﹣3，2），则关于x不等式mx+n≤kx+b的解集为（）

A、x≤﹣3 B、x≥﹣3 C、x≤2 D、x≥2

查看试题解析
9. 如图，在矩形ABCD中，E是BC边的中点，将△ABE沿AE所在的直线折叠得到△AFE，延长AF交CD于点G，已知CG=2，DG=1，则BC的长是（）

A、 $3 \sqrt{2}$ B、 $2 \sqrt{6}$ C、 $2 \sqrt{5}$ D、 $2 \sqrt{3}$

查看试题解析
10. 甲、乙两车从A地出发，匀速驶向B地.甲车以80km/h的速度行驶1h后，乙车才沿相同路线行驶.乙车先到达B地并停留1h后，再以原速按原路返回，直至与甲车相遇.在此过程中，两车之间的距离y（km）与乙车行驶时间x（h）之间的函数关系如图所示.下列说法：①乙车的速度是120km/h；②m＝160；③点H的坐标是（7，80）；④n＝7.5.其中说法正确的是（）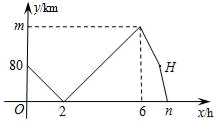

A、①②③ B、①②④ C、①③④ D、①②③④

查看试题解析

二、填空题

11. 在平行四边形ABCD中，∠A﹣∠B＝30°，则∠A＝.

查看试题解析
12. 直角三角形两直角边长为5和12，则它斜边上的高为.

查看试题解析
13. 已知方程组 ${\begin{matrix} x + y = 1 \\ 2 x - y = 2 \end{matrix}$ 的解为 ${\begin{matrix} x = 1 \\ y = 0 \end{matrix}$ ，则一次函数y=﹣x+1和y=2x﹣2的图象的交点坐标为．

查看试题解析
14. 将直线y＝2x﹣4的图象向上平移3个单位长度后，所得的直线的解析式是.

查看试题解析
15. 若三角形各边长分别为8cm、10cm、16cm，则以各边中点为顶点的三角形的周长是.

查看试题解析
16. 以正方形ABCD的边AD作等边△ADE，则∠BEC的度数是．

查看试题解析
17. 矩形OABC在平面直角坐标系中的位置如图所示，点B的坐标为（3，4），D是OA的中点，点E在AB上，当△CDE的周长最小时，点E的坐标为.

查看试题解析
18. 如图，正方形ABCD的边长为2，其面积标记为S₁ ，以CD为斜边作等腰直角三角形，以该等腰直角三角形的一条直角边为边向外作正方形，其面积标记为S₂ ， ……按照此规律继续下去，则S₂₀₁₉的值为.

查看试题解析

三、解答题

19. 计算：

(1)、（ $\sqrt{3}$ +1）（ $\sqrt{3}$ ﹣1）+ $\sqrt{2} \times \sqrt{8}$

(2)、（ $\sqrt{48} + \frac{1}{4} \sqrt{6}$ ）÷ $\sqrt{27}$ .

查看试题解析
20. 已知 $y = y_{1} + y_{2}$ ， $y_{1}$ 与 $x$ 成正比例， $y_{2}$ 与 $x - 1$ 成正比例，且 $x = 3$ 时， $y = 4$ ； $x = 1$ 时， $y = 2$ ，求y与x的解析式.

查看试题解析
21. 某住宅小区有一块草坪如图所示.已知AB＝3米，BC＝4米，CD＝12米，DA＝13米，且AB⊥BC，求这块草坪的面积.

查看试题解析
22. 已知：如图ABCD中，点O是AC的中点，过点O画AC的垂线，分别交AD、BC于点E、F.求证：四边形AFCE是菱形.

查看试题解析

23. 小明购买A，B两种商品，每次购买同一种商品的单价相同，具体信息如下表：

次数	购买数量（件 $)$		购买总费用（元 $)$
次数	A	B	购买总费用（元 $)$
第一次	2	1	55
第二次	1	3	65

根据以上信息解答下列问题：

(1)、求A，B两种商品的单价；

(2)、若第三次购买这两种商品共12件，且A种商品的数量不少于B种商品数量的2倍，请设计出最省钱的购买方案，并说明理由.

查看试题解析

24. 如图，在△ABC中，AD⊥BC于D，BD＝AD，DG＝DC.

(1)、求证：△BDG≌△ADC.

(2)、分别取BG、AC的中点E、F，连接DE、DF，则DE与DF有何关系，并说明理由.

(3)、在（2）的条件下，连接EF，若AC＝10，求EF的长.

查看试题解析
25. 如图，已知直线l₁：y＝2x+4与y轴交于A点，与x轴交于点B，经过A点的直线l₂与直线l₁所夹的锐角为45°.

(1)、过点B作CB⊥AB，交l₂于C，求点C的坐标.

(2)、求l₂的函数解析式.

(3)、在直线l₁上存在点M，直线l₂上存在点N，使得点A、O、M、N四点组成的四边形是平行四边形，请直接写出点N的坐标.

查看试题解析
26. 如图，在平面直角坐标系中，正方形OABC的边长为a.直线y＝bx+c交x轴于E，交y轴于F，且a、b、c分别满足﹣（a﹣4）²≥0，c＝ $\sqrt{b - 2} + \sqrt{2 - b}$ +8.

(1)、求直线y＝bx+c的解析式并直接写出正方形OABC的对角线的交点D的坐标；

(2)、直线y＝bx+c沿x轴正方向以每秒移动1个单位长度的速度平移，设平移的时间为t秒，问是否存在t的值，使直线EF平分正方形OABC的面积？若存在，请求出t的值；若不存在，请说明理由；

(3)、点P为正方形OABC的对角线AC上的动点（端点A、C除外），PM⊥PO，交直线AB于M，求 $\frac{P C}{B M}$ 的值.

查看试题解析