浙江省宁波市镇海区2017-2018学年八年级下学期数学期末考试试卷
试卷更新日期:2019-07-05 类型:期末考试
一、单选题
-
1. 要使二次根式 有意义,则x的取值范围是( )A、x<3 B、x≤3 C、x>3 D、x≥32. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
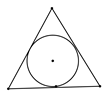 B、
B、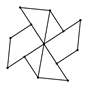 C、
C、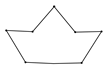 D、
D、 3. 百货商场试销一批新款衬衫,一周内销售情况如表所示,商场经理想要了解哪种型号最畅销,那么他最关注的统计量是( )
3. 百货商场试销一批新款衬衫,一周内销售情况如表所示,商场经理想要了解哪种型号最畅销,那么他最关注的统计量是( )型号(厘米)
38
39
40
41
42
43
数量(件)
23
31
35
48
29
8
A、平均数 B、中位数 C、众数 D、方差4. 用配方法解一元二次方程x2-8x+3=0,此方程可化为( )A、(x-4)2=13 B、(x+4)2=13 C、(x-4)2=19 D、(x+4)2=195. 如图所示,小华从A点出发,沿直线前进10米后左转24°,再沿直线前进10米,又向左转24°,……,照这样走下去,他第一次回到出发地A点时,一共走的路程是( )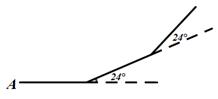 A、140米 B、150米 C、160米 D、240米6. 下列说法中正确的是( )A、有一个角是直角的四边形是矩形 B、两条对角线互相垂直的四边形是菱形 C、两条对角线互相垂直平分的四边形是正方形 D、两条对角线相等的菱形是正方形7. 用反证法证明命题“在三角形中,至多有一个内角是直角”时,应先假设( )A、至少有一个内角是直角 B、至少有两个内角是直角 C、至多有一个内角是直角 D、至多有两个内角是直角8. 某楼盘2016年房价为每平方米15600元,经过两年连续降价后,2018年房价为每平方米12400元。设该楼盘这两年房价每年平均降低率为x,根据题意可列方程为( )A、15600(1-2x)=12400 B、2×15600(1-2x)=12400 C、15600(1-x)2=12400 D、15600(1-x2)=124009. 如图,点A在双曲线 上,点B在双曲线 上,且AB∥y轴,C、D在y轴上,若四边形ABCD为矩形,则它的面积为( )
A、140米 B、150米 C、160米 D、240米6. 下列说法中正确的是( )A、有一个角是直角的四边形是矩形 B、两条对角线互相垂直的四边形是菱形 C、两条对角线互相垂直平分的四边形是正方形 D、两条对角线相等的菱形是正方形7. 用反证法证明命题“在三角形中,至多有一个内角是直角”时,应先假设( )A、至少有一个内角是直角 B、至少有两个内角是直角 C、至多有一个内角是直角 D、至多有两个内角是直角8. 某楼盘2016年房价为每平方米15600元,经过两年连续降价后,2018年房价为每平方米12400元。设该楼盘这两年房价每年平均降低率为x,根据题意可列方程为( )A、15600(1-2x)=12400 B、2×15600(1-2x)=12400 C、15600(1-x)2=12400 D、15600(1-x2)=124009. 如图,点A在双曲线 上,点B在双曲线 上,且AB∥y轴,C、D在y轴上,若四边形ABCD为矩形,则它的面积为( )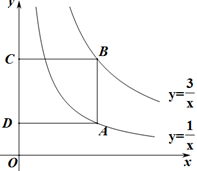 A、1.5 B、1 C、3 D、210. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①a<0;②a-b+c<0;③b2-4ac>0;④2a+b>0,其中正确的是( )
A、1.5 B、1 C、3 D、210. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①a<0;②a-b+c<0;③b2-4ac>0;④2a+b>0,其中正确的是( )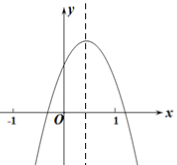 A、①②③④ B、②③④ C、①②③ D、①②④11. 如图,在矩形纸片ABCD中,BC=a,将矩形纸片翻折,使点C恰好落在对角线交点O处,折痕为BE,点E在边CD上,则CE的长为( )
A、①②③④ B、②③④ C、①②③ D、①②④11. 如图,在矩形纸片ABCD中,BC=a,将矩形纸片翻折,使点C恰好落在对角线交点O处,折痕为BE,点E在边CD上,则CE的长为( )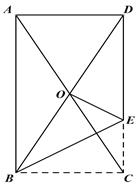 A、 B、 C、 D、12. 一个大矩形按如图方式分割成6个小矩形,且只有标号为②,④的两个小矩形为正方形,若要求出△ABC的面积,则需要知道下列哪个条件? ( )
A、 B、 C、 D、12. 一个大矩形按如图方式分割成6个小矩形,且只有标号为②,④的两个小矩形为正方形,若要求出△ABC的面积,则需要知道下列哪个条件? ( ) A、⑥的面积 B、③的面积 C、⑤的面积 D、⑤的周长
A、⑥的面积 B、③的面积 C、⑤的面积 D、⑤的周长二、填空题
-
13. 的计算结果是.14. 有一组数据如下: 2, 2, 0,1, 4.那么这组数据的平均数为 , 方差为.15. 如果关于x的方程 有实数根,则m的取值范围是.16. 如图,在平面直角坐标系中,直线y= 4x+4与x、y轴分别相交于点A、B,四边形ABCD是正方形,抛物线 过C,D两点,且C为顶点,则a的值为.
 17. 图,在正方向 中, 是对角线 上一点, 的延长线与FG 交于点 ,若 ,则 。 1;
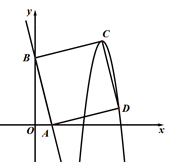
17. 图,在正方向 中, 是对角线 上一点, 的延长线与FG 交于点 ,若 ,则 。 1;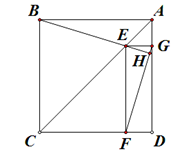 18. 如图,四边形ABCD为菱形,点A在y轴正半轴上,AB∥x轴,点B,C在反比例函数 上,点D在反比例函数 上,那么点D的坐标为.
18. 如图,四边形ABCD为菱形,点A在y轴正半轴上,AB∥x轴,点B,C在反比例函数 上,点D在反比例函数 上,那么点D的坐标为.
三、解答题
-
19. 计算:20. 解方程:(1)、(2)、21. 为了解初二学生参加户外活动的情况,某县教育局对其中500名初二学生每天参加户外活动的时间进行抽样调查,并将调查结果绘制成如下统计图。(参加户外活动的时间分为四种类别:“0.5小时”,“1小时”,“1.5小时”,“2小时”)

请根据图示,回答下列问题:
(1)、求学生每天户外活动时间的平均数,众数和中位数;(2)、该县共有12000名初二学生,请估计该县每天户外活动时间超过1小时的初二学生有多少人?22. 如图,在平面直角坐标系中,直线y1=x+1与双曲线 (k>0)相交于点A、B,已知点A坐标(2,m). (1)、求k的值;(2)、求点B的坐标,并观察图象,写出当 时,x的取值范围.23. 百货商店销售某种冰箱,每台进价2500元.市场调研表明:当销售价为2900元时,平均每天能售出8台;每台售价每降低10元时,平均每天能多售出1台.(销售利润=销售价-进价)(1)、如果设每台冰箱降价x元,那么每台冰箱的销售利润为元,平均每天可销售冰箱台;(用含x的代数式表示)(2)、商店想要使这种冰箱的销售利润平均每天达到5600元,且尽可能地清空冰箱库存,每台冰箱的定价应为多少元?24. 如图,在矩形ABCD中,AB=4,AD=10,点E在AD边上,已知B、E两点关于直线l对称,直线l分别交AD、BC边于点M、N,连接BM、NE.
(1)、求k的值;(2)、求点B的坐标,并观察图象,写出当 时,x的取值范围.23. 百货商店销售某种冰箱,每台进价2500元.市场调研表明:当销售价为2900元时,平均每天能售出8台;每台售价每降低10元时,平均每天能多售出1台.(销售利润=销售价-进价)(1)、如果设每台冰箱降价x元,那么每台冰箱的销售利润为元,平均每天可销售冰箱台;(用含x的代数式表示)(2)、商店想要使这种冰箱的销售利润平均每天达到5600元,且尽可能地清空冰箱库存,每台冰箱的定价应为多少元?24. 如图,在矩形ABCD中,AB=4,AD=10,点E在AD边上,已知B、E两点关于直线l对称,直线l分别交AD、BC边于点M、N,连接BM、NE.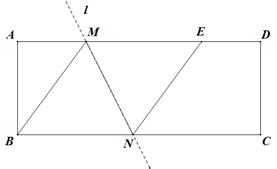 (1)、求证:四边形BMEN是菱形;(2)、若DE=2,求NC的长.25. 如图,抛物线y=﹣x2+bx+c(a≠0)与x轴交于点A(﹣1,0)和B(3,0),与y轴交于点C,点D的横坐标为m(0<m<3),连结DC并延长至E,使得CE=CD,连结BE,BC.
(1)、求证:四边形BMEN是菱形;(2)、若DE=2,求NC的长.25. 如图,抛物线y=﹣x2+bx+c(a≠0)与x轴交于点A(﹣1,0)和B(3,0),与y轴交于点C,点D的横坐标为m(0<m<3),连结DC并延长至E,使得CE=CD,连结BE,BC.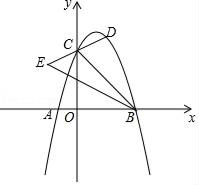 (1)、求抛物线的解析式;(2)、用含m的代数式表示点E的坐标,并求出点E纵坐标的范围;(3)、求△BCE的面积最大值.26. 如图,四边形OABC为矩形,点B坐标为(4,2),A,C分别在x轴,y轴上,点F在第一象限内,OF的长度不变,且反比例函数 经过点F.
(1)、求抛物线的解析式;(2)、用含m的代数式表示点E的坐标,并求出点E纵坐标的范围;(3)、求△BCE的面积最大值.26. 如图,四边形OABC为矩形,点B坐标为(4,2),A,C分别在x轴,y轴上,点F在第一象限内,OF的长度不变,且反比例函数 经过点F.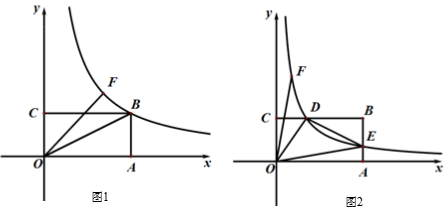 (1)、如图1,当F在直线y = x上时,函数图象过点B,求线段OF的长.(2)、如图2,若OF从(1)中位置绕点O逆时针旋转,反比例函数图象与BC,AB相交,交点分别为D,E,连结OD,DE,OE.
(1)、如图1,当F在直线y = x上时,函数图象过点B,求线段OF的长.(2)、如图2,若OF从(1)中位置绕点O逆时针旋转,反比例函数图象与BC,AB相交,交点分别为D,E,连结OD,DE,OE.①求证:CD=2AE.
②若AE+CD=DE,求k.
③设点F的坐标为(a,b),当△ODE为等腰三角形时,求(a+b)2的值.