云南省曲靖市罗平县2017-2018学年八年级下学期数学期末考试试卷

试卷更新日期：2019-07-05 类型：期末考试

进入出卷网下载

一、单选题

1. 下面式子是二次根式的是（）

A、 $\sqrt{a^{2} + 1}$ B、 $\sqrt[3]{33}$ C、 $\sqrt{- 1}$ D、 $\frac{1}{2}$ a

查看试题解析
2. 下列计算正确的是（）

A、 $\sqrt{2} \cdot \sqrt{3} = \sqrt{6}$ B、 $\sqrt{20} =2 \sqrt{10}$ C、 $\sqrt{4} - \sqrt{2} = \sqrt{2}$ D、 $\sqrt{{(- 3)}^{2}} = - 3$

查看试题解析
3. △ABC的三边为a、b、c，由下列条件不能判断它是直角三角形的是（）

A、∠A: ∠B: ∠C =3∶4∶5 B、∠A=∠B+∠C C、a²=(b+c)(b-c) D、a:b:c =1∶2∶ $\sqrt{3}$

查看试题解析
4. 平面直角坐标系中，将直线l向右平移1个单位长度得到的直线解析式是y=2x+2，则原来的直线解析式是（）

A、y=3x+2 B、y=2x+4 C、y=2x+1 D、y=2x+3

查看试题解析
5. 已知直角三角形的两条边长分别是3和5，那么这个三角形的第三条边的长为（）

A、 $\sqrt{34}$ B、16 C、4或 $\sqrt{34}$ D、4

查看试题解析
6. 如图，四边形ABCD的对角线AC和BD交于点O，则下列不能判断四边形ABCD是平行四边形的条件是（）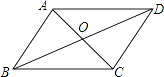

A、OA=OC，AD∥BC B、∠ABC=∠ADC，AD∥BC C、AB=DC，AD=BC D、∠ABD=∠ADB，∠BAO=∠DCO

查看试题解析
7. 某单位组织职工开展植树活动，植树量与人数之间的关系如下表，下列说法不正确的是（）

植树量（棵）

3

4

5

6

7

人数

4

10

8

6

1

A、参加本次植树活动共有29人 B、每人植树量的众数是4 C、每人植树量的中位数是5 D、每人植树量的平均数是5

查看试题解析
8. 如图，E，F，G，H分别是四边形ABCD四条边的中点，要使四边形EFGH为矩形，四边形ABCD应具备的条件是（）

A、对角线互相垂直 B、对角线相等 C、一组对边平行而另一组对边不平行 D、对角线互相平分

查看试题解析

二、填空题

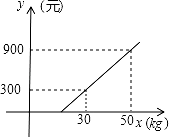
9. 函数y=﹣ $\frac{2}{\sqrt{2 - x}}$ 的自变量x的取值范围是.

查看试题解析
10. 已知y＋2与x－3成正比例，且当x＝0时，y＝1，则当y＝4时，x的值为．

查看试题解析
11. 某航空公司规定，旅客乘机所携带行李的质量x（kg）与其运费y（元）由如图所示的一次函数图象确定，则旅客可携带的免费行李的最大质量为kg.

查看试题解析
12. 如图，以A点为圆心，以相同的长为半径作弧，分别与射线AM，AN交于B，C两点，连接BC，再分别以B，C为圆心，以相同长（大于 $\frac{1}{2}$ BC）为半径作弧，两弧相交于点D，连接AD，BD，CD.若∠MBD=40°，则∠NCD的度数为.

查看试题解析
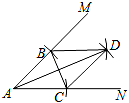13. 如图，正方形ABCD的边长为4，E为BC上的点，BE=1，F为AB的中点，P为AC上一个动点，则PF+PE的最小值为.

查看试题解析
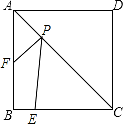14. 如图，在边长为1的菱形ABCD中，∠ABC＝120°连接对角线AC，以AC为边作第二个菱形ACEF，使∠ACE＝120°连接AE，再以AE为边作第三个菱形AEGH，使∠AEG＝120°，…，按此规律所作的第n个菱形的边长是.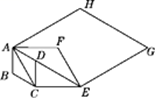

查看试题解析

三、解答题

15. 计算：

(1)、 $\sqrt{48} \div \sqrt{3} - \sqrt{\frac{1}{2}} \times \sqrt{12} + \sqrt{24}$ ；

(2)、 $\sqrt{8} - \frac{2}{3} \times \sqrt{\frac{9}{2}} + {(\sqrt{2} - \sqrt{3})}^{0} - | 1 - \sqrt{2} | - {(\frac{1}{2})}^{- 1}$

查看试题解析
16. 先化简，再求值： $\frac{x + y}{x^{2} - y^{2}} \div (\frac{1}{y} - \frac{1}{x})$ ，其中 $x = \sqrt{3} + \sqrt{2}$ ， $y = \sqrt{3} - \sqrt{2}$ ．

查看试题解析
17. 已知实数a，b，c在数轴上的位置如图所示，化简︱a︱- $\sqrt{{(a + c)}^{2}}$ + $\sqrt{{(c - a)}^{2}}$ - $\sqrt{b^{2}}$ .

查看试题解析
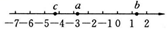18. 如图，甲乙两船同时从A港出发，甲船沿北偏东35°的方向，以每小时12海里的速度向B岛驶去.乙船沿南偏东55°的方向向C岛驶去，2小时后，两船同时到达了目的地.若C、B两岛的距离为30海里，问乙船的航速是多少？

查看试题解析
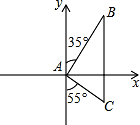19. 如图，在平面直角坐标系中，一次函数y=kx+b的图象与x轴交点为A（﹣3，0），与y轴交点为B，且与正比例函数y= $\frac{4}{3}$ x的图象交于点C（m，4）.

(1)、求m的值及一次函数y=kx+b的表达式；

(2)、观察函数图象，直接写出关于x的不等式 $\frac{4}{3}$ x＜kx+b的解集.

查看试题解析
20. 植树节来临之际，学校准备购进一批树苗，已知2棵甲种树苗和5棵乙种树苗共需113元；3棵甲种树苗和2棵乙种树苗共需87元.

(1)、求一棵甲种树苗和一棵乙种树苗的售价各是多少元；

(2)、学校准备购进这两种树苗共100棵，并且乙种树苗的数量不多于甲种树苗数量的2倍，请设计出最省钱的购买方案，并求出此时的总费用.

查看试题解析
21. 如图所示，△ABC中，D是BC边上一点，E是AD的中点，过点A作BC的平行线交CE的延长线于F，且AF＝BD，连接BF.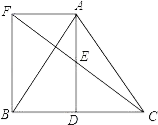

(1)、求证：D是BC的中点；

(2)、若AB＝AC，试判断四边形AFBD的形状，并证明你的结论.

查看试题解析
22.
中国经济的快速发展让众多国家感受到了威胁，随着钓鱼岛事件、南海危机、萨德入韩等一系列事件的发生，国家安全一再受到威胁，所谓“国家兴亡，匹夫有责”，某校积极开展国防知识教育，九年级甲、乙两班分别选5名同学参加“国防知识”比赛，其预赛成绩如图所示：

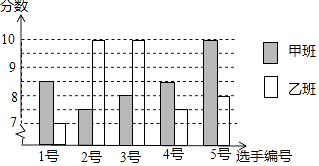(1)、根据上图填写下表：

平均数
中位数
众数
方差
甲班
8.5
8.5
乙班
8.5
10
1.6

(2)、根据上表数据，分别从平均数、中位数、众数、方差的角度分析哪个班的成绩较好．

查看试题解析
23. 如图，在平面直角坐标系中，A（0，8），B（﹣4，0），线段AB的垂直平分线CD分别交AB、OA于点C、D，其中点D的坐标为（0，3）.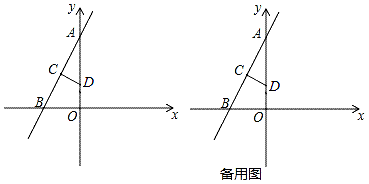

(1)、求直线AB的解析式；

(2)、求线段CD的长；

(3)、点E为y轴上一个动点，当△CDE为等腰三角形时，求E点的坐标.

查看试题解析

植树量（棵）	3	4	5	6	7
人数	4	10	8	6	1

	平均数	中位数	众数	方差
甲班	8.5	8.5
乙班	8.5		10	1.6