云南省昆明市十县区2017-2018学年八年级下学期数学期末考试试卷
试卷更新日期:2019-07-05 类型:期末考试
一、单选题
-
1. 下列根式是最简二次根式的是( )A、 B、 C、 D、2. 下列各组线段能构成直角三角形的一组是( )A、3,4,6 B、5,9,12 C、30,40,50 D、7,12,133. 使二次根式有意义的x的取值范围是( )A、x≠1 B、x≥﹣1 C、x≥1 D、x≠﹣14. 一木杆在离地面5m处析断,木杆顶端落在木杆底端12m处,则木杆析断前高为( )
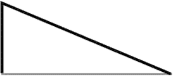 A、18m B、13m C、17m D、12m5. 已知函数y=2x+k﹣1的图象不经过第二象限,则( )A、k<1 B、k>1 C、k≥1 D、k≤16. 某市6月份日平均气温统计如图所示,则在日平均气温这组数据中,众数和中位数分别是( )
A、18m B、13m C、17m D、12m5. 已知函数y=2x+k﹣1的图象不经过第二象限,则( )A、k<1 B、k>1 C、k≥1 D、k≤16. 某市6月份日平均气温统计如图所示,则在日平均气温这组数据中,众数和中位数分别是( )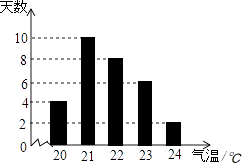 A、21,21 B、21,21.5 C、21,22 D、22,227. 如图,在菱形ABCD中,点A在x轴上,点B的坐标为(8,2),点D的坐标为(0,2),则菱形ABCD面积为( )
A、21,21 B、21,21.5 C、21,22 D、22,227. 如图,在菱形ABCD中,点A在x轴上,点B的坐标为(8,2),点D的坐标为(0,2),则菱形ABCD面积为( )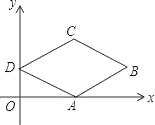 A、8 B、16 C、24 D、328. 一张矩形纸片ABCD,已知AB=3,AD=2,小明按所给图步骤折叠纸片,则线段DG长为( )
A、8 B、16 C、24 D、328. 一张矩形纸片ABCD,已知AB=3,AD=2,小明按所给图步骤折叠纸片,则线段DG长为( )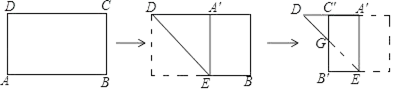 A、2 B、 C、2 D、1
A、2 B、 C、2 D、1二、填空题
-
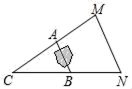
9. = .10. 若点A(2,﹣12)在正比例函数y=kx(k≠0)的图象上,则正比例函数的解析式为.11. 如图,A,B两点被池塘隔开,不能直接测量其距离.于是,小明在岸边选一点C,连接CA,CB,分别延长到点M,N,使AM=AC,BN=BC,测得MN=200m,则A,B间的距离为m.
 12. 学校准备从甲、乙、丙、丁四个科创小组中选出一组代表学校参加青少年科技创新大赛,各组的平时成绩的平均数 (单位:分)及方差s2如表所示:
12. 学校准备从甲、乙、丙、丁四个科创小组中选出一组代表学校参加青少年科技创新大赛,各组的平时成绩的平均数 (单位:分)及方差s2如表所示:甲
乙
丙
丁
7
8
8
7
s2
1
1.2
1
1.8
如果要选出一个成绩较好且状态稳定的组去参赛,那么应选的组是.
13. 如图,在Rt△ABC中,∠ABC=90°,AC=10cm,点D为AC的中点,则BD=cm. 14. 在矩形ABCD中,AB=2,AD=3,点P是BC上的一个动点,连接AP、DP,则AP+DP的最小值为.
14. 在矩形ABCD中,AB=2,AD=3,点P是BC上的一个动点,连接AP、DP,则AP+DP的最小值为.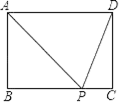 15. 如图,在▱ABCD中,∠D=100°,∠DAB的平分线AE交DC于点E,连接BE.若AE=AB,则∠EBC的度数为.
15. 如图,在▱ABCD中,∠D=100°,∠DAB的平分线AE交DC于点E,连接BE.若AE=AB,则∠EBC的度数为.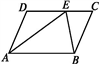
三、解答题
-
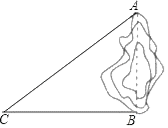
16. 计算:(1)、2 ﹣6 +2(2)、( + ) ﹣3 ÷17. 如图,隔湖有两点A,B,为了测A,B两点间的距离,从与AB方向成直角的BC方向取一点C,若测得CB=150m,∠ACB=30°,求A,B两点间的距离.
 18. 为了了解我县中学生参加“科普知识”竞赛成绩的情况,随机抽查了部分参赛学生的成绩,整理并制作出如下的统计表和统计图,如图所示.请根据图表信息解答下列问题.
18. 为了了解我县中学生参加“科普知识”竞赛成绩的情况,随机抽查了部分参赛学生的成绩,整理并制作出如下的统计表和统计图,如图所示.请根据图表信息解答下列问题.组别
分数段(分)
频数
百分率(%)
A组
60≤x<70
30
10
B组
70≤x<80
90
n
C组
80≤x<90
m
40
D组
90≤x<100
60
20
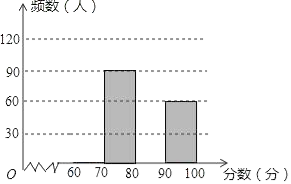
(1)、样本容量a= , 表中m= , n=;(2)、补全频数分布直方图;(3)、若成绩在80分以上(包括80分)为“优”等,请你估计我县参加“科普知识”竞赛的1.5万名学生中成绩是“优”等的约有多少人?
19. 某市规定了每月用水18立方米以内(含18立方米)和用水18立方米以上两种不同的收费标准.该市的用户每月应交水费y(元)是用水量x(立方米)的函数,其图象如图所示. (1)、若每月用水量为18立方米,则应交水费多少元?(2)、求当x>18时,y关于x的函数解析式.若小敏家某月交水费81元,则这个月用水量为多少立方米?20. 如图,矩形ABCD的对角线AC,BD相交于点O,点E,F在BD上,BE=DF.求证:AE=CF.
(1)、若每月用水量为18立方米,则应交水费多少元?(2)、求当x>18时,y关于x的函数解析式.若小敏家某月交水费81元,则这个月用水量为多少立方米?20. 如图,矩形ABCD的对角线AC,BD相交于点O,点E,F在BD上,BE=DF.求证:AE=CF.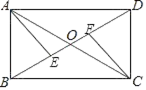 21. 如图,在平行四边形ABCD中,边AB的垂直平分线交AD于点E,交CB的延长线于点F,连接AF,BE.
21. 如图,在平行四边形ABCD中,边AB的垂直平分线交AD于点E,交CB的延长线于点F,连接AF,BE. (1)、求证:△AGE≌△BGF;(2)、试判断四边形AFBE的形状,并说明理由.22. 某蔬菜加工公司先后两批收购蒜苔(tái)共100吨,第一批蒜苔价格为1万元/吨;因蒜苔大量上市,第二批价格跌至0.4万元/吨,这两批蒜苔共用去52万元.(1)、求两批各购进蒜苔多少吨?(2)、公司收购后对蒜苔进行加工,分为粗加工和精加工两种.粗加工每吨利润400元,精加工每吨利润1600元要求精加工数量不大于粗加工数量的三倍.为获得最大利润,精加工数量应为多少吨?最大利润是多少?23. 如图,已知直线l1:y=2x﹣3与直线l2:y=﹣x+3相交于点P,分别与y轴相交于点A、B.
(1)、求证:△AGE≌△BGF;(2)、试判断四边形AFBE的形状,并说明理由.22. 某蔬菜加工公司先后两批收购蒜苔(tái)共100吨,第一批蒜苔价格为1万元/吨;因蒜苔大量上市,第二批价格跌至0.4万元/吨,这两批蒜苔共用去52万元.(1)、求两批各购进蒜苔多少吨?(2)、公司收购后对蒜苔进行加工,分为粗加工和精加工两种.粗加工每吨利润400元,精加工每吨利润1600元要求精加工数量不大于粗加工数量的三倍.为获得最大利润,精加工数量应为多少吨?最大利润是多少?23. 如图,已知直线l1:y=2x﹣3与直线l2:y=﹣x+3相交于点P,分别与y轴相交于点A、B.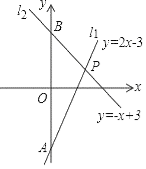 (1)、求点P的坐标;(2)、点M(0,k)为y轴上的一个动点,过点M作y轴的垂线交l1和l2于点N,Q,当NQ=2时,求k的值.
(1)、求点P的坐标;(2)、点M(0,k)为y轴上的一个动点,过点M作y轴的垂线交l1和l2于点N,Q,当NQ=2时,求k的值.