云南省楚雄州2017-2018学年八年级下学期数学期末考试试卷
试卷更新日期:2019-07-05 类型:期末考试
一、单选题
-
1. 下列各组数中是勾股数的为( )A、1、2、3 B、4、5、6 C、3、4、5 D、7、8、92. 汽车开始行驶时,油箱内有油40升,如果每小时耗油5升,则油箱内的余油量Q(升)与行驶时间(t小时)之间的函数关系图象是( )A、
 B、
B、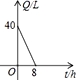 C、
C、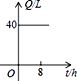 D、
D、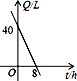 3. 我国在近几年奥运会上所获金牌数(单位:枚)统计如下:
3. 我国在近几年奥运会上所获金牌数(单位:枚)统计如下:届 数
23届
24届
25届
26届
27届
28届
金牌数
15
5
16
16
28
32
则这组数据的众数与中位数分别是( )
A、32、32 B、32、16 C、16、16 D、16、324. 若 ,则下列不等式不成立的是( ).A、 B、 C、 D、5. 如图,△AOB中,∠B=25°,将△AOB绕点O顺时针旋转 60°,得到△A′OB′,边A′B′与边OB交于点C(A′不在 OB上),则∠A′CO的度数为( )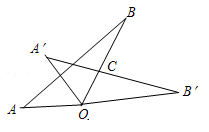 A、85° B、75° C、95° D、105°6. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、
A、85° B、75° C、95° D、105°6. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、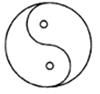 B、
B、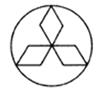 C、
C、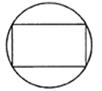 D、
D、 7. 下列多项式中不能用公式分解的是( )A、a2+a+ B、-a2-b2-2ab C、-a2+25 b2 D、-4-b28. 如图,∠1,∠2,∠3,∠4,∠5是五边形ABCDE的外角,且∠1=∠2=∠3=∠4=75°,则∠AED的度数是( )
7. 下列多项式中不能用公式分解的是( )A、a2+a+ B、-a2-b2-2ab C、-a2+25 b2 D、-4-b28. 如图,∠1,∠2,∠3,∠4,∠5是五边形ABCDE的外角,且∠1=∠2=∠3=∠4=75°,则∠AED的度数是( )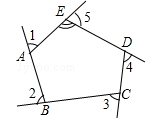 A、120° B、110° C、115° D、100°
A、120° B、110° C、115° D、100°二、填空题
-
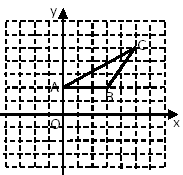
9. 分解因式: .10. 如图,在直角坐标平面内的△ABC中,点A的坐标为(0,2),点C的坐标为(5,5),如果要使△ABD与△ABC全等,且点D坐标在第四象限,那么点D的坐标是;
 11. 如图,△ABC 中,∠C=90°,AC=BC, AD 平分∠BAC 交 BC 于点 D,DE⊥AB,垂足为 E,且 AB=10cm,则△DEB 的周长是cm.
11. 如图,△ABC 中,∠C=90°,AC=BC, AD 平分∠BAC 交 BC 于点 D,DE⊥AB,垂足为 E,且 AB=10cm,则△DEB 的周长是cm. 12. 若m+n=3,则2m2+4mn+2n2-6的值为.13. 如图,E为△ABC中AB边的中点,EF∥AC交BC于点F,若EF=3cm,则AC=.
12. 若m+n=3,则2m2+4mn+2n2-6的值为.13. 如图,E为△ABC中AB边的中点,EF∥AC交BC于点F,若EF=3cm,则AC=.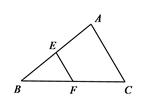 14. 如图,已知函数 和 的图象交于点 ,则不等式 的解集为.
14. 如图,已知函数 和 的图象交于点 ,则不等式 的解集为.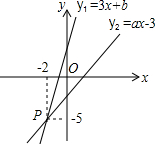
三、解答题
-
15. 化简:16. 解下列不等式组,并把它的解集表示在数轴上:17. 解方程:18. 先化简: ,然后给a选择一个你喜欢的数代入求值。19. 如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题:
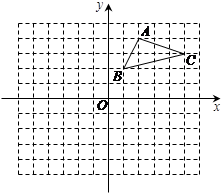
①画出△ABC关于x轴对称的△A1B1C1 , 并写出点A1的坐标;②画出△A1B1C1绕原点O旋转180°后得到的△A2B2C2 , 并写出点A2的坐标.
20. 已知:在平行四边形ABCD中,AM=CN.求证:四边形MBND是平行四边形.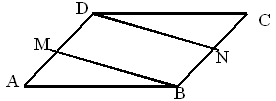 21. 如图,直线l1过点A(0,4),点D(4,0),直线l2: 与x轴交于点C,两直线 , 相交于点B.
21. 如图,直线l1过点A(0,4),点D(4,0),直线l2: 与x轴交于点C,两直线 , 相交于点B. (1)、求直线 的解析式和点B的坐标;(2)、求△ABC的面积.22. 某石化乙烯厂某车间生产甲、乙两种塑料的相关信息如下表,请你解答下列问题:
(1)、求直线 的解析式和点B的坐标;(2)、求△ABC的面积.22. 某石化乙烯厂某车间生产甲、乙两种塑料的相关信息如下表,请你解答下列问题:出厂价
成本价
排污处理费
甲种塑料
2100(元/吨)
800(元/吨)
200(元/吨)
乙种塑料
2400(元/吨)
1100(元/吨)
100(元/吨)
另每月还需支付设备管理、维护费20000元
(1)、设该车间每月生产甲、乙两种塑料各x吨,利润分别为y1元和y2元,分别求出y1和y2与x的函数关系式(注:利润=总收入-总支出);(2)、已知该车间每月生产甲、乙两种塑料均不超过400吨,若某月要生产甲、乙两种塑料共700吨,求该月生产甲、乙塑料各多少吨时,获得的总利润最大?最大利润是多少?23. 将两块全等的三角板如图①摆放,其中∠A1CB1=∠ACB=90°,∠A1=∠A=30°.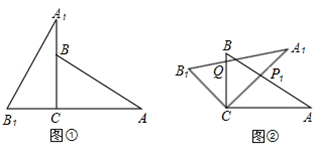 (1)、将图①中的△A1B1C顺时针旋转45°得图②,点P1是A1C与AB的交点,点Q是A1B1与BC的交点,求证:CP1=CQ;(2)、在图②中,若AP1=2,则CQ等于多少?
(1)、将图①中的△A1B1C顺时针旋转45°得图②,点P1是A1C与AB的交点,点Q是A1B1与BC的交点,求证:CP1=CQ;(2)、在图②中,若AP1=2,则CQ等于多少?