广西桂平市2017-2018学年八年级下学期数学期末考试试卷
试卷更新日期：2019-07-05 类型：期末考试
一、单选题
-
1. 点M（1，2）关于y轴对称点的坐标为（ ）A、（﹣1，2） B、（﹣1，﹣2） C、（1，﹣2） D、（2，﹣1）2. 如图所示是一些常用图形的标志，其中是轴对称图形但不是中心对称图形的是（ ）A、
B、
C、
D、
3. 关于函数y=﹣x+3，下列结论正确的是（ ）A、它的图象必经过点（1，1） B、它的图象经过第一、二、三象限 C、它的图象与y轴的交点坐标为（0，3） D、y随x的增大而增大4. 如图，在▱ABCD中，AD=8，点E，F分别是BD，CD的中点，则EF等于（ ）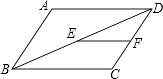
A、2 B、3 C、4 D、55. 如图所示的是一扇高为2m，宽为1.5m的长方形门框，光头强有一些薄木板要通过门框搬进屋内，在不能破坏门框，也不能锯短木板的情况下，能通过门框的木板最大的宽度为（ ）
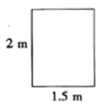A、1.5m B、2m C、2.5m D、3m6. 如图，Rt△ABC中，∠C=90°，AD平分∠BAC，交BC于点D，AB=10，S△ABD=15，则CD的长为（ ）
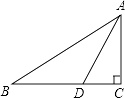A、3 B、4 C、5 D、67. 如图，△ABC中，∠C=90°，AC=3，∠B=30°，点P是BC边上的动点，则AP的长不可能是（ ）
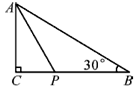A、3.5 B、4.2 C、5.8 D、78. 如图，四边形ABCD是长方形，AB=3，AD=4.已知A（﹣ ，﹣1），则点C的坐标是（ ）
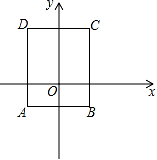A、（﹣3， ） B、（ ，﹣3） C、（3， ） D、（ ，3）9. 如图，四边形ABCD的对角线交于点O，下列哪组条件不能判断四边形ABCD是平行四边形（ ）.
A、OA＝OC，OB＝OD B、∠BAD＝∠BCD，AB∥CD C、AD∥BC，AD＝BC D、AB＝CD，AO＝CO10. 如图，一艘巡逻船由A港沿北偏西60°方向航行5海里至B岛，然后再沿北偏东30°方向航行4海里至C岛，则A、C两港相距（ ）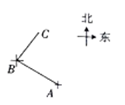
A、4海里 B、 海里 C、3海里 D、5海里11. 如图，购买一种苹果，所付款金额y（元）与购买量x（千克）之间的函数图象由线段OA和射线AB组成，则一次购买5千克这种苹果比分五次购买1千克这种苹果可节省（ ）元.
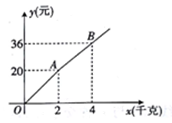A、4 B、5 C、6 D、712.已知：如图，在长方形ABCD中，AB=4，AD=6．延长BC到点E，使CE=2，连接DE，动点P从点B出发，以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动，设点P的运动时间为t秒，当t的值为（ ）秒时．△ABP和△DCE全等．
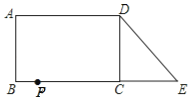A、1 B、1或3 C、1或7 D、3或7二、填空题
-
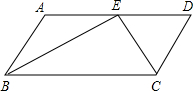
13. 将直线y＝2x+4沿y轴向下平移3个单位，则得到的新直线所对应的函数表达式为.14. 在平面直角坐标系中，点A（x，y）在第三象限，则点B（x，﹣y）在第象限.15. 若三角形三边分别为6，8，10，那么它最长边上的中线长是.16. 如图，在▱ABCD中，BE、CE分别平分∠ABC、∠BCD，E在AD上，BE=12cm，CE=5cm.则▱ABCD的周长为 ， 面积为.
17. 如图，直线AB的解析式为y= x+4，与y轴交于点A，与x轴交于点B，点P为线段AB上的一个动点，作PE⊥y轴于点E，PF⊥x轴于点F，连接EF，则线段EF的最小值为.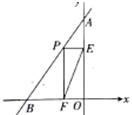
18. 如图，某小区有一块直角三角形绿地，量得直角边AC=4m，BC=3m，考虑到这块绿地周围还有足够多的空余部分，于是打算将这块绿地扩充成等腰三角形，且扩充部分是以AC为一条直角边的直角三角形，则扩充的方案共有种.
三、解答题
-
19. 如图，点E、F在线段BD上，AF⊥BD，CE⊥BD，AD=CB，DE=BF，求证：AF=CE.
20. 如图，直线AB与x轴交于点A（1，0），与y轴交于点B（0，﹣2）．
(1)、求直线AB的解析式；(2)、若直线AB上的点C在第一象限，且S△BOC=2，求点C的坐标．21. 如图，在平面直角坐标系中，网格中每一个小正方形的边长为1个单位长度，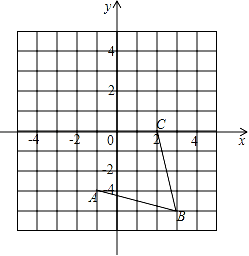
(1)、请在所给的网格内画出以线段AB、BC为边的菱形 ， 并写出点D的坐标.(2)、线段BC的长为 ， 菱形ABCD的面积等于22. 为了庆祝即将到来的2018年国庆节，某校举行了书法比赛，赛后整理了参赛同学的成绩，并制作了如下两幅不完整的统计图表分数段
频数
频率
60≤x＜70
30
0.15
70≤x＜80
m
0.45
80≤x＜90
60
n
90≤x＜100
20
0.1
请根据以上图表提供的信息，解答下列问题：
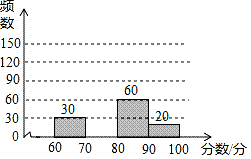(1)、这次共调查了名学生；表中的数m= ， n=.(2)、请补全频数直方图；(3)、若绘制扇形统计图，则分数段60≤x＜70所对应的扇形的圆心角的度数是.23. 某产品每件的成本为10元，在试销阶段每件产品的日销售价x（元）与产品的日销售量y（件）之间的关系如下表：X（元）
15
20
25
…
Y（件）
25
20
15
…
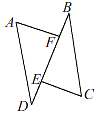
(1)、观察与猜想y与x的函数关系，并说明理由.(2)、求日销售价定为30元时每日的销售利润.24. 如图，点B、C分别在直线y=2x和y=kx上，点A、D是x轴上的两点，且四边形ABCD是正方形.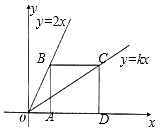
(1)、若正方形ABCD的边长为2，则点B、C的坐标分别为.(2)、若正方形ABCD的边长为a，求k的值.25. 如图，在△ABC中，∠ACB=90°，点D，E分别是边BC，AB上的中点，连接DE并延长至点F，使EF=2DF，连接CE、AF．
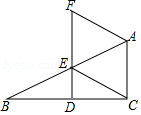(1)、证明：AF=CE；(2)、当∠B=30°时，试判断四边形ACEF的形状并说明理由．26. 如图1，在正方形ABCD中，点E是AB上一点，点F是AD延长线上一点，且DF=BE，连接CE、CF.
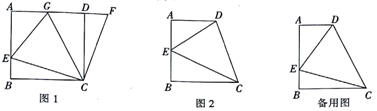(1)、求证：CE=CF.(2)、在图1中，若点G在AD上，且∠GCE=45°，则GE=BE+GD成立吗？为什么？(3)、根据你所学的知识，运用（1）、（2）解答中积累的经验，完成下列各题，如图2，在四边形ABCD中，AD∥BC（BC＞AD），∠B=90°，AB=BC，且∠DCE=45°.①若AE=6，DE=10，求AB的长；
②若AB=BC=9，BE=3，求DE的长.