浙江省丽水市四校联考2018-2019学年高二数学5月阶段性考试试卷
试卷更新日期:2019-07-04 类型:月考试卷
一、单选题
-
1. 抛物线 的焦点坐标为( )A、 B、 C、 D、2. 下列命题正确的是( )A、如果两条直线垂直于同一条直线,那么这两条直线平行 B、如果一条直线垂直于一个平面内的两条直线,那么这条直线垂直于这个平面 C、如果一条直线平行于一个平面内的一条直线,那么这条直线平行于这个平面 D、如果一个平面内的两条相交直线与另一个平面平行,那么这两个平面平行3. “方程 表示一个圆”是“ ”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件4. 函数 在点 处切线方程为( )A、 B、 C、 D、5. 二项式 的展开式中含 项的系数为( )A、60 B、120 C、240 D、4806. 6个人分乘两辆不同的汽车,每辆汽车最多坐4人,则不同的乘车方法种数为( )A、40 B、50 C、60 D、707. 已知函数 , 为 的导函数,则 的图象为( )A、
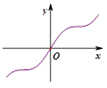 B、
B、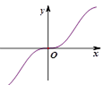 C、
C、 D、
D、 8. 利用数学归纳法证明“ ” 的过程中,由假设“ ”成立,推导“ ”也成立时,左边应增加的项数是( )A、 B、 C、 D、9. 如图,正四面体 中, 是棱 上的动点,设 ( ),记 与 所成角为 , 与 所成角为 ,则( )
8. 利用数学归纳法证明“ ” 的过程中,由假设“ ”成立,推导“ ”也成立时,左边应增加的项数是( )A、 B、 C、 D、9. 如图,正四面体 中, 是棱 上的动点,设 ( ),记 与 所成角为 , 与 所成角为 ,则( )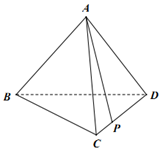 A、 B、 C、当 时, D、当 时,10. 已知 , , 和 为空间中的4个单位向量,且 ,则 不可能等于( )A、3 B、 C、4 D、11. 如图,在三棱柱 中,点 在平面 内运动,使得二面角 的平面角与二面角 的平面角互余,则点 的轨迹是( )
A、 B、 C、当 时, D、当 时,10. 已知 , , 和 为空间中的4个单位向量,且 ,则 不可能等于( )A、3 B、 C、4 D、11. 如图,在三棱柱 中,点 在平面 内运动,使得二面角 的平面角与二面角 的平面角互余,则点 的轨迹是( ) A、一段圆弧 B、椭圆的一部分 C、抛物线 D、双曲线的一支12. 已知椭圆 的左、右焦点分别为 , , 为椭圆上不与左右顶点重合的任意一点, , 分别为 的内心和重心,当 轴时,椭圆的离心率为( )A、 B、 C、 D、
A、一段圆弧 B、椭圆的一部分 C、抛物线 D、双曲线的一支12. 已知椭圆 的左、右焦点分别为 , , 为椭圆上不与左右顶点重合的任意一点, , 分别为 的内心和重心,当 轴时,椭圆的离心率为( )A、 B、 C、 D、二、填空题
-
13. 已知 为虚数单位,复数 ,且复数 满足 ,则 ; .14. 直线 , 的斜率 , 是关于 的方程 的两根,若 ,则 ;若 ,则 .15. 已知某几何体的三视图如图所示,则该几何体的体积为;表面积为 .
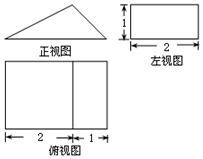 16. 已知双曲线 的虚轴长是实轴长的2倍,则实数 .17. 已知函数 在区间 内不单调,则实数 的取值范围是 .18. 已知 ,则 .19. 在内切圆圆心为 的 中, , , ,在平面 内,过点 作动直线 ,现将 沿动直线 翻折,使翻折后的点 在平面 上的射影 落在直线 上,点 在直线 上的射影为 ,则 的最小值为
16. 已知双曲线 的虚轴长是实轴长的2倍,则实数 .17. 已知函数 在区间 内不单调,则实数 的取值范围是 .18. 已知 ,则 .19. 在内切圆圆心为 的 中, , , ,在平面 内,过点 作动直线 ,现将 沿动直线 翻折,使翻折后的点 在平面 上的射影 落在直线 上,点 在直线 上的射影为 ,则 的最小值为三、解答题

