江苏省宿迁市2019年中考数学试卷
试卷更新日期:2019-07-04 类型:中考真卷
一、单选题
-
1. 2019的相反数是( )A、 B、-2019 C、 D、20192. 下列运算正确的是( )A、 B、 C、 D、3. 一组数据:2、4、4、3、7、7,则这组数据的中位数是( )A、3 B、3.5 C、4 D、74. 一副三角板如图摆放(直角顶点 重合),边 与 交于点 , ,则 等于( )
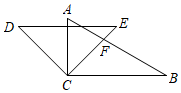 A、 B、 C、 D、5. 一个圆锥的主视图如图所示,根据图中数据,计算这个圆锥的侧面积是( )
A、 B、 C、 D、5. 一个圆锥的主视图如图所示,根据图中数据,计算这个圆锥的侧面积是( ) A、 B、 C、 D、6. 不等式 的非负整数解有( )A、1个 B、2个 C、3个 D、4个7. 如图,正六边形的边长为2,分别以正六边形的六条边为直径向外作半圆,与正六边形的外接圆围成的6个月牙形的面积之和(阴影部分面积)是( )
A、 B、 C、 D、6. 不等式 的非负整数解有( )A、1个 B、2个 C、3个 D、4个7. 如图,正六边形的边长为2,分别以正六边形的六条边为直径向外作半圆,与正六边形的外接圆围成的6个月牙形的面积之和(阴影部分面积)是( ) A、 B、 C、 D、8. 如图,在平面直角坐标系 中,菱形 的顶点 与原点 重合,顶点 落在 轴的正半轴上,对角线 、 交于点 ,点 、 恰好都在反比例函数 的图象上,则 的值为( )
A、 B、 C、 D、8. 如图,在平面直角坐标系 中,菱形 的顶点 与原点 重合,顶点 落在 轴的正半轴上,对角线 、 交于点 ,点 、 恰好都在反比例函数 的图象上,则 的值为( )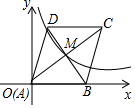 A、 B、 C、2 D、
A、 B、 C、2 D、二、填空题
-
9. 实数4的算术平方根为.10. 分解因式: = .11. 宿迁近年来经济快速发展,2018年 约达到275000000000元.将275000000000用科学记数法表示为.12. 甲、乙两个篮球队队员身高的平均数都为2.07米,方差分别是 、 ,且 ,则队员身高比较整齐的球队是.13. 下面3个天平左盘中“△”“□”分别表示两种质量不同的物体,则第三个天平右盘中砝码的质量为.
 14. 抛掷一枚质地均匀的骰子一次,朝上一面的点数是3的倍数的概率是.15. 直角三角形的两条直角边分别是5和12,则它的内切圆半径为.16. 关于 的分式方程 的解为正数,则 的取值范围是.17. 如图, ,若 的顶点 在射线 上,且 ,点 在射线 上运动,当 是锐角三角形时, 的取值范围是.
14. 抛掷一枚质地均匀的骰子一次,朝上一面的点数是3的倍数的概率是.15. 直角三角形的两条直角边分别是5和12,则它的内切圆半径为.16. 关于 的分式方程 的解为正数,则 的取值范围是.17. 如图, ,若 的顶点 在射线 上,且 ,点 在射线 上运动,当 是锐角三角形时, 的取值范围是. 18. 如图,正方形 的边长为4, 为 上一点,且 , 为 边上的一个动点,连接 ,以 为边向右侧作等边 ,连接 ,则 的最小值为.
18. 如图,正方形 的边长为4, 为 上一点,且 , 为 边上的一个动点,连接 ,以 为边向右侧作等边 ,连接 ,则 的最小值为.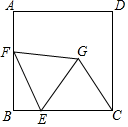
三、解答题
-
19. 计算: .20. 先化简,再求值: ,其中 .21. 如图,一次函数 的图象与反比例函数 的图象相交于点 、 两点.
 (1)、求一次函数表达式;(2)、求 的面积.22. 如图,矩形 中, , ,点 、 分别在 、 上,且 .
(1)、求一次函数表达式;(2)、求 的面积.22. 如图,矩形 中, , ,点 、 分别在 、 上,且 .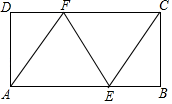 (1)、求证:四边形 是菱形;(2)、求线段 的长.23. 为了解学生的课外阅读情况,七(1)班针对“你最喜爱的课外阅读书目”进行调查(每名学生必须选一类且只能选一类阅读书目),并根据调查结果列出统计表,绘制成扇形统计图.
(1)、求证:四边形 是菱形;(2)、求线段 的长.23. 为了解学生的课外阅读情况,七(1)班针对“你最喜爱的课外阅读书目”进行调查(每名学生必须选一类且只能选一类阅读书目),并根据调查结果列出统计表,绘制成扇形统计图.男、女生所选类别人数统计表
类别
男生(人)
女生(人)
文学类
12
8
史学类
5
科学类
6
5
哲学类
2

根据以上信息解决下列问题
(1)、 , ;(2)、扇形统计图中“科学类”所对应扇形圆心角度数为 ;(3)、从选哲学类的学生中,随机选取两名学生参加学校团委组织的辩论赛,请用树状图或列表法求出所选取的两名学生都是男生的概率.24. 在 中, .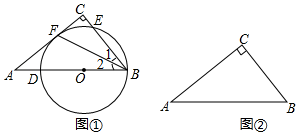 (1)、如图①,点 在斜边 上,以点 为圆心, 长为半径的圆交 于点 ,交 于点 ,与边 相切于点 .求证: ;(2)、在图②中作 ,使它满足以下条件:
(1)、如图①,点 在斜边 上,以点 为圆心, 长为半径的圆交 于点 ,交 于点 ,与边 相切于点 .求证: ;(2)、在图②中作 ,使它满足以下条件:①圆心在边 上;②经过点 ;③与边 相切.
(尺规作图,只保留作图痕迹,不要求写出作法)
25. 宿迁市政府为了方便市民绿色出行,推出了共享单车服务.图①是某品牌共享单车放在水平地面上的实物图,图②是其示意图,其中 、 都与地面l平行,车轮半径为 , , ,坐垫 与点 的距离 为 .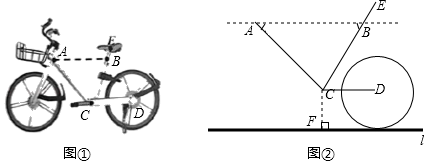 (1)、求坐垫 到地面的距离;(2)、根据经验,当坐垫 到 的距离调整为人体腿长的0.8时,坐骑比较舒适.小明的腿长约为 ,现将坐垫 调整至坐骑舒适高度位置 ,求 的长.
(1)、求坐垫 到地面的距离;(2)、根据经验,当坐垫 到 的距离调整为人体腿长的0.8时,坐骑比较舒适.小明的腿长约为 ,现将坐垫 调整至坐骑舒适高度位置 ,求 的长.(结果精确到 ,参考数据: , , )
26. 超市销售某种儿童玩具,如果每件利润为40元(市场管理部门规定,该种玩具每件利润不能超过60元),每天可售出50件.根据市场调查发现,销售单价每增加2元,每天销售量会减少1件.设销售单价增加 元,每天售出 件.(1)、请写出 与 之间的函数表达式;(2)、当 为多少时,超市每天销售这种玩具可获利润2250元?(3)、设超市每天销售这种玩具可获利 元,当 为多少时 最大,最大值是多少?27. 如图①,在钝角 中, , ,点 为边 中点,点 为边 中点,将 绕点 逆时针方向旋转 度( ).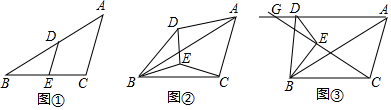 (1)、如图②,当 时,连接 、 .求证: ;(2)、如图③,直线 、 交于点 .在旋转过程中, 的大小是否发生变化?如变化,请说明理由;如不变,请求出这个角的度数;(3)、将 从图①位置绕点 逆时针方向旋转 ,求点 的运动路程.28. 如图,抛物线 交 轴于 、 两点,其中点 坐标为 ,与 轴交于点 .
(1)、如图②,当 时,连接 、 .求证: ;(2)、如图③,直线 、 交于点 .在旋转过程中, 的大小是否发生变化?如变化,请说明理由;如不变,请求出这个角的度数;(3)、将 从图①位置绕点 逆时针方向旋转 ,求点 的运动路程.28. 如图,抛物线 交 轴于 、 两点,其中点 坐标为 ,与 轴交于点 .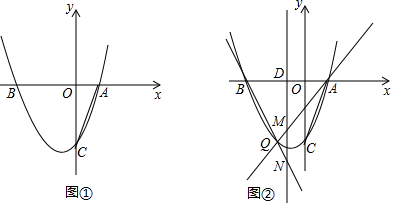 (1)、求抛物线的函数表达式;(2)、如图①,连接 ,点 在抛物线上,且满足 .求点 的坐标;(3)、如图②,点 为 轴下方抛物线上任意一点,点 是抛物线对称轴与 轴的交点,直线 、 分别交抛物线的对称轴于点 、 .请问 是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
(1)、求抛物线的函数表达式;(2)、如图①,连接 ,点 在抛物线上,且满足 .求点 的坐标;(3)、如图②,点 为 轴下方抛物线上任意一点,点 是抛物线对称轴与 轴的交点,直线 、 分别交抛物线的对称轴于点 、 .请问 是否为定值?如果是,请求出这个定值;如果不是,请说明理由.