江苏省兴化市2018-2019学年七年级下学期数学期末考试试卷
试卷更新日期:2019-07-04 类型:期末考试
一、单选题
-
1. 如图,过△ABC的顶点A,作BC边上的高,以下作法正确的是( )A、
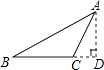 B、
B、 C、
C、 D、
D、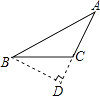 2. 下列多项式相乘,可以用平方差公式直接计算的是( )A、(x+5y)(x-5y) B、(-x+y)(y-x) C、(x+3y)(2x-3y) D、(3x-2y)(2y-3x)3. 下列图形中,由 ,能得到 的是( )A、
2. 下列多项式相乘,可以用平方差公式直接计算的是( )A、(x+5y)(x-5y) B、(-x+y)(y-x) C、(x+3y)(2x-3y) D、(3x-2y)(2y-3x)3. 下列图形中,由 ,能得到 的是( )A、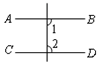 B、
B、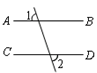 C、
C、 D、
D、 4. 有一根长40mm的金属棒,欲将其截成x根7mm长的小段和y根9mm长的小段,剩余部分作废料处理,若使废料最少,则正整数x,y应分别为( )A、x=1,y=3 B、x=3,y=2 C、x=4,y=1 D、x=2,y=35. 给出下列4个命题:①垂线段最短;②互补的两个角中一定是一个为锐角,另一个为钝角;③同旁内角相等,两直线平行;④同旁内角的两个角的平分线互相垂直.其中真命题的个数为( )A、1 B、2 C、3 D、4
4. 有一根长40mm的金属棒,欲将其截成x根7mm长的小段和y根9mm长的小段,剩余部分作废料处理,若使废料最少,则正整数x,y应分别为( )A、x=1,y=3 B、x=3,y=2 C、x=4,y=1 D、x=2,y=35. 给出下列4个命题:①垂线段最短;②互补的两个角中一定是一个为锐角,另一个为钝角;③同旁内角相等,两直线平行;④同旁内角的两个角的平分线互相垂直.其中真命题的个数为( )A、1 B、2 C、3 D、4二、填空题
-
6. 生物学家发现了一种病毒的长度约为0.00000432毫米,数据0.00000432用科学记数法表示为 .7. 命题“如果a>b,那么ac>bc”的逆命题是.8. 若x2_4x+m是一个完全平方式,则m=.9. 一个多边形的内角和是720°,这个多边形的边数是 .10. 已知am=3,an=2,则am+n的值为.11. 关于x的不等式组 的解集是.12. 若a2-3b=4,则2a2-6b +2019=.13.
如图,AB∥CD , 则∠1+∠3—∠2的度数等于 .
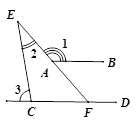 14. 某经销商销售一批电话手表,第一个月以550元/块的价格售出60块,第二个月起降价,以500元/块的价格将这批电话手表全部售出,销售总额超过了5.5万元.这批电话手表至少有块.15. 一副直角三角尺如图①叠放,现将45°的三角尺ADE固定不动,将含30°的三角尺ABC绕顶点A顺时针转动,要求两块三角尺的一组边互相平行.如图②,当∠BAD=15°时,有一组边BC∥DE,请再写出两个符合要求的∠BAD(0°<∠BAD<180°)的度数.
14. 某经销商销售一批电话手表,第一个月以550元/块的价格售出60块,第二个月起降价,以500元/块的价格将这批电话手表全部售出,销售总额超过了5.5万元.这批电话手表至少有块.15. 一副直角三角尺如图①叠放,现将45°的三角尺ADE固定不动,将含30°的三角尺ABC绕顶点A顺时针转动,要求两块三角尺的一组边互相平行.如图②,当∠BAD=15°时,有一组边BC∥DE,请再写出两个符合要求的∠BAD(0°<∠BAD<180°)的度数.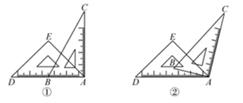
三、解答题
-
16. 计算:(1)、-4+28-(-18)+(-24);(2)、17. 解方程:(1)、x+2 =7-4x;(2)、18.(1)、计算:(-3a3)2·2a3-4a12÷a3;(2)、先化简,再求值:(a+b)2-2a(a-b)+(a+2b)(a-2b),其中a=-1,b=4.19. 因式分解:(1)、 ;(2)、 .20. 解不等式 ,把它的解集在数轴上表示出来,并求出这个不等式的负整数解.21. 如图,在8×8的正方形网格中,每个小正方形的边长都为1个单位长度,△ABC的顶点都在正方形网格的格点上.
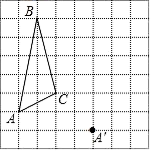 (1)、将△ABC经平移后得到△A′B′C′,点A的对应点是点A′.画出平移后所得的△A′B′C′;(2)、连接AA′、CC′,则四边形AA′C′C的面积为.22.(1)、把下面的证明补充完整:
(1)、将△ABC经平移后得到△A′B′C′,点A的对应点是点A′.画出平移后所得的△A′B′C′;(2)、连接AA′、CC′,则四边形AA′C′C的面积为.22.(1)、把下面的证明补充完整: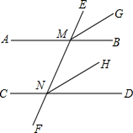
如图,已知直线EF分别交直线AB、CD于点M、N,AB∥CD,MG平分∠EMB,NH平分∠END.求证:MG∥NH
证明:∵AB∥CD(已知)
∴∠EMB=∠END( )
∵MG平分∠EMB,NH平分∠END(已知),
∴∠EMG= ∠EMB,∠ENH= ∠END( ),
∴ (等量代换)
∴MG∥NH( ).
(2)、你在第(1)小题的证明过程中,应用了哪两个互逆的真命题?请直接写出这一对互逆的真命题.23. 有A、B两种型号台灯,若购买2台A型台灯和6台B型台灯共需610元.若购买6台A型台灯和2台B型台灯共需470元.(1)、求A、B两种型号台灯每台分别多少元?(2)、采购员小红想采购A、B两种型号台灯共30台,且总费用不超过2200元,则最多能采购B型台灯多少台?24. 已知:如图,AB平分∠CBD,∠DBC=60°,∠C=∠D.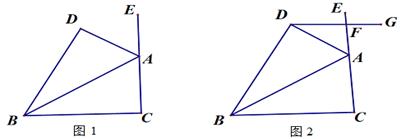 (1)、若AC⊥BC,求∠BAE的度数;(2)、请探究∠DAE与∠C的数量关系,写出你的探究结论,并加以证明;(3)、如图,过点D作DG∥BC交CE于点F,当∠EFG=2∠DAE时,求∠BAD的度数.25. 有一个边长为m+3的正方形,先将这个正方形两邻边长分别增加1和减少1,得到的长方形①的面积为S1.(1)、试探究该正方形的面积S与S1的差是否是一个常数,如果是,求出这个常数;如果不是,说明理由;(2)、再将这个正方形两邻边长分别增加4和减少2,得到的长方形②的面积为S2.
(1)、若AC⊥BC,求∠BAE的度数;(2)、请探究∠DAE与∠C的数量关系,写出你的探究结论,并加以证明;(3)、如图,过点D作DG∥BC交CE于点F,当∠EFG=2∠DAE时,求∠BAD的度数.25. 有一个边长为m+3的正方形,先将这个正方形两邻边长分别增加1和减少1,得到的长方形①的面积为S1.(1)、试探究该正方形的面积S与S1的差是否是一个常数,如果是,求出这个常数;如果不是,说明理由;(2)、再将这个正方形两邻边长分别增加4和减少2,得到的长方形②的面积为S2.①试比较S1 , S2的大小;
②当m为正整数时,若某个图形的面积介于S1 , S2之间(不包括S1 , S2)且面积为整数,这样的整数值有且只有16个,求m的值.