河南省郑州市2018-2019学年七年级下学期数学期末考试试卷
试卷更新日期:2019-07-04 类型:期末考试
一、单选题
-
1. 下面四个手机 APP 图标中,可看作轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列计算正确的是( )A、a2+a2=a4 B、(2a)3=6a3 C、a9÷a3=a3 D、(-2a)2·a3=4a53. 小颖有两根长度为 6cm和 9cm 的木条,桌上有下列长度的几根木条,从中选出一根使三根木条首尾顺次相连,钉成三角形木框,她应该选择长度为( )的木条A、2cm B、3cm C、12cm D、15cm4. 学习整式的乘法时,小明从图1 边长为a 的大正方形中剪掉一个边长为b 的小正方形,将图1 中阴影部分拼成图2 的长方形,比较两个图中阴影部分的面积能够验证的一个等式为( )
2. 下列计算正确的是( )A、a2+a2=a4 B、(2a)3=6a3 C、a9÷a3=a3 D、(-2a)2·a3=4a53. 小颖有两根长度为 6cm和 9cm 的木条,桌上有下列长度的几根木条,从中选出一根使三根木条首尾顺次相连,钉成三角形木框,她应该选择长度为( )的木条A、2cm B、3cm C、12cm D、15cm4. 学习整式的乘法时,小明从图1 边长为a 的大正方形中剪掉一个边长为b 的小正方形,将图1 中阴影部分拼成图2 的长方形,比较两个图中阴影部分的面积能够验证的一个等式为( )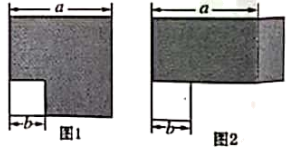 A、a(a+b)=a2+ab B、(a+b)(a-b)=a2-b2 C、(a-b)2=a2-2ab+b2 D、a(a-b)=a2 -ab5. 如图,一把直尺的边缘AB 经过一块三角板 DCB 的直角顶点B,交斜边CD 于点A,直尺的边缘EF 分别交CD、BD 于点E、F,若∠D=60°,∠ABC=20°,则∠1 的度数为( )
A、a(a+b)=a2+ab B、(a+b)(a-b)=a2-b2 C、(a-b)2=a2-2ab+b2 D、a(a-b)=a2 -ab5. 如图,一把直尺的边缘AB 经过一块三角板 DCB 的直角顶点B,交斜边CD 于点A,直尺的边缘EF 分别交CD、BD 于点E、F,若∠D=60°,∠ABC=20°,则∠1 的度数为( ) A、25° B、40° C、50° D、80°6. 某小组作“用频率估计概率的实验时,统计了某一结果出现的频率,绘制了如图所示的折线统计图,则符合这一结果的实验最有可能的是( )
A、25° B、40° C、50° D、80°6. 某小组作“用频率估计概率的实验时,统计了某一结果出现的频率,绘制了如图所示的折线统计图,则符合这一结果的实验最有可能的是( )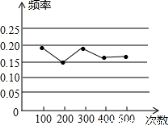 A、掷一个质地均匀的正六面体骰子,向上的面点数是4 B、一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃 C、暗箱中有1个红球和2个黄球,它们只有颜色上的区别,从中任取一球是黄球 D、在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”7. 如图,在Rt△ABC 中,∠C=90°,在AC和AB 上分别截取AE,AD,使 AE=AD分别以点D,E 为圆心,大于立 DE 长为半径作弧,两弧在∠BAC 内交于点F,作射线AF交边BC 于点G,若 CG=4,AB=10,则△ABG 的面积为( )
A、掷一个质地均匀的正六面体骰子,向上的面点数是4 B、一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃 C、暗箱中有1个红球和2个黄球,它们只有颜色上的区别,从中任取一球是黄球 D、在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”7. 如图,在Rt△ABC 中,∠C=90°,在AC和AB 上分别截取AE,AD,使 AE=AD分别以点D,E 为圆心,大于立 DE 长为半径作弧,两弧在∠BAC 内交于点F,作射线AF交边BC 于点G,若 CG=4,AB=10,则△ABG 的面积为( )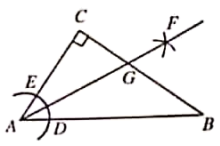 A、12 B、20 C、30 D、408. 等腰三角形一腰的垂直平分线与另一腰所在直线的夹角为 50°,则这个等腰三角形顶角的度数为( )A、40° B、70° C、40°或 70° D、40°或 140°9. 轩轩和凯凯在同一个数学学习小组,在一次数学活动课上,他们各自用一张边长为12cm 的正方形纸片制作了一副七巧板,并合作设计了如图所示的作品请你帮他们计算图中圈出来的三块图形的面积之和为( )
A、12 B、20 C、30 D、408. 等腰三角形一腰的垂直平分线与另一腰所在直线的夹角为 50°,则这个等腰三角形顶角的度数为( )A、40° B、70° C、40°或 70° D、40°或 140°9. 轩轩和凯凯在同一个数学学习小组,在一次数学活动课上,他们各自用一张边长为12cm 的正方形纸片制作了一副七巧板,并合作设计了如图所示的作品请你帮他们计算图中圈出来的三块图形的面积之和为( ) A、12 cm2 B、24 cm2 C、36cm2 D、48 cm210.
A、12 cm2 B、24 cm2 C、36cm2 D、48 cm210.如图,在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG,动点P从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B时停止(不含点A和点B),则△ABP的面积S随着时间t变化的函数图象大致是( )
 A、
A、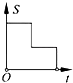 B、
B、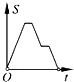 C、
C、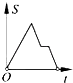 D、
D、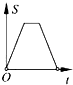
二、填空题
-
11. 近期,被誉为“中国天眼”的 FAST 望远镜首次发现的毫秒脉冲星得到国际认证,新现的脉冲星自转周期为 0.00519秒,将 0.00519 用科学记数法表示应为12. 如图,在 4×4 正方形网格中,已有4 个小正方形被涂黑,现任意选取一个白色的小正方形并涂黑,使整个黑色部分构成一个轴对称图形的概率是
 13. 学习了平行线后,学霸君想出了过已知直线外一点画这条直线的平行线的新方法,她是通过折一张半透明的纸得到的,如图所示,由操作过程可知学霸君画平行线的依据可以是 (把下列所有正确结论的序号都填在横线上)
13. 学习了平行线后,学霸君想出了过已知直线外一点画这条直线的平行线的新方法,她是通过折一张半透明的纸得到的,如图所示,由操作过程可知学霸君画平行线的依据可以是 (把下列所有正确结论的序号都填在横线上)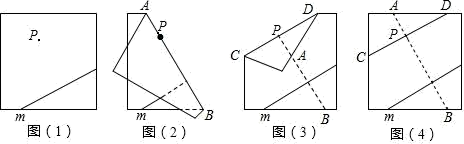
①两直线平行,同位角相等;②同位角相等,两直线平行;③内错角相等,两直线平行;④同旁内角互补,两直线平行.
14. 学习了“设计自己的运算程序”一课后,马老师带领数学兴趣小组同学继续进行探究:任意写一个3 的倍数(非零)的数,先把这个数的每一个数位上的数字都立方,再相加,得到一个新数,然后把这个新数的每一个数位上的数字再立方求和,……重复运算下去,就能得到一个固定的数字 a,我们称它为数字“黑洞”这个数字 a=15. 如图,Rt△ABC中,∠BAC=90°,AB=AC,点D为BC的中点,点E、F分别在边AB和边AC上,且∠EDF=90°,则下列结论一定成立的是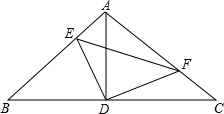
①△ADF≌△BDE②S四边形AEDF= S△ABC③BE+CF=AD④EF=AD
三、解答题
-
16. 如图,已知DE∥BC,∠3=∠B,则∠1+∠2=180°.下面是王宁同学的思考过程,请你在括号内填上理由、依据或内容。
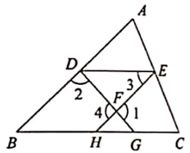
思考过程
因为 DE∥BC(已知)
所以∠3=∠EHC ( )
因为∠3=∠B(已知)
所以∠B=∠EHC ( )
所以 AB∥EH ( )
∠2+ ( )=180°( )
因为∠1=∠4( )
所以∠1+∠2=180°(等量代换)
17. 先化简,再求值[(x+y)2+(x+y)(x-y)]÷(2x),其中 x=-1,y= .18. 如图所示,A、B 两点分别位于一个池塘的两端,小明想用绳子测量A、B 间的距离,但绳子不够长,请你利用三角形全等的相关知识帮他设计一种方案测量出A、B间的距离,写出具体的方案,并解释其中的道理, 19. 暑假将至,丹尼斯大卖场为回馈新老顾客,进行有奖促销活动活动。活动规定:购买500元的商品就可以获得一次转转盘的机会(转盘分为5个区域,分别是特等奖、一等奖、二等奖、三等奖、不获奖),转盘指针停在哪个获奖区域就可以得到该区域相应等级奖品一件(如果指针恰好停在分割线上,那么重转一次,直到指针指向某一区域为止).大卖场工作人员在制作转盘时,将各扇形区域圆心角(不完全)分配如下表:
19. 暑假将至,丹尼斯大卖场为回馈新老顾客,进行有奖促销活动活动。活动规定:购买500元的商品就可以获得一次转转盘的机会(转盘分为5个区域,分别是特等奖、一等奖、二等奖、三等奖、不获奖),转盘指针停在哪个获奖区域就可以得到该区域相应等级奖品一件(如果指针恰好停在分割线上,那么重转一次,直到指针指向某一区域为止).大卖场工作人员在制作转盘时,将各扇形区域圆心角(不完全)分配如下表:奖次
特等奖
一等奖
二等奖
三等奖
不获奖
圆心角
10°
30°
80°
120°
促销公告:凡购买我大卖场商品500元均有可能获得下列奖品:
特等奖:山地越野自行车一辆, 一等奖:双肩背包一个, 二等奖:洗衣液一桶 , 三等奖:抽纸一盒.根据以上信息,解答下列问题
(1)、求不获奖的扇形区域圆心角度数是多少?(2)、求获得双肩背包的概率是多少?(3)、甲顾客购物520元,求他获奖的概率是多少?20. 周六的早上,小颖去郑州图书大厦买书.她先走到早餐店吃早餐,然后又去图书大厦买书,最后又回到家.如图是小颖所用的时间 x(分)和离家的距离 y(千米)之间的示意图,请根据图像解答下列问题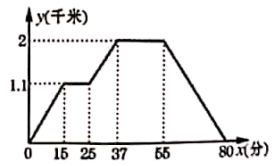 (1)、在上述变化过程中,自变量是 , 因变量是;(2)、早餐店到小颖家的距离是千米,她早餐花了分钟(3)、出发后37分到55分之间小颖在干什么?(4)、小颖从图书大厦回家的过程中,她的平均速度是多少?21. 如图,在正方形网格上有一个三角形 ABC(三个顶点均在格点上)
(1)、在上述变化过程中,自变量是 , 因变量是;(2)、早餐店到小颖家的距离是千米,她早餐花了分钟(3)、出发后37分到55分之间小颖在干什么?(4)、小颖从图书大厦回家的过程中,她的平均速度是多少?21. 如图,在正方形网格上有一个三角形 ABC(三个顶点均在格点上)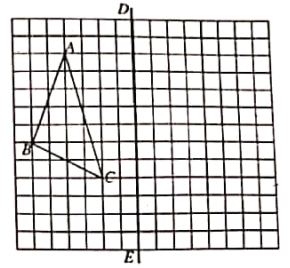 (1)、画出△ABC 关于直线DE对称的△A1B1C1(其中点A 与点 A1对应,点B与点B1对应,点C 与点C1对应)(2)、若每个小正方形的边长都是1,计算△A1B1C1的面积22. 在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)、画出△ABC 关于直线DE对称的△A1B1C1(其中点A 与点 A1对应,点B与点B1对应,点C 与点C1对应)(2)、若每个小正方形的边长都是1,计算△A1B1C1的面积22. 在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.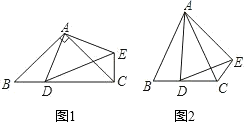 (1)、如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE=度;(2)、设∠BAC=α,∠BCE=β.
(1)、如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE=度;(2)、设∠BAC=α,∠BCE=β.①如图2,当点D在线段BC上移动,则α,β之间有怎样的数量关系?请说明理由;
②当点D在直线BC上移动,则α,β之间有怎样的数量关系?请直接写出你的结论.