江苏省盐城市2019年中考数学试卷
试卷更新日期:2019-07-04 类型:中考真卷
一、选择题(本大题共有8小題,每小题3分,共24分。)
-
1. 如图,数轴上点A表示的数是( )
 A、-1 B、0 C、1 D、22. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
A、-1 B、0 C、1 D、22. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 3. 若 有意义,则x的取值范围是( )A、x≥2 B、x≥-2 C、x>2 D、x>-24. 如图,点D,E分别是△ABC边BA、BC的中点,AC=3,则DE的长为( )
3. 若 有意义,则x的取值范围是( )A、x≥2 B、x≥-2 C、x>2 D、x>-24. 如图,点D,E分别是△ABC边BA、BC的中点,AC=3,则DE的长为( ) A、2 B、 C、3 D、5. 如图是由6个小正方体搭成的物体,该所示物体的主视图是( )
A、2 B、 C、3 D、5. 如图是由6个小正方体搭成的物体,该所示物体的主视图是( )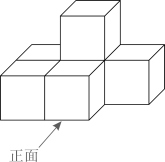 A、
A、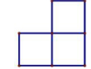 B、
B、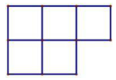 C、
C、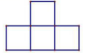 D、
D、 6. 下列运算正确的是( )A、 B、 C、 D、7. 正在建设中的北京大兴国际机场划建设面积约1 400 000平方米的航站极,数据1 400 000用科学记数法应表示为( )A、 B、 C、 D、8. 关于x的一元二次方程 (k为实数)根的情况是( )
6. 下列运算正确的是( )A、 B、 C、 D、7. 正在建设中的北京大兴国际机场划建设面积约1 400 000平方米的航站极,数据1 400 000用科学记数法应表示为( )A、 B、 C、 D、8. 关于x的一元二次方程 (k为实数)根的情况是( )
A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、不能确定二、填空题(本大题共有8小题,每小题3分,共24分。)
-
9. 如图,直线a∥b,∠1=50°,那么∠2=.
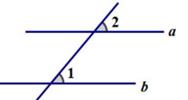 10. 分解因式: .11. 如图,转盘中6个扇形的面积都相等.任意转动转盘1次,当转盘停止转动时,指针落在阴影部分的概率为.
10. 分解因式: .11. 如图,转盘中6个扇形的面积都相等.任意转动转盘1次,当转盘停止转动时,指针落在阴影部分的概率为. 12. 甲、乙两人在100米短跑训练中,某5次的平均成绩相等,甲的方差是0.14 ,乙的方差是0.06 ,这5次短跑训练成绩较稳定的是(填“甲”或“乙”)13. 设 是方程 的两个根,则 .
12. 甲、乙两人在100米短跑训练中,某5次的平均成绩相等,甲的方差是0.14 ,乙的方差是0.06 ,这5次短跑训练成绩较稳定的是(填“甲”或“乙”)13. 设 是方程 的两个根,则 .
14. 如图,点A、B、C、D、E在⊙O上,且弧AB为50°,则∠E+∠C=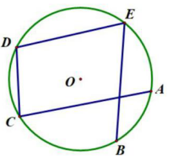 15. 如图,在△ABC中,BC= ,∠C=45°,AB= AC,则AC的长为.
15. 如图,在△ABC中,BC= ,∠C=45°,AB= AC,则AC的长为.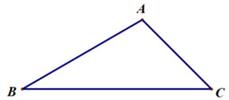 16. 如图,在平面直角坐标系中,一次函数y=2x-1的图像分别交x、y轴于点A、B,将直线AB绕点B按顺时针方向旋转45°,交x轴于点C,则直线BC的函数表达式是.
16. 如图,在平面直角坐标系中,一次函数y=2x-1的图像分别交x、y轴于点A、B,将直线AB绕点B按顺时针方向旋转45°,交x轴于点C,则直线BC的函数表达式是.
三、解答题(本大题共有11小题,共102分。)
-
17. 计算:18. 解不等式组:19. 如图,一次函数y=x+1的图像交y轴于点A,与反比例函数 的图像交于点B(m,2).
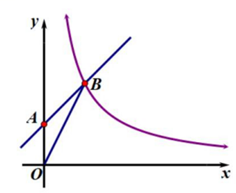 (1)、求反比例函数的表达式:(2)、求△AOB的面积.20. 在一个不透明的布袋中,有2个红球,1个白球,这些球除颜色外都相同(1)、搅匀后从中任意摸出1个球,摸到红球的概率是;(2)、搅匀后先从中任意摸出1个球(不放回),再从余下的球中任意摸出1个球.求两次都摸到红球的概率.(用树状图或表格列出所有等可能出现的结果)21. 如图,AD是△ABC的角平分线
(1)、求反比例函数的表达式:(2)、求△AOB的面积.20. 在一个不透明的布袋中,有2个红球,1个白球,这些球除颜色外都相同(1)、搅匀后从中任意摸出1个球,摸到红球的概率是;(2)、搅匀后先从中任意摸出1个球(不放回),再从余下的球中任意摸出1个球.求两次都摸到红球的概率.(用树状图或表格列出所有等可能出现的结果)21. 如图,AD是△ABC的角平分线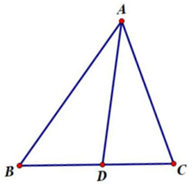 (1)、作线段AD的垂直平分线EF,分别交AB、AC于点E、F;
(1)、作线段AD的垂直平分线EF,分别交AB、AC于点E、F;(用直尺和圆规作图,标明字母,保留作图痕迹,不写作法.)
(2)、连接DE、DF,四边形AEDF是形.(直接写出答案)22. 体育器材室有A、B两种型号的实心球,1只A型球与1只B型球的质量共7千克,3只A型球与1只B型球的质量共13千克.(1)、每只A型球、B型球的质量分别是多少千克?(2)、现有A型球、B型球的质量共17千克,则A型球、B型球各有多少只?23. 某公司其有400名销售人员,为了解该公司销售人员某季度商品销售情况,随机抽取部分销售人员该季度的销售数量,并把所得数据整理后绘制成如下统计图表进行分析.频数分布表 组别 销售数量(件) 人数 频率 A 20≤x<40 3 0.06 B 40≤x<60 7 0.14 C 60≤x<80 13 a D 80≤x<100 m 0.46 E 100≤x<120 4 0.08 合计 b 1 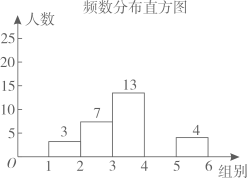
请根据以上信息,解决下列问题:
(1)、频数分布表中,a=、b=:(2)、补全频数分布直方图;(3)、如果该季度销量不低于80件的销售人员将被评为“优秀员工”,试估计该季度被评为“优秀员工”的人数.24. 如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,以CD为直径的⊙O分别交AC、BC于点M、N,过点N作NE⊥AB,垂足为E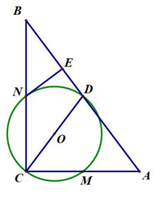 (1)、若⊙O的半径为 ,AC=6,求BN的长;(2)、求证:NE与⊙O相切.25. 如图①是一张矩形纸片,按以下步骤进行操作:
(1)、若⊙O的半径为 ,AC=6,求BN的长;(2)、求证:NE与⊙O相切.25. 如图①是一张矩形纸片,按以下步骤进行操作: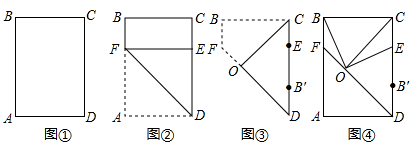
(Ⅰ)将矩形纸片沿DF折叠,使点A落在CD边上点E处,如图②;
(Ⅱ)在第一次折叠的基础上,过点C再次折叠,使得点B落在边CD上点B'处,如图③,两次折痕交于点O;
(Ⅲ)展开纸片,分别连接OB、OE、OC、FD,如图④.
【探究】
(1)、证明:△OBC≌△OED:(2)、若AB=8,设BC为x,OB2为y,求y关于x的关系式.
26.(1)、【生活观察】甲、乙两人买菜,甲习惯买一定质量的菜,乙习惯买一定金额的菜,两人每次买菜的单价相同,例如:菜价3元/千克 质量 金额 甲 1千克 3元 乙 1千克 3元 菜价2元/千克 质量 金额 甲 1千克 元 乙 千克 3元 ①完成上表;
②计算甲两次买菜的均价和乙两次买菜的均价.(均价=总金额÷总质量)
(2)、【数学思考】设甲每次买质量为m千克的菜,乙每次买金额为n元的菜,两次的单价分别是a元/千克、b元/千克,用含有m、n、a、b的式子,分别表示出甲、乙两次买菜的均价 、 .比较 、 的大小,并说明理由.(3)、【知识迁移】某船在相距为s的甲、乙两码头间往返航行一次,在没有水流时,船的速度为v所需时间为:如果水流速度为p时(p<v),船顺水航行速度为(v+p),逆水航行速度为(v-p),所需时间为 请借鉴上面的研究经验,比较 、 的大小,并说明理由.27. 如图所示・二次函数 的图像与一次函数 的图像交于A、B两点,点B在点A的右侧,直线AB分别与x、y轴交于C、D两点,其中k<0. (1)、求A、B两点的横坐标;(2)、若△OAB是以OA为腰的等腰三角形,求k的值;(3)、二次函数图象的对称轴与x轴交于点E,是否存在实数k,使得∠ODC=2∠BEC,若存在,求出k的值;若不存在,说明理由.
(1)、求A、B两点的横坐标;(2)、若△OAB是以OA为腰的等腰三角形,求k的值;(3)、二次函数图象的对称轴与x轴交于点E,是否存在实数k,使得∠ODC=2∠BEC,若存在,求出k的值;若不存在,说明理由.