湖北省黄石市2019年中考数学试卷
试卷更新日期:2019-07-04 类型:中考真卷
一、选择题(本大题共10小题,每小题3分,共30分。)
-
1. 下列四个数: , , , 中,绝对值最大的数是( )A、 B、 C、 D、2. 国际行星命名委员会将紫金山天文台于2007年9月11日发现的编号为171448的小行星命名为“谷超豪星”,则171448用科学记数法可表示为( )A、 B、 C、 D、3. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 如图,该正方体的俯视图是( )
4. 如图,该正方体的俯视图是( )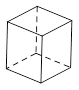 A、
A、 B、
B、 C、
C、 D、
D、 5. 化简 的结果是( )A、 B、 C、 D、6. 若式子 在实数范围内有意义,则 的取值范围是( )A、 且 B、 C、 且 D、7. 如图,在平面直角坐标系中,边长为2的正方形 的边 在 轴上, 边的中点是坐标原点 ,将正方形绕点 按逆时针方向旋转90°后,点 的对应点 的坐标是( )
5. 化简 的结果是( )A、 B、 C、 D、6. 若式子 在实数范围内有意义,则 的取值范围是( )A、 且 B、 C、 且 D、7. 如图,在平面直角坐标系中,边长为2的正方形 的边 在 轴上, 边的中点是坐标原点 ,将正方形绕点 按逆时针方向旋转90°后,点 的对应点 的坐标是( )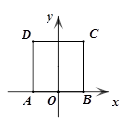 A、(-1,2) B、(1,4) C、(3,2) D、(-1,0)8. 如图,在 中, , 于点 , 和 的角平分线相较于点 , 为边 的中点, ,则 ( )
A、(-1,2) B、(1,4) C、(3,2) D、(-1,0)8. 如图,在 中, , 于点 , 和 的角平分线相较于点 , 为边 的中点, ,则 ( )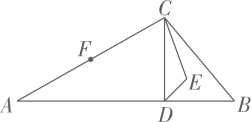 A、125° B、145° C、175° D、190°9. 如图,在平面直角坐标系中,点 在第一象限, 轴于点 ,反比例函数 ( )的图象与线段 相交于点 ,且 是线段 的中点,点 关于直线 的对称点 的坐标为(1, )( ),若 的面积为3,则 的值为( )
A、125° B、145° C、175° D、190°9. 如图,在平面直角坐标系中,点 在第一象限, 轴于点 ,反比例函数 ( )的图象与线段 相交于点 ,且 是线段 的中点,点 关于直线 的对称点 的坐标为(1, )( ),若 的面积为3,则 的值为( )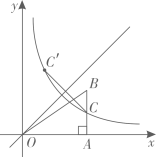 A、 B、1 C、2 D、310. 如图,矩形 中, 与 相交于点 , ,将 沿 折叠,点 的对应点为 ,连接 交 于点 ,且 ,在 边上有一点 ,使得 的值最小,此时 ( )
A、 B、1 C、2 D、310. 如图,矩形 中, 与 相交于点 , ,将 沿 折叠,点 的对应点为 ,连接 交 于点 ,且 ,在 边上有一点 ,使得 的值最小,此时 ( )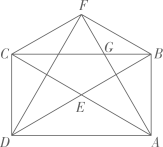 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共6小题,每小题3分,共18分)
-
11. 分解因式:12. 分式方程: 的解为13. 如图,一轮船在 处观测灯塔 位于南偏西30°方向,该轮船沿正南方向以15海里/小时的速度匀速航行2小时后到达 处,再观测灯塔 位于南偏西60°方向,若该轮船继续向南航行至灯塔 最近的位置 处,此时轮船与灯塔之间的距离 为海里(结果保留根号)
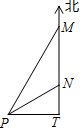
14. 根据下列统计图,回答问题:某超市去年8~11月个月销售总额统计图
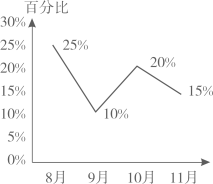
某超市去年8~11月水果销售额占该超市当月销售总额的百分比统计图该超市10月份的水果类销售额11月份的水果类销售额(请从“>” “=” “<”中选一个填空)
15. 如图, 中, =90°, 平分 交 于点 , 是 上一点,经过 、 两点的 分别交 、 于点 、 , , =60°,则劣弧 的长为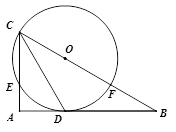 16. 将被3整除余数为1的正整数,按照下列规律排成一个三角形数阵
16. 将被3整除余数为1的正整数,按照下列规律排成一个三角形数阵则第20行第19个数是
三、解答题(本大题共9小题,共72分.)
-
17.18. 先化简,再求值: ,其中 .19. 若点 的坐标为( , ),其中 满足不等式组 ,
求点 所在的象限.
20. 已知关于 的一元二次方程 有实数根.(1)、求 的取值范围.(2)、若该方程的两个实数根为 、 ,且 ,求 的值.21. 如图,在 中, , 为边 上的点,且 , 为线段 的中点,过点 作 ,过点 作 ,且 、 相交于点 .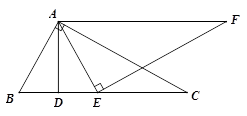 (1)、求证:
(1)、求证:
(2)、求证:
22. 将正面分别写着数字1,2,3的三张卡片(注:这三张卡片的形状、大小、质地、颜色等其它方面完全相同,若背面朝上放在桌面上,这三张卡片看上去无任何差别)洗匀后,背面朝上方在桌面上,甲从中随机抽取一张卡片,记该卡片上的数字为 ,然后放回洗匀,背面朝上方在桌面上,再由乙从中随机抽取一张卡片,记该卡片上的数字为 ,组成一数对( ).(1)、请写出( ).所有可能出现的结果;(2)、甲、乙两人玩游戏,规则如下:按上述要求,两人各抽一次卡片,卡片上述数字和为奇数则甲赢,数字之和为偶数则乙赢,你认为这个游戏公平吗?请说明理由.
23. “今有善行者行一百步,不善行者行六十步”(出自《九章算术》)意思是:同样时间段内,走路快的人能走100步,走路慢的人只能走60步,假定两者步长相等,据此回答以下问题:(1)、今不善行者先行一百步,善行者追之,不善行者再行六百步,问孰至于前,两者几何步隔之?即:走路慢的人先走100步,走路快的人开始追赶,当走路慢的人再走600步时,请问谁在前面,两人相隔多少步?(2)、今不善行者先行两百步,善行者追之,问几何步及之?即:走路慢的人先走200步,请问走路快的人走多少步才能追上走路慢的人?