湖北省(江汉油田、潜江、天门、仙桃)市2019年中考数学试卷
试卷更新日期:2019-07-04 类型:中考真卷
一、选择题(本大题共10个小题,每小题3分,满分30分.)
-
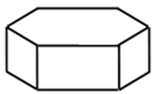
1. 下列各数中,是无理数的是( )A、3.1415 B、 C、 D、2. 如图所示的正六棱柱的主视图是( )
 A、
A、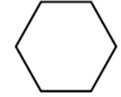 B、
B、 C、
C、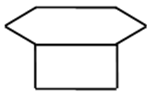 D、
D、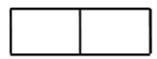 3. 据海关统计,今年第一季度我国外贸进出口总额是70100亿元人民币,比去年同期增长了3.7%,数70100亿用科学记数法表示为( )A、7.01×104 B、7.01×1011 C、7.01×1012 D、7.01×10134. 下列说法正确的是( )A、了解我市市民知晓“礼让行人”交通新规的情况,适合全面调查 B、甲、乙两人跳远成绩的方差分别为S2甲=3,S2乙=4,说明乙的跳远成绩比甲稳定 C、一组数据2,2,3,4的众数是2,中位数是2.5 D、可能性是1%的事件在一次试验中一定不会发生5. 如图,CD∥AB , 点O在AB上,OE平分∠BOD , OF⊥OE , ∠D=110°,则∠AOF的度数是( )
3. 据海关统计,今年第一季度我国外贸进出口总额是70100亿元人民币,比去年同期增长了3.7%,数70100亿用科学记数法表示为( )A、7.01×104 B、7.01×1011 C、7.01×1012 D、7.01×10134. 下列说法正确的是( )A、了解我市市民知晓“礼让行人”交通新规的情况,适合全面调查 B、甲、乙两人跳远成绩的方差分别为S2甲=3,S2乙=4,说明乙的跳远成绩比甲稳定 C、一组数据2,2,3,4的众数是2,中位数是2.5 D、可能性是1%的事件在一次试验中一定不会发生5. 如图,CD∥AB , 点O在AB上,OE平分∠BOD , OF⊥OE , ∠D=110°,则∠AOF的度数是( )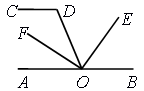 A、20° B、25° C、30° D、35°6. 不等式组 的解集在数轴上表示正确的是( )A、
A、20° B、25° C、30° D、35°6. 不等式组 的解集在数轴上表示正确的是( )A、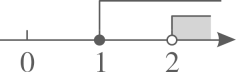 B、
B、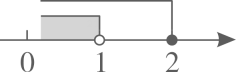 C、
C、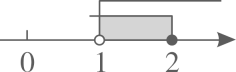 D、
D、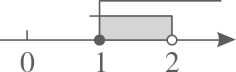 7. 若方程x2-2x-4=0的两个实数根为 , ,则 的值为( )
7. 若方程x2-2x-4=0的两个实数根为 , ,则 的值为( )
A、12 B、10 C、4 D、-4.8. 把一根9m长的钢管截成1m长和2m长两种规格均有的短钢管,且没有余料,设某种截法中1m长的钢管有a根,则a的值可能有( )A、3种 B、4种 C、5种 D、9种9. 反比例函数 ,下列说法不正确的是( )A、图象经过点(1,-3) B、图象位于第二、四象限 C、图象关于直线y=x对称 D、y随x的增大而增大10. 如图,AB为⊙O的直径,BC为⊙O的切线,弦AD∥OC , 直线CD交BA的延长线于点E , 连接BD . 下列结论:①CD是⊙O的切线;②CO⊥DB;③△EDA∽△EBD;④ED·BC=BO·BE . 其中正确结论的个数有( )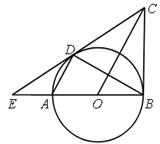 A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题(本大题共6个小题,每小题3分,满分18分.)
-
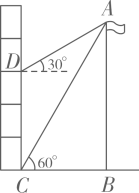
11. 分解因式:x4-4x2= .12. 75°的圆心角所对的弧长是 cm,则此弧所在圆的半径是cm.13. 矩形的周长等于40,则此矩形面积的最大值是 .14. 一个不透明的口袋中有四个完全相同的小球,其上分别标有数字1,2,4,8.随机摸取一个小球后不放回,再随机摸取一个小球,则两次取出的小球上数字之积等于8的概率是 .15. 如图,为测量旗杆AB的高度,在教学楼一楼点C处测得旗杆顶部的仰角为60°,在四楼点D处测得旗杆顶部的仰角为30°,点C与点B在同一水平线上.已知CD=9.6m,则旗杆AB的高度为m.
 16. 如图,在平面直角坐标系中,四边形OA1B1C1 , A1 A2B2C2 , A2A3B3C3 , …都是菱形,点A1 , A2 , A3 , …都在x轴上,点C1 , C2 , C3 , …都在直线 上,且∠C1OA1 =∠C2A1 A2=∠C3A2A3=…=60°,OA1=1,则点C6的坐标是 .
16. 如图,在平面直角坐标系中,四边形OA1B1C1 , A1 A2B2C2 , A2A3B3C3 , …都是菱形,点A1 , A2 , A3 , …都在x轴上,点C1 , C2 , C3 , …都在直线 上,且∠C1OA1 =∠C2A1 A2=∠C3A2A3=…=60°,OA1=1,则点C6的坐标是 .
三、解答题(本大题共8个小题,满分72分.
-
17.(1)、计算: ;(2)、解分式方程: .18. 请仅用无刻度的直尺完成下列画图,不写画法,保留画图痕迹.
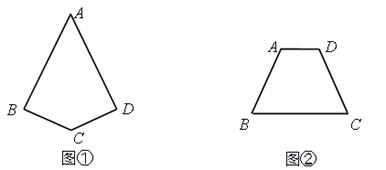
Ⅰ.如图①,四边形ABCD中,AB=AD , ∠B=∠D , 画出四边形ABCD的对称轴m;
Ⅱ.如图②,四边形ABCD中,AD∥BC , ∠A=∠D , 画出BC边的垂直平分线n .
19. 为了解某地七年级学生身高情况,随机抽取部分学生,测得他们的身高(单位:cm),并绘制了如下两幅不完整的统计图,请结合图中提供的信息,解答下列问题.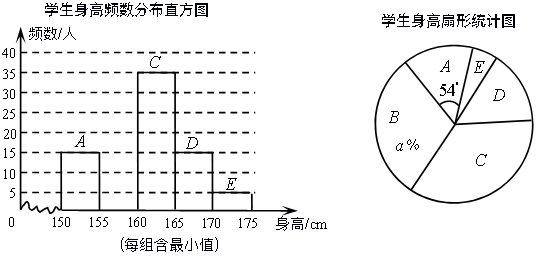 (1)、填空:样本容量为 , a=;(2)、把频数分布直方图补充完整;(3)、若从该地随机抽取1名学生,估计这名学生身高低于160cm的概率.20. 某农贸公司销售一批玉米种子,若一次购买不超过5千克,则种子价格为20元/千克,若一次购买超过5千克,则超过5千克部分的种子价格打8折.设一次购买量为x千克,付款金额为y元.(1)、求y关于x的函数解析式;(2)、某农户一次购买玉米种子30千克,需付款多少元?21. 如图,E , F分别是正方形ABCD的边CB , DC延长线上的点,且BE=CF , 过点E作EG∥BF , 交正方形外角的平分线CG于点G , 连接GF . 求证:
(1)、填空:样本容量为 , a=;(2)、把频数分布直方图补充完整;(3)、若从该地随机抽取1名学生,估计这名学生身高低于160cm的概率.20. 某农贸公司销售一批玉米种子,若一次购买不超过5千克,则种子价格为20元/千克,若一次购买超过5千克,则超过5千克部分的种子价格打8折.设一次购买量为x千克,付款金额为y元.(1)、求y关于x的函数解析式;(2)、某农户一次购买玉米种子30千克,需付款多少元?21. 如图,E , F分别是正方形ABCD的边CB , DC延长线上的点,且BE=CF , 过点E作EG∥BF , 交正方形外角的平分线CG于点G , 连接GF . 求证: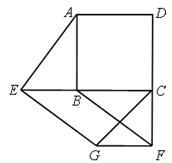 (1)、AE⊥BF;(2)、四边形BEGF是平行四边形.22. 如图,在平面直角坐标系中,四边形OABC的顶点坐标分别为O(0,0),A(12,0),B(8,6),C(0,6).动点P从点O出发,以每秒3个单位长度的速度沿边OA向终点A运动;动点Q从点B同时出发,以每秒2个单位长度的速度沿边BC向终点C运动.设运动的时间为t秒,PQ2=y .
(1)、AE⊥BF;(2)、四边形BEGF是平行四边形.22. 如图,在平面直角坐标系中,四边形OABC的顶点坐标分别为O(0,0),A(12,0),B(8,6),C(0,6).动点P从点O出发,以每秒3个单位长度的速度沿边OA向终点A运动;动点Q从点B同时出发,以每秒2个单位长度的速度沿边BC向终点C运动.设运动的时间为t秒,PQ2=y .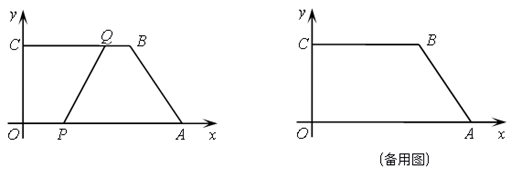 (1)、直接写出y关于t的函数解析式及t的取值范围:;(2)、当PQ= 时,求t的值;(3)、连接OB交PQ于点D , 若双曲线 (k≠0)经过点D , 问k的值是否变化?若不变化,请求出k的值;若变化,请说明理由.23. 已知△ABC内接于⊙O , ∠BAC的平分线交⊙O于点D , 连接DB , DC .
(1)、直接写出y关于t的函数解析式及t的取值范围:;(2)、当PQ= 时,求t的值;(3)、连接OB交PQ于点D , 若双曲线 (k≠0)经过点D , 问k的值是否变化?若不变化,请求出k的值;若变化,请说明理由.23. 已知△ABC内接于⊙O , ∠BAC的平分线交⊙O于点D , 连接DB , DC .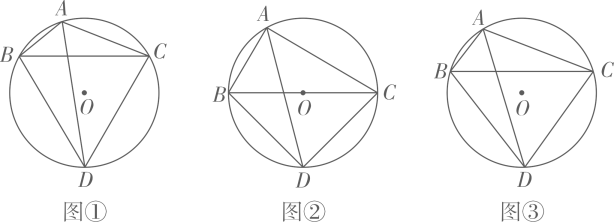 (1)、如图①,当∠BAC =120°时,请直接写出线段AB , AC , AD之间满足的等量关系式:;(2)、如图②,当∠BAC =90°时,试探究线段AB , AC , AD之间满足的等量关系,并证明你的结论;(3)、如图③,若BC=5,BD=4,求 的值.24. 在平面直角坐标系中,已知抛物线C:y=ax2+2x-1(a≠0)和直线l:y=kx+b , 点A(-3,-3),B(1,-1)均在直线l上.(1)、若抛物线C与直线l有交点,求a的取值范围;(2)、当a=-1,二次函数y=ax2+2x-1的自变量x满足m≤x≤m+2时,函数y的最大值为-4, 求m的值;(3)、若抛物线C与线段AB有两个不同的交点,请直接写出a的取值范围.
(1)、如图①,当∠BAC =120°时,请直接写出线段AB , AC , AD之间满足的等量关系式:;(2)、如图②,当∠BAC =90°时,试探究线段AB , AC , AD之间满足的等量关系,并证明你的结论;(3)、如图③,若BC=5,BD=4,求 的值.24. 在平面直角坐标系中,已知抛物线C:y=ax2+2x-1(a≠0)和直线l:y=kx+b , 点A(-3,-3),B(1,-1)均在直线l上.(1)、若抛物线C与直线l有交点,求a的取值范围;(2)、当a=-1,二次函数y=ax2+2x-1的自变量x满足m≤x≤m+2时,函数y的最大值为-4, 求m的值;(3)、若抛物线C与线段AB有两个不同的交点,请直接写出a的取值范围.