湖北省黄冈市2019年中考数学试卷

试卷更新日期：2019-07-04 类型：中考真卷

进入出卷网下载

一、选择题（本题共8小题，每小题3分，共24分。）

1. $- 3$ 的绝对值是（）

A、 $- 3$ B、 $- \frac{1}{3}$ C、 $3$ D、 $\pm 3$

查看试题解析
2. 为纪念中华人民共和国成立70周年，我市各中小学积极开展了以“祖国在我心中”为主题的各类教育活动，全市约有550000名中小学生参加，其中数据550000用科学记数法表示为（）

A、 $5.5 \times 10^{6}$ B、 $5.5 \times 10^{5}$ C、 $55 \times 10^{4}$ D、 $0.55 \times 10^{6}$

查看试题解析
3. 下列运算正确的是（）

A、 $a \cdot a^{2} = a^{2}$ B、 $5 a \cdot 5 a b = 5 a b$ C、 $a^{5} \div a^{3} = a^{2}$ D、 $2 a + 3 b = 5 a b$

查看试题解析
4. 若x₁·x₂是一元一次方程 $x^{2} - 4 x - 5 = 0$ 的两根，则x₁·x₂的值为（）

A、-5 B、5 C、-4 D、4

查看试题解析
5. 已知点A的坐标为（2，1），将点A向下平移4个单位长度，得到的点A’的坐标是（）

A、（6，1） B、（-2，1） C、（2，5） D、（2，-3）

查看试题解析
6. 如图，是有棱长都相等的四个小正方体组成的几何体。该几何体的左视图是（）

A、 B、 C、 D、

查看试题解析
7. 如图，一条公路的转弯处是一段圆弧（AB），点O是这段弧所在圆的圆心，AB=40m，点C是AB的中点，且CD=10m，则这段弯路所在圆的半径为（）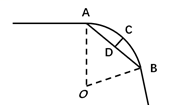

A、25m B、24m C、30m D、60m

查看试题解析
8. 已知林茂的家、体育场、文具店在同一直线上，图中的信息反映的过程是林茂从家跑步去体育场，在体育场锻炼了一阵后又走到文具店买笔，然后再走回家，图中 $x$ 表示时间， $y$ 表示林茂离家的距离。依据图中的信息，下列说法错误的是（）

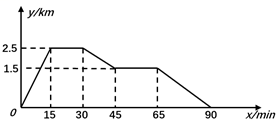A、体育场离林茂家2.5km B、体育场离文具店1km C、林茂从体育场出发到文具店的平均速度是50m/min D、林茂从文具店回家的平均速度是60m/min

查看试题解析

二、填空题（本题共8小题，每小题3分，共24分）

9. 计算 ${(\sqrt{3})}^{2} + 1$ 的结果是.

查看试题解析
10. $- \frac{1}{2} x^{2} y$ 是次单项式.

查看试题解析
11. 分解因式 $3 x^{2} - 27 y^{2} =$ .

查看试题解析
12. 一组数据1，7，8，5，4的中位数是 $a$ ，则 $a$ 的值是 .

查看试题解析
13. 如图，直线AB∥CD，直线EC分别与AB，CD相交于点A、点C，AD平分∠BAC，已知∠ACD=80°，则∠DAC的度数为 .

查看试题解析
14. 用一个圆心角为120°，半径为6的扇形做一个圆锥的侧面，则这个圆锥的底面圆的面积为 .

查看试题解析
15. 如图，一直线经过原点O ，且与反比例函数 $y = \frac{k}{x} （ k > 0 ）$ 相交于点A、点B，过点A作AC⊥y轴，垂足为C，连接BC。若 $△$ ABC面积为8，则 $k =$ .

查看试题解析
16. 如图，AC，BD在AB的同侧，AC=2，BD=8，AB=8，点M为AB的中点，若∠CMD=120°，则CD的最大值是.

查看试题解析

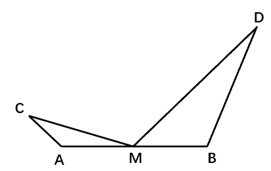
三、解答题（本题共9题，满分72分）

17. 先化简，再求值.
$(\frac{5 a + 3 b}{a^{2} - b^{2}} + \frac{8 b}{b^{2} - a^{2}}) \div \frac{1}{a^{2} b + a b^{2}}$ 其中 $a = \sqrt{2} ， b = 1.$

查看试题解析
18. 解不等式组 ${\begin{matrix} \frac{5 x - 1}{6} + 2 > \frac{x + 5}{4} \\ 2 x + 5 < 3 (5 - x) \end{matrix}$ .

查看试题解析
19. 如图，ABCD是正方形，E是CD边上任意一点，连接AE，作BF⊥AE，DG垂直AE，垂足分别为F，G.求证：BF-DG=FG.

查看试题解析
20. 为了对学生进行革命传统教育，红旗中学开展了“清明节祭扫”活动。全校学生从学校同时出发，步行4000米到达烈士纪念馆。学校要求九（1）班提前到达目的地，做好活动的准备工作。行走过程中，九（1）班步行的平均速度是其他班的1.25倍，结果比其他班提前10分钟到达。分别求九（1）班、其他班步行的平均速度.

查看试题解析
21. 某校开发了“书画、器乐、戏曲、棋类”四大类兴趣课程。为了解全校学生对每类课程的选择情况，随机抽取了若干名学生进行调查（每人必选且只能选一类），先将调查结果绘制成如下两幅不完整的统计图：

(1)、本次随机调查了多少名学生？

(2)、补全条形统计图中“书画”、“戏曲”的空缺部分；

(3)、若该校共有1200名学生，请估计全校学生选择“戏曲”类的人数；

(4)、学校从这四类课程中随机抽取两类参加“全市青少年才艺展示活动”，用树形图或列表法求处恰好抽到“器乐”和“戏曲”类的概率（书画、器乐、戏曲、棋类可分别用字幕A，B，C，D表示）

查看试题解析
22. 如图，两座建筑物的水平距离BC为40m，从A点测得D点的俯角α为45°，测得C点的俯角β为60°。求这两座建筑物AB，CD的高度。（结果保留小数点后一位 $\sqrt{2} \approx 1.414 ， \sqrt{3} \approx 1.732.$ ）

查看试题解析
23. 如图，在Rt $△ ABC$ 中，∠ACB=90°，以AC为直径的⊙0交AB于点D，过点D作⊙0的切线交BC于点E，连接OE.

(1)、求证： $△ DBE$ 是等腰三角形；

(2)、求证： $△ COE ~ △ CAB$

查看试题解析
24. 某县积极响应市政府加大产业扶贫力度的号召，决定成立草莓产销合作社，负责扶贫对象户种植草莓的技术指导和统一销售，所获利润年底分红。经市场调研发现，草莓销售单价y（万元）与产量x（吨）之间的关系如图所示（0≤x≤100），已知草莓的产销投入总成本p（万元）与产量x（吨）之间满足p=x+1.

(1)、直接写出草莓销售单价y（万元）与产量x（吨）之间的函数关系式；

(2)、求该合作社所获利润w（万元）与产量x（吨）之间的函数关系式；

(3)、为提高农民种植草莓的积极性，合作社决定按0.3万元/吨的标准奖励扶贫对象种植户，为确保合作社所获利润w’（万元）不低于55万元，产量至少要达到多少吨？

查看试题解析
25. 如图1在平面直角坐标系xOy中，已知A（-2，2），B（-2，0），C（0，2），D（2，0）四点，动点M以每秒 $\sqrt{2}$ 个单位长度的速度沿B→C→D运动（M不与点B、点D重合），设运动时间为t（秒）.

(1)、求经过A、C、D三点的抛物线的解析式；

(2)、点P在（1）中的抛物线上，当M为BC的中点时，若 $△ PAM ≅ △ PBM$ ，求点P的坐标；

(3)、当M在CD上运动时，如图2，过点M作MF⊥x轴，垂足为F，ME垂直AB，垂足为E.设矩形MEBF与 $△ BCD$ 重叠部分的面积为S，求S与t的函数关系式，并求出S的最大值；

(4)、点Q为x轴上一点，直线AQ与直线BC交于点H，与y轴交于点K.是否存在点Q，使得 $△ HOK$ 为等腰三角形？若存在，直接写出符合条件的所有Q点的坐标；若不存在，请说明理由.

查看试题解析