浙江省杭州市余杭区2018-2019年八年级下学期数学期末考试试卷
试卷更新日期:2019-07-04 类型:期末考试
一、仔细选一选(本题有10个小题,每小题3分,共30分.)
-
1. 二次根式 中,字母a的取值范围是( )A、a> B、a< C、a≥ D、a≤2. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、线段 B、直角三角形 C、等边二角形 D、平行四边形3. 已知关于x的一元二次方程x2+ax-a=0的一个根是-2,则a的值为( )A、4 B、-4 C、 D、4. 已知点(2,-1)在反比例函数y= (k≠0)的图象上,则这个函数图象一定经过点( )A、(-2,-1) B、( , ) C、(6, ) D、( ,1)5. 某班30名学生的身高情况如下表:
身高(m)
1.45
1.48
1.50
1.53
1.56
1.60
人数
x
y
6
8
5
4
关于身高的统计量中,不随x、y的变化而变化的有( )
A、众数,中位数 B、中位数,方差 C、平均数,方差 D、平均数,众数6. 在 ABCD中,E,F是对角线BD上的两点(不与点B,D重合).下列条件中,无法判断四边形AECF一定为平行四边形的是( )A、AE∥CF B、AE=CF C、BE=DF D、∠BAE=∠DCF7. 关于x的一元二次方程ax2+bx=2(a,b是常数,且a≠0),( )A、若a>0,则方程可能有两个相等的实数根 B、若a>0,则方程可能没有实数根 C、若a<0,则方程可能有两个相等的实数根 D、若a<0,则方程没有实数根8. 用反证法证明“三角形中至少有一个内角大于或等于60°”时,应假设( )A、三角形的二个内角小于60° B、三角形的三个内角都小于60° C、三角形的二个内角大于60° D、三角形的三个内角都大于60°9. 已知点(x1 , y1)和点(x2 , y2)在反比例函数y= (k<0)的图象上,若x1<x2 , 则( )A、(x1+x2)(y1+y2)<0 B、(x1+x2)(y1+y2)>0 C、x1x2(x1-x2)(y1-y2)<0 D、x1x2(x1-x2)(y1-y2)>010. 如图,在正方形ABCD中,点E是边BC上的一个动点(不与点B,C重合),AE的垂直平分线分别交AB,CD于点G,F.若CF=6DF,则BE:EC的值为( )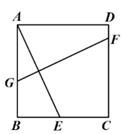 A、 B、 C、 D、
A、 B、 C、 D、二、认真填一填(本题有6个小题,每小题4分,共24分.)
-
11. 计算: = .12. 一元二次方程(x+3)2-2=0的根是 .13. 若一组数据1,3,a,2,5的平均数是3,则a= , 这组数据的方差是 .14. 如图,在五边形ABCDE中,∠A+∠E+∠D=330°,∠ABC和∠BCD的平分线交于点O,则∠BOC的度数为.
 15. 如图,在矩形ABCD中,点P在对角线AC上,过点P作EF∥BC,分别交AB,CD于点E,F,连结PB,PD.若PB= ,PD=6,图中阴影部分的面积为9,则矩形ABCD的周长为 .
15. 如图,在矩形ABCD中,点P在对角线AC上,过点P作EF∥BC,分别交AB,CD于点E,F,连结PB,PD.若PB= ,PD=6,图中阴影部分的面积为9,则矩形ABCD的周长为 . 16. 已知一次函数y=ax+b,反比例函数y= (a,b,k是常数,且ak≠0),若其中一部分x,y的对应值如下表,则不等式-8<ax+b< 的解集是 .
16. 已知一次函数y=ax+b,反比例函数y= (a,b,k是常数,且ak≠0),若其中一部分x,y的对应值如下表,则不等式-8<ax+b< 的解集是 .x
-4
-2
-1
1
2
4
y=ax+b
-6
-4
-3
-1
0
2
y=
-2
-4
-8
8
4
2
三、全面答一答(本题有7个小题,共66分.)
-
17. 计算:(1)、(2)、18. 解方程:(1)、(x+2)2=3(x+2)(2)、2x2+6x+3=019. 据某市交通运管部门5月份的最新数据,日前该市市面上的共享单车数量己达39万辆,共享单车也逐渐成为高校学生喜爱的“绿色出行”方式之一.某高校为了解本校学生出行使用共享单车的情况,随机调查了某天部分出行学生使用共享单车的情况,并整理成如下统计表.
使用次数
0
1
2
3
4
人数
8
10
22
26
14
(1)、求这天部分出行学生使用共享单车次数的平均数,中位数和众数.(2)、若该校这天有720名学生山行,估计使用共享单车次数在2次以上(含2次)的学生数.20. 随着科技水平的提高,某种电子产品的价格呈下降趋势,今年年底的价格是两年前的 ,假设从去年开始,连续三年(去年,今年,明年)该电子产品的价格下降率都相同.(1)、求这种电子产品的价格在这三年中的平均下降率.(2)、若两年前这种电子产品的价格是a元,请预测明年该电子产品的价格.21. 如图,在 ABCD中,点E,F是直线BD上的两点,DE=BF,连结AE,AF,CE,CF.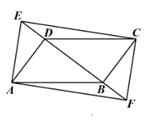 (1)、求证:四边形AFCE是平行四边形.(2)、若BD⊥AD,AB=5,AD=3,四边形AFCE是矩形,求DE的长.22. 为预防传染病,某校定期对教室进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量y(mg)与药物在空气中的持续时间x(min)成正比例;燃烧后,y与x成反比例(如图所示).现测得药物10分钟燃完,此时教室内每立方米空气含药量为8mg.根据以上信息解答下列问题:
(1)、求证:四边形AFCE是平行四边形.(2)、若BD⊥AD,AB=5,AD=3,四边形AFCE是矩形,求DE的长.22. 为预防传染病,某校定期对教室进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量y(mg)与药物在空气中的持续时间x(min)成正比例;燃烧后,y与x成反比例(如图所示).现测得药物10分钟燃完,此时教室内每立方米空气含药量为8mg.根据以上信息解答下列问题: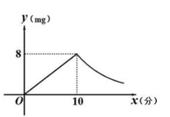 (1)、分别求出药物燃烧时及燃烧后y关于x的函数表达式.(2)、当每立方米空气中的含药量低于1.6mg时,对人体方能无毒害作用,那么从消毒开始,在哪个时段消毒人员不能停留在教室里?(3)、当室内空气中的含药量每立方米不低于3.2mg的持续时间超过20分钟,才能有效杀灭某种传染病毒.试判断此次消毒是否有效,并说明理由.23. 如图,在菱形ABCD中,AE⊥BC于点E.
(1)、分别求出药物燃烧时及燃烧后y关于x的函数表达式.(2)、当每立方米空气中的含药量低于1.6mg时,对人体方能无毒害作用,那么从消毒开始,在哪个时段消毒人员不能停留在教室里?(3)、当室内空气中的含药量每立方米不低于3.2mg的持续时间超过20分钟,才能有效杀灭某种传染病毒.试判断此次消毒是否有效,并说明理由.23. 如图,在菱形ABCD中,AE⊥BC于点E. (1)、若∠BAE=30°,AE=3,求菱形ABCD的周长.(2)、作AF⊥CD于点F,连结EF,BD,求证:EF∥BD.(3)、设AE与对角线BD相交于点G,若CE=4,BE=8,四边形CDGE和△AGD的面积分别是S1和S2 , 求S1-S2是的值.
(1)、若∠BAE=30°,AE=3,求菱形ABCD的周长.(2)、作AF⊥CD于点F,连结EF,BD,求证:EF∥BD.(3)、设AE与对角线BD相交于点G,若CE=4,BE=8,四边形CDGE和△AGD的面积分别是S1和S2 , 求S1-S2是的值.