浙江省嘉兴市2018-2019学年七年级下学期数学期末考试试卷

试卷更新日期：2019-07-04 类型：期末考试

进入出卷网下载

一、单选题(共10题，共30分)

1. (x²y)³的结果是（）

A、x⁵y³ B、x⁶y C、3x²y D、x⁶y³

查看试题解析
2. 如图，若∠A=∠D，则AB∥CD，判断依据是（）

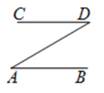A、两直线平行，同位角相等 B、两直线平行，内错角相等 C、同位角相等，两直线平行 D、内错角相等，两直线平行

查看试题解析
3. 下面式子从左边到右边的变形是因式分解的是（）

A、x²-x-2=x(x-1)-2 B、(a+b)(a-b)=a²-b² C、x²-4=(x+2)(x-2) D、x-1=x(1- $\frac{1}{x}$ )

查看试题解析
4. 若(x-3)(x+5)是x²+px+q的因式，则p为（）

A、-15 B、-2 C、8 D、2

查看试题解析
5. 如图，在网格中，每个小方格的边长均为1个单位，将图形E平移到另一个位置后能与图形F组合成一个正方形，下面平移步骤正确的是（）

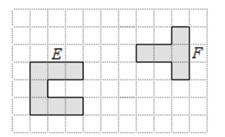A、先把图形E向右平移4个单位，再向上平移3个单位 B、先把图形E向右平移5个单位，再向上平移2个单位 C、先把图形E向右平移5个单位，再向上平移3个单位 D、先把图形E向右平移6个单位，再向上平移2个单位

查看试题解析
6. 计算：(12x³-8x²+16x)÷(-4x)的结果是（）

A、-3x²+2x-4 B、-3x²-2x+4 C、-3x²+2x+4 D、3x²-2x+4

查看试题解析
7. 某中学向西部山区一中学某班捐了若干本图书.如果该班每位同学分47本，那么还差3本；如果每位同学分45本，那么又多出43本，则该班共有学生（）名.

A、20 B、21 C、22 D、23

查看试题解析
8. 根据2010～2014年杭州市实现地区生产总值(简称GDP，单位：亿元)统计图所提供的信息(如图所示)，下列判断正确的是（）

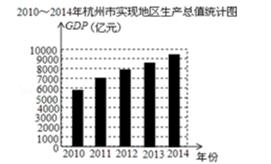A、2010-2014年杭州市每年GDP增长率相同 B、2014年杭州市的GDP比2010年翻一番 C、2010年杭州市的GDP未达到5400亿元 D、2010-2014年杭州市的GDP逐年增长

查看试题解析
9. A，B两地相距160千米，甲车和乙车的平均速度之比为4：5，两车同时从A地出发到B地，乙车比甲车早到30分钟，若求甲车的平均速度，设甲车平均速度为4x千米／小时，则所列方程是（）

A、 $\frac{160}{4 x} - \frac{160}{5 x} = 30$ B、 $\frac{160}{4 x} - \frac{160}{5 x} = \frac{1}{2}$ C、 $\frac{160}{5 x} - \frac{160}{4 x} = \frac{1}{2}$ D、 $\frac{160}{4 x} + \frac{160}{5 x} = 30$

查看试题解析
10. 已知关于x，y的方程组 ${\begin{cases} 3 x - 5 y = 2 a \\ x - 2 y = a - 5 \end{cases}$ ，则下列结论中正确的个数有（）
①当a=10时，方程组的解是 ${\begin{cases} x = 15 \\ y = 5 \end{cases}$ ；②当x，y的值互为相反数时，a=20；③不存在一个实数a使得x=y；④若3^x-3a=3⁵ ，则a=5

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题(共10题，共30分)

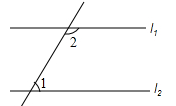
11. 如图，若l₁∥l₂ ， ∠1=x°，则∠2= .

查看试题解析
12. 计算：(-2a²)²=；
2x²·(-3x³)=.

查看试题解析
13. 禽流感病毒的直径约为0.000 002 05 cm，用科学记数法表示为 cm；

查看试题解析
14. 因式分解x³-xy²= .

查看试题解析
15. 在一样本容量为80的样本中，已知某组数据的频率为0.7，频数为 .

查看试题解析
16. 计算 $\frac{b}{a^{2} - b^{2}} \div (1 - \frac{a}{a + b})$ 的结果是．

查看试题解析
17. 已知 ${\begin{cases} x = a \\ y = b \end{cases}$ 是方程组 ${\begin{cases} x - 2 y = 0 \\ 2 x + y = 5 \end{cases}$ 的解，则3a-b=.

查看试题解析
18. 若方程 $\frac{m - 1}{x + 2} - \frac{1}{x + 2} = 2$ 有增根，则m的值为 .

查看试题解析
19. 在日常生活中如取款、上网等都需要密码，有一种用“因式分解法”产生的密码，方便记忆，原理是对于多项x⁴-y⁴ ，因式分解的结果是(x-y)(x+y)(x²+y²)，若取x=9，y=9时，则各个因式值是：(x+y)=18，(x-y)=0，(x²+y²)=162,于是就可以把“180162”作为一个六位数的密码，对于多项式9x³-xy² ，取x=10，y=10时，用上述方法产生的密码是(写出一个即可).

查看试题解析
20. 某水果店销售50千克香蕉，第一天售价为9元／千克，第二天降价为6元／千克，第三天再降为3元／千克.三天全部售完，共计所得270元，若该店第二天销售香蕉t千克，则第三天销售香蕉千克.(用含t的代数式表示.)

查看试题解析

三、解答题(共6题，共40分)

21. 解方程(组)：

(1)、 ${\begin{cases} 2 x - 5 y = 12 \\ 4 x + 3 y = - 2 \end{cases}$

(2)、 $\frac{1}{3 - x} - 2 = \frac{2 - x}{x - 3}$

查看试题解析
22. 如图，AB∥CD，∠A=60°，∠C=∠E，求∠E.

查看试题解析
23. 在大课间活动中，同学们积极参加体育锻炼，小龙在全校随机抽取一部分同学就“我最喜爱的体育项目”进行了一次抽样调查，下面是他通过收集的数据绘制的两幅不完整的统计图，请你根据图中提供的信息，解答以下问题：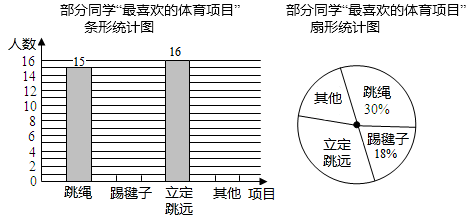

(1)、小龙共抽取名学生。

(2)、补全条形统计图；

(3)、在扇形统计图中，“其他”部分对应的圆心角的度数是；

(4)、若全校共2100名学生，请你估算“立定跳远”部分的学生人数.

查看试题解析
24. 某服装店购进一批甲、乙两种款型的时尚T恤衫，甲种款型共用了7800元，乙种款型共用了6 400元，甲种款型的件数是乙种款型件数的1.5倍，甲种款型每件的进价比乙种款型每件的进价少30元

(1)、甲、乙两种款型的T恤衫各购进多少件?

(2)、商店按进价提高60％标价销售，销售一段时间后，甲款型全部售完，乙款型剩余一半，商店决定对乙款型按标价的五折销售，很快全部售完.求售完这批T恤衫商店共获利多少元?

查看试题解析
25. 某校七年级400名学生到郊外参加植树活动，已知用2辆小客车和1辆大客车每次可运送学生85人，用3辆小客车和2辆大客车每次可运送学生150人.

(1)、每辆小客车和每辆大客车各能坐多少名学生?

(2)、若计划租小客车m辆，大客车n辆，一次送完，且恰好每辆车都坐满：
①请你设计出所有的租车方案；

②若小客车每辆租金300元，大客车每辆租金500元，请选出最省线的租车方案，并求出最少租金.

查看试题解析
26. 【阅读与思考】
整式乘法与因式分解是方向相反的变形.如何把二次_一项式ax²+bx+c进行因式分解呢?我们已经知道，(a₁x+c₁)(a₂x+c₂)=a₁a₂x²+a₁c₂x+a₂c₁x+c₁c₂=a₁a₂x²+(a₁c₂+a₂c₁)x+c₁c₂.反过来，就得到：a₁a₂x²+(a₁c₂+a₂c₁)x+c₁c₂=(a₁x+c₁)(a₂x+c₂).

我们发现，二次项的系数a分解成a₁a₂ ，常数项c分解成c₁c₂ ，并且把a₁ ， a₂ ， c₁ ， c₂ ，如图①所示摆放，按对角线交叉相乘再相加，就得到a₁c₂+a₂c₁ ，如果a₁c₂+a₂c₁的值正好等于ax²+bx+c的一次项系数b，那么ax²+bx+c就可以分解为(a₁x+c₁)(a₂x+c₂)，其中a₁ ， c₁位于图的上一行，a₂ ， c₂位于下一行.

像这种借助画十字交叉图分解系数，从而帮助我们把二次三项式分解因式的方法，通常叫做“十字相乘法”.

例如，将式子x²-x-6分解因式的具体步骤为：首先把二次项的系数1分解为两个因数的积，即1=1×1，把常数项-6也分解为两个因数的积，即-6=2×（-3)；然后把1，1，2，-3按图②所示的摆放，按对角线交叉相乘再相加的方法，得到1×(-3)+1×2=-1，恰好等于一次项的系数-1，于是x²-x-6就可以分解为(x+2)(x-3).

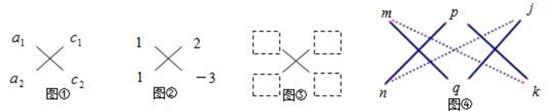(1)、请同学们认真观察和思考，尝试在图③的虚线方框内填入适当的数，并用“十字相乘法”分解因式：x²+x-6=.

(2)、【理解与应用】
请你仔细体会上述方法，并尝试对下面两个二次三项式进行分解因式：

Ⅰ.2x²+5x-7=；

Ⅱ.6x²-7xy+2y²= .

(3)、【探究与拓展】
对于形如ax²+bxy+cy²+dx+ey+f的关于x，y的二元二次多项式也可以用“十字相乘法”来分解.如图④，将a分解成mn乘积作为一列，c分解成pq乘积作为第二列，f分解成jk乘积作为第三列，如果mq+np=b，pk+qj=e，mk+nj=d，即第1，2列、第2，3列和第1，3列都满足十字相乘规则，则原式=(mx+py+j)(nx+qy+k)，请你认真阅读上述材料并尝试挑战下列问题：

Ⅰ.分解因式3x²+5xy-2y²+x+9y-4= .

Ⅱ.若关于x，y的二元二次式x²+7xy-18y²-5x+my-24 可以分解成两个一次因式的积，求m的值.

Ⅲ.已知x，y为整数，且满足x²+3xy+2y²+2x+3y=-1，请写出一组符合题意的x，y的值.

查看试题解析