浙江省嘉兴市2018-2019学年八年级下学期数学期末考试试卷

试卷更新日期：2019-07-04 类型：期末考试

进入出卷网下载

一、单选题(共10题，共30分)

1. 下列图形，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列各式中，正确的是（）

A、 ${\sqrt{{(- 2)}^{2}}}^{} = - 2$ B、 $- \sqrt{2^{2}} = - 2$ C、 ${(- \sqrt{2})}^{2} = - 2$ D、 $\sqrt{2^{2}} = \pm 2$

查看试题解析
3. 如果反比例函数y= $\frac{k - 1}{x}$ 的图象经过点(-1，-2)，则k的值是（）

A、2 B、-2 C、-3 D、3

查看试题解析
4. 方程(x-1)(x+2)=x-1的解是（）

A、x=-2 B、x₁=1，x₂=-2 C、x₁=-1，x₂=1 D、x₁=-1，x₂=3

查看试题解析
5. 某企业1~5月份利润的变化情况如图所示，则以下说法与图中反映的信息相符的是（）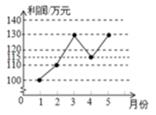

A、1~2月份利润的增长快于2~3月份利润的增长 B、1~4月份利润的方差与1~5月份利润的方差相同 C、1~5月份利润的众数是130万元 D、1~5月份利润的中位数为120万元

查看试题解析
6. 利用反证法证明命题“四边形中至少有一个角是钝角或直角”时，应假设（）

A、四边形中至多有一个内角是钝角或直角 B、四边形中所有内角都是锐角 C、四边形的每一个内角都是钝角或直角 D、四边形中所有内角都是直角

查看试题解析
7. 如图，在平面直角坐标系xOy中，已知点A( $\sqrt{2}$ ，0)，B(1，1).若平移点A到点C，使以点O，A，C，B为顶点的四边形是菱形，则正确的平移方法是（）

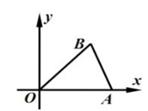A、向左平移1个单位，再向下平移1个单位 B、向左平移(2 $\sqrt{2}$ -1个单位，再向上平移1个单位 C、向右平移 $\sqrt{2}$ 个单位，再向上平移1个单位 D、向右平移1个单位，再向上平移1个单位

查看试题解析
8. 如图，将平行四边形纸片ABCD折叠，使顶点D恰好落在AB边上的点M处，折痕为AN，那么对于结论：①MN∥BC，②MN=AM.下列说法正确的是（）

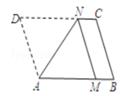A、①②都错 B、①对②错 C、①错②对 D、①②都对

查看试题解析
9. 已知实数x满足(x²-x)²-4(x²-x)-12=0，则代数式x²-x+1的值是（）

A、7 B、-1 C、7或-1 D、-5或3

查看试题解析
10. 如图，正方形ABCD在平面直角坐标系中的点A和点B的坐标为A(1，0)、B(0，3)，点D在双曲线y= $\frac{k}{x}$ (k≠0)上.若正方形沿x轴负方向平移m个单位长度后，点C恰好落在该双曲线上，则m的值是（）

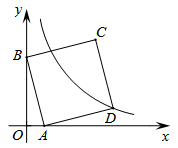A、1 B、2 C、3 D、4

查看试题解析

二、填空题(共10题，共30分)

11. 一组数据为1，2，3，4，5，6，则这组数据的中位数是 .

查看试题解析
12. 化简:4 $\sqrt{3}$ -7 $\sqrt{12}$ +2 $\sqrt{48}$ =.

查看试题解析
13. 若一个多边形的内角和比外角和多900°，则该多边形的边数是 .

查看试题解析
14. 已知反比例函数y= $\frac{6}{x}$ 在第一象限的图象如图所示，点A在其图象上，点B为x轴正半轴上一点，连结AO、AB，且AO=AB，则S_△_AOB= .

查看试题解析
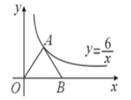15. 平行四边形的一个内角平分线将该平行四边形的一边分为3cm和4cm两部分，则该平行四边形的周长为 .

查看试题解析
16. 关于x的一元二次方程x²+2x- $\frac{1}{a}$ =0有实数根，则a的取值范围是 .

查看试题解析
17. 准备在一块长为30米，宽为24米的长方形花圃内修建四条宽度相等，且与各边垂直的小路，(如图所示)四条小路围成的中间部分恰好是一个正方形，且边长是小路宽度的4倍，若四条小路所占面积为80平方米，则小路的宽度为米 .

查看试题解析
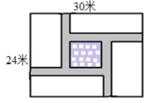18. 如图，矩形ABCD中，AD=5，AB=7.点E为DC上一个动点，把△ADE沿AE折叠，当点D的对应点D'落在∠ABC的角平分线上时，DE的长为.

查看试题解析
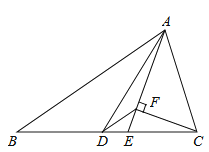
19.
如图，△ABC中，AD是中线，AE是角平分线，CF⊥AE于F ， AB=5，AC=2，则DF的长为.

查看试题解析
20. 如图，点A，B在反比例函数y= $\frac{k}{x}$ (k>0)的图象上，AC⊥x轴，BD⊥x轴，垂足C，D分别在x轴的正、负半轴上，CD=k，已知AB=2AC，E是AB的中点，且△BCE的面积是△ADE的面积的2倍，则k的值是

查看试题解析

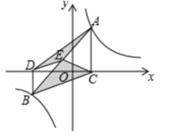
三、解答题(共6题，共40分)

21.

(1)、计算: $\sqrt{{(- 3)}^{2}} - (2 - \sqrt{3}) (2 + \sqrt{3}) - \sqrt{8}$

(2)、解方程:x²+6x+8=0

查看试题解析
22. 某市射击队甲、乙两名队员在相同的条件下各射靶10次，每次射靶的成绩情况如图所示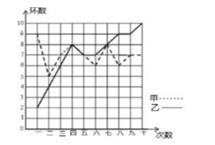

(1)、请将下表补充完整：(参考公式：方差S²= $\frac{1}{n}$ [ (x₁- $\bar{x}$ )²+(x₂- $\bar{x}$ )²+…+(x_n- $\bar{x}$ )²])

平均数

方差

中位数

甲

7

7

乙

5.4

(2)、请从下列三个不同的角度对这次测试结果进行分析：
①从平均数和方差相结合看，的成绩好些

②从平均数和中位数相结合看，的成绩好些

③若其他队选手的最好成绩在9环左右，现要选一人参赛，你认为选谁参加，并说明理由。

查看试题解析
23. 已知一艘轮船上装有100吨货物，轮船到达目的地后开始卸货.设平均卸货速度为ν(单位:吨/小时)，卸完这批货物所需的时间为t(单位:小时)

(1)、求v关于t的函数表达式

(2)、若要求不超过5小时卸完船上的这批货物，那么平均每小时至少要卸货多少吨?

查看试题解析
24. 图1，图2，图3是三张形状和大小完全相同的方格纸，方格纸中每个小正方形的边长均为1，A，C两点都在格点上，连结AC，请完成下列作图：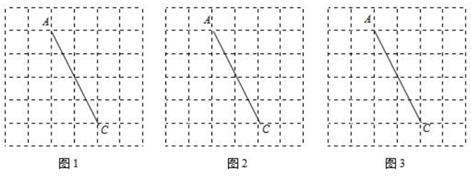

(1)、以AC为对角线在图1中作一个正方形，且正方形各顶点均在格点上

(2)、以AC为对角线在图2中作一个矩形，使得矩形面积为6，且矩形各顶点均在格点上

(3)、以AC为对角线在图3中作一个面积最小的平行四边形，且平行四边形各顶点均在格点上

查看试题解析
25. 如图，在平面直角坐标系中，O是原点， $▱$ ABCO的顶点A、C的坐标分别为A(-3，0)、C(1，2)，反比例函数y= $\frac{k}{x}$ (k≠0)的图象经过点B

(1)、求点B的坐标；

(2)、求k的值

(3)、将 $▱$ ABCO沿x轴翻折，点C落在点C'处.判断点C'是否落在反比例函数y= $\frac{k}{x}$ (k≠0)的图象上，请通过计算说明理由

查看试题解析
26. 如图，在长方形ABCD中，AB=6cm，AD=2cm，动点P、Q分别从点A、C同时出发，点P以2厘米/秒的速度向终点B移动，点Q以1厘米/秒的速度向D移动，当有一点到达终点时，另一点也停止运动.设运动的时间为t，问：

(1)、当t=1秒时，四边形BCQP面积是多少?

(2)、当t为何值时，点P和点Q距离是3cm?

(3)、当t= 时，以点P、Q、D为顶点的三角形是等腰三角形.(直接写出答案)

查看试题解析

	平均数	方差	中位数
甲	7		7
乙		5.4