广东省珠海市香洲区2018-2019学年中考数学模拟考试试卷

试卷更新日期：2019-07-03 类型：中考模拟

进入出卷网下载

一、单选题

1. ﹣2的绝对值是（）

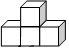
A、 $- 2$ B、 $2$ C、 $﹣ \frac{1}{2}$ D、 $\frac{1}{2}$

查看试题解析
2. 由4个小立方体搭成如图所示的几何体，从正面看到的平面图形是（）

A、 B、 C、 D、

查看试题解析
3. 下列计算正确的是（）

A、（a³）⁴＝a⁷ B、a³•a⁴＝a⁷ C、a³+a⁴＝a⁷ D、（ab）³＝ab³

查看试题解析
4. 如果 $\sqrt{x + 1}$ 是二次根式，那么x的取值范围（）

A、x＞﹣1 B、x≥﹣1 C、x≥0 D、x＞0

查看试题解析
5. 如图，直线l₁、l₂被直线l₃所截，下列选项中哪个不能得到l₁∥l₂？（）

A、∠1＝∠2 B、∠2＝∠3 C、∠3＝∠5 D、∠3+∠4＝180°

查看试题解析
6. 一组数据：2，1，2，5，7，5，x，它们的众数为2，则这组数据的中位数是（）

A、1 B、2 C、5 D、7

查看试题解析
7. 如图，⊙O的直径AB长为10，弦BC长为6，OD⊥AC，垂足为点D，则OD长为（）

A、6 B、5 C、4 D、3

查看试题解析
8. 已知方程x﹣2y+3＝8，则整式x﹣2y+1的值为（）

A、4 B、5 C、6 D、7

查看试题解析
9. 用A，B两个机器人搬运化工原料，A机器人比B机器人每小时多搬运30kg，A机器人搬运900kg所用时间与B机器人搬运600kg所用时间相等，设A机器人每小时搬运xkg化工原料，那么可列方程（）

A、 $\frac{900}{x}$ ＝ $\frac{600}{x - 3}$ B、 $\frac{900}{x + 3}$ ＝ $\frac{600}{x}$ C、 $\frac{600}{x + 30}$ ＝ $\frac{900}{x}$ D、 $\frac{900}{x - 3}$ ＝ $\frac{600}{x}$

查看试题解析
10. 如图，平行四边形AOBC中，∠AOB＝60°，AO＝8，AC＝15，反比例函数y＝ $\frac{k}{x}$ （x＞0）图象经过点A，与BC交于点D，则 $\frac{B D}{O A}$ 的值为（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{\sqrt{3}}{3}$

查看试题解析

二、填空题

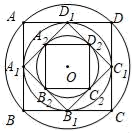
11. 港珠澳大桥世界闻名，连接香港大屿山、澳门半岛和广东省珠海市，总长约55000米，2018年10月24日上午9时正式通车，用科学记数法表示55000米应为米．

查看试题解析
12. 一个多边形的内角和是720°，这个多边形的边数是．

查看试题解析
13. 分解因式： $x^{3} - 4 x$ =

查看试题解析
14. 不等式组 ${\begin{matrix} 2 x - 3 \geq 1 \\ 3 - x < 0 \end{matrix}$ 的解集是．

查看试题解析
15. 直角三角形的一条直角边和斜边的长分别是一元二次方程x²﹣5x+6＝0的两个实数根，该直角三角形的面积是．

查看试题解析
16. 如图，作半径为2的⊙O的内接正四边形ABCD，然后作正四边形ABCD的内切圆，得第二个圆，再作第二个圆的内接正四边形A₁B₁C₁D₁ ，又作正四边形A₁B₁C₁D₁的内切圆，得第三个圆…，如此下去，则第六个圆的半径为．

查看试题解析

三、解答题

17. 计算： $\sqrt{16}$ ﹣（π﹣2019）⁰+2^﹣¹ ．

查看试题解析
18. 先化简，再求值： $\frac{a - 1}{a^{2} - 1}$ ÷ $\frac{a + 2}{a^{2} + 2 a + 1}$ ﹣ $\frac{a}{a + 2}$ ，其中a＝ $\sqrt{3}$ ．

查看试题解析
19. 如图，锐角△ABC中，AB＝8，AC＝5．

(1)、请用尺规作图法，作BC的垂直平分线DE，垂足为E，交AB于点D（不要求写作法，保留作图痕迹）；

(2)、在（1）的条件下，连接CD，求△ACD周长．

查看试题解析
20. 某水果批发市场规定，批发苹果不少于100kg时，批发价为10元/kg．小王携带现金3000元到该市场采购苹果，并以批发价买进．设购买的苹果为xkg，小王付款后还剩余现金y元．

(1)、试写出y关于x的函数解析式，并写出自变量x的取值范围；

(2)、若小王付款后还剩余现金1200元，问小王购买了苹果多少kg？

查看试题解析
21. 某校开设有STEAM（A类）、音乐（B类）、体育（C类）、舞蹈（D类）四类社团活动，要求学生全员参加，每人限报一类．为了了解学生参与社团活动的情况，校学生会随机抽查了部分学生，将所收集的数据绘制成如图所示不完整的统计图．请根据图中提供的信息解答下列问题：

类型

频数

频率

A

30

x

B

18

0.15

C

m

0.40

D

n

y

(1)、x＝，并补全条形统计图；

(2)、若该校共有1800人，报STEAM的有人；

(3)、如果学生会想从D类的甲、乙、丙三人中随机选择两人参加舞蹈演出，请用列表法或树状图的方法求出恰好选中甲的概率．

查看试题解析
22. 如图，将等边△ABC绕点C顺时针旋转90°得到△EFC，∠ACE的平分线CD交EF于点D，连接AD、AF．

(1)、求∠CFA度数；

(2)、求证：AD∥BC．

查看试题解析
23. 如图1，将抛物线P₁：y₁＝ $\frac{1}{3}$ x²﹣3右移m个单位长度得到新抛物线P₂：y₂＝a（x+h）²+k，抛物线P₁与x轴交于A、B两点，与y轴交于点C，抛物线P₂与x轴交于A₁ ， B₁两点，与y轴交于点C₁ ．

(1)、当m＝1时，a＝， h＝， k＝；

(2)、在（1）的条件下，当y₁＜y₂＜0时，求x的取值范围；

(3)、如图2，过点C₁作y轴的垂线，分别交抛物线P₁ ， P₂于D、E两点，当四边形A₁DEB是矩形时，求m的值．

查看试题解析
24. 如图，△ABC内接于半径为 $\sqrt{5}$ 的⊙O，AC为直径，AB＝ $\sqrt{10}$ ，弦BD与AC交于点E，点P为BD延长线上一点，且∠PAD＝∠ABD，过点A作AF⊥BD于点F，连接OF．

(1)、求证：AP是⊙O的切线；

(2)、求证：∠AOF＝∠PAD；

(3)、若tan∠PAD＝ $\frac{1}{3}$ ，求OF的长．

查看试题解析
25. 如图1，菱形ABCD中，DE⊥AB，垂足为E，DE＝3cm，AE＝4cm，把四边形BCDE沿DE所在直线折叠，使点B落在AE上的点M处，点C落在点N处，MN交AD于点F．

(1)、证明：FA＝FM；

(2)、求四边形DEMF面积；

(3)、如图2，点P从点D出发，沿D→N→F路径以每秒1cm的速度匀速运动，设运动时间为t秒，当t为何值时，△DPF的面积与四边形DEMF的面积相等．

查看试题解析

类型	频数	频率
A	30	x
B	18	0.15
C	m	0.40
D	n	y