广东省肇庆市怀集县2018-2019学年中考数学二模考试试卷
试卷更新日期:2019-07-03 类型:中考模拟
一、单选题
-
1. 如图是五个大小相同的正方体组成的几何体,这个几何体的俯视图是( )
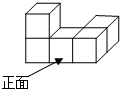 A、
A、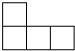 B、
B、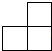 C、
C、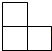 D、
D、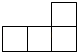 2. 下列所给的汽车标志图案中,既是轴对称图形,又是中心对称图形的是( )A、
2. 下列所给的汽车标志图案中,既是轴对称图形,又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 3. 中国倡导的“一带一路”建设将促进我国与世界各国的互利合作,根据规划“一带一路”地区覆盖总人口44亿,这个数用科学记数法表示为( )A、44×108 B、4.4×109 C、4.4×108 D、4.4×10104. 下列计算正确的是( )A、x2﹣3x2=﹣2x4 B、(﹣3x2)2=6x2 C、x2y•2x3=2x6y D、6x3y2÷(3x)=2x2y25. 一个正多边形的每一个外角都等于45°,则这个多边形的边数为( )A、4 B、6 C、8 D、106. 将一副三角板(∠A=30°)按如图所示方式摆放,使得AB∥EF,则∠1等于( )
3. 中国倡导的“一带一路”建设将促进我国与世界各国的互利合作,根据规划“一带一路”地区覆盖总人口44亿,这个数用科学记数法表示为( )A、44×108 B、4.4×109 C、4.4×108 D、4.4×10104. 下列计算正确的是( )A、x2﹣3x2=﹣2x4 B、(﹣3x2)2=6x2 C、x2y•2x3=2x6y D、6x3y2÷(3x)=2x2y25. 一个正多边形的每一个外角都等于45°,则这个多边形的边数为( )A、4 B、6 C、8 D、106. 将一副三角板(∠A=30°)按如图所示方式摆放,使得AB∥EF,则∠1等于( )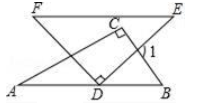 A、75° B、90° C、105° D、115°7. 如图是根据某班40名同学一周的体育锻炼情况绘制的统计图,该班40名同学一周参加体育锻炼时间的中位数,众数分别是( )
A、75° B、90° C、105° D、115°7. 如图是根据某班40名同学一周的体育锻炼情况绘制的统计图,该班40名同学一周参加体育锻炼时间的中位数,众数分别是( ) A、10.5,16 B、8.5,16 C、8.5,8 D、9,88. 如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为4,∠B=135°,则劣弧AC的长是( )
A、10.5,16 B、8.5,16 C、8.5,8 D、9,88. 如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为4,∠B=135°,则劣弧AC的长是( ) A、4π B、2π C、π D、9. 小芳在本学期的体育测试中,1分钟跳绳获得了满分,她的“满分秘籍”如下:前20秒由于体力好,小芳速度均匀增加,20秒至50秒保持跳绳速度不变,后10秒进行冲刺,速度再次均匀增加,最终获得满分,反映小芳1分钟内跳绳速度y(个/秒)与时间t(秒)关系的函数图象大致为( )A、
A、4π B、2π C、π D、9. 小芳在本学期的体育测试中,1分钟跳绳获得了满分,她的“满分秘籍”如下:前20秒由于体力好,小芳速度均匀增加,20秒至50秒保持跳绳速度不变,后10秒进行冲刺,速度再次均匀增加,最终获得满分,反映小芳1分钟内跳绳速度y(个/秒)与时间t(秒)关系的函数图象大致为( )A、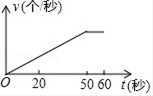 B、
B、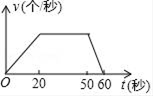 C、
C、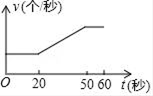 D、
D、 10. 如图,把长方形纸片ABCD沿对角线折叠,设重叠部分为△EBD,那么,有下列说法:①△EBD是等腰三角形,EB=ED;②折叠后∠ABE和∠CBD一定相等;③折叠后得到的图形是轴对称图形;④△EBA和△EDC一定是全等三角形.其中正确的是( )
10. 如图,把长方形纸片ABCD沿对角线折叠,设重叠部分为△EBD,那么,有下列说法:①△EBD是等腰三角形,EB=ED;②折叠后∠ABE和∠CBD一定相等;③折叠后得到的图形是轴对称图形;④△EBA和△EDC一定是全等三角形.其中正确的是( ) A、①②③ B、①③④ C、①②④ D、①②③④
A、①②③ B、①③④ C、①②④ D、①②③④二、填空题
-
11. 计算:﹣1+2= .12. 分解因式:m3﹣m= .13. 将y=2x2的图象沿y轴向下平移3个单位,则得到的新图象所对应的函数表达式为 .14. 如图,AB∥CD , AB= CD , S△ABO:S△CDO= .
 15. 《九章算术》中记载:“今有牛五、羊二,直金十两;牛二、羊五,直金八两.问:牛、羊各直金几何?”
15. 《九章算术》中记载:“今有牛五、羊二,直金十两;牛二、羊五,直金八两.问:牛、羊各直金几何?”译文:“假设有5头牛、2只羊,值金10两;2头牛、5只羊,值金8两.问:每头牛、每只羊各值金多少两?”设每头牛值金x两,每只羊值金y两,可列方程组为 .
16. 如图,用圆心角为120°,半径为6cm的扇形纸片卷成一个圆锥形无底纸帽,则这个纸帽的高是cm .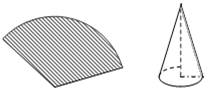
三、解答题
-
17. 计算:2sin30°+ ﹣2019018. 先化简,再求值:(2﹣ )÷ ,其中x=2.19. 如图,在锐角△ABC中,AB=2cm , AC=3cm .
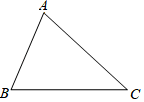
(1)、尺规作图:作BC边的垂直平分线分别交AC , BC于点D、E(保留作图痕迹,不要求写作法);(2)、在(1)的条件下,连结BD , 求△ABD的周长.
20. 如图,甲、乙两座建筑物的水平距离 为 ,从甲的顶部 处测得乙的顶部 处的俯角为 ,测得底部 处的俯角为 ,求甲、乙建筑物的高度 和 (结果取整数).参考数据: , .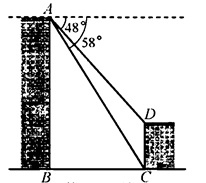 21. 中华文化源远流长,文学方面,《西游记》、《三国演义》、《水浒传》、《红楼梦》是我国古代长篇小说中的典型代表,被称为“四大古典名著”某中学为了解学生对四大名著的阅读情况,就“四大古典名著你读完了几部”的问题在全校学生中进行了抽样调查,根据调查结果绘制成如下尚不完整的统计图.
21. 中华文化源远流长,文学方面,《西游记》、《三国演义》、《水浒传》、《红楼梦》是我国古代长篇小说中的典型代表,被称为“四大古典名著”某中学为了解学生对四大名著的阅读情况,就“四大古典名著你读完了几部”的问题在全校学生中进行了抽样调查,根据调查结果绘制成如下尚不完整的统计图.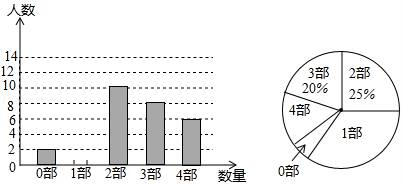
请根据以上信息,解决下列问题
(1)、本次调查所得数据的众数是部,中位数是部;(2)、扇形统计图中“4部”所在扇形的圆心角为度;(3)、请将条形统计图补充完整;(4)、没有读过四大古典名著的两名学生准备从中各自随机选择一部来阅读,求他们恰好选中同一名著的概率.22. 如图,在平行四边形ABCD中,点E、F分别在AB、CD上,且ED⊥DB,FB⊥BD.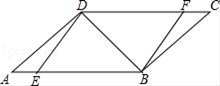 (1)、求证:△AED≌△CFB;(2)、若∠A=30°,∠DEB=45°,求证:DA=DF.23. 如图,以AB为直径作⊙O , 过点A作⊙O的切线AC , 连结BC , 交⊙O于点D , 点E是BC边的中点,连结AE .
(1)、求证:△AED≌△CFB;(2)、若∠A=30°,∠DEB=45°,求证:DA=DF.23. 如图,以AB为直径作⊙O , 过点A作⊙O的切线AC , 连结BC , 交⊙O于点D , 点E是BC边的中点,连结AE .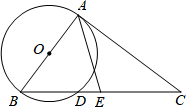 (1)、求证:∠AEB=2∠C;(2)、若AB=6,cosB= ,求DE的长.24. 已知,抛物线y=ax2+ax+b(a≠0)与直线y=2x+m有一个公共点M(1,0),且a<b.
(1)、求证:∠AEB=2∠C;(2)、若AB=6,cosB= ,求DE的长.24. 已知,抛物线y=ax2+ax+b(a≠0)与直线y=2x+m有一个公共点M(1,0),且a<b.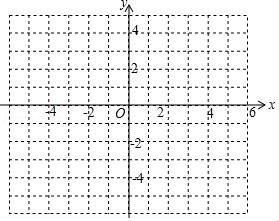 (1)、求b与a的关系式和抛物线的顶点D坐标(用a的代数式表示);(2)、直线与抛物线的另外一个交点记为N,求△DMN的面积与a的关系式;(3)、a=﹣1时,直线y=﹣2x与抛物线在第二象限交于点G,点G、H关于原点对称,现将线段GH沿y轴向上平移t个单位(t>0),若线段GH与抛物线有两个不同的公共点,试求t的取值范围.25. 如图,矩形ABCD中,AB=4,BC=6,E是BC边的中点,点P在线段AD上,过P作PF⊥AE于F,设PA=x.
(1)、求b与a的关系式和抛物线的顶点D坐标(用a的代数式表示);(2)、直线与抛物线的另外一个交点记为N,求△DMN的面积与a的关系式;(3)、a=﹣1时,直线y=﹣2x与抛物线在第二象限交于点G,点G、H关于原点对称,现将线段GH沿y轴向上平移t个单位(t>0),若线段GH与抛物线有两个不同的公共点,试求t的取值范围.25. 如图,矩形ABCD中,AB=4,BC=6,E是BC边的中点,点P在线段AD上,过P作PF⊥AE于F,设PA=x.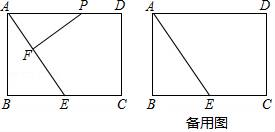 (1)、求证:△PFA∽△ABE;(2)、当点P在线段AD上运动时,设PA=x,是否存在实数x,使得以点P,F,E为顶点的三角形也与△ABE相似?若存在,请求出x的值;若不存在,请说明理由;(3)、探究:当以D为圆心,DP为半径的⊙D与线段AE只有一个公共点时,请直接写出x满足的条件:.
(1)、求证:△PFA∽△ABE;(2)、当点P在线段AD上运动时,设PA=x,是否存在实数x,使得以点P,F,E为顶点的三角形也与△ABE相似?若存在,请求出x的值;若不存在,请说明理由;(3)、探究:当以D为圆心,DP为半径的⊙D与线段AE只有一个公共点时,请直接写出x满足的条件:.