广东省汕头市潮南区2018-2019学年中考数学模拟考试试卷

试卷更新日期：2019-07-03 类型：中考模拟

进入出卷网下载

一、单选题

1. 一元二次方程 $4 x^{2} + \frac{1}{4} = 0$ 的根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、有两个实数根

查看试题解析
2. 不透明的袋子中装有形状、大小、质地完全相同的 $6$ 个球，其中 $4$ 个黑球， $2$ 个白球，从袋子中一次摸出 $3$ 个球，下列事件是不可能事件的是（）

A、摸出的是 $2$ 个黑球， $1$ 个白球 B、摸出的是 $3$ 个黑球 C、摸出的是 $2$ 个白球， $1$ 个黑球 D、摸出的是 $3$ 个白球

查看试题解析
3. 如图所示的几何体的俯视图是（）

A、 B、 C、 D、

查看试题解析
4. 若二次函数y=ax²的图象经过点P(-2，4)，则该图象必经过点( )

A、(2，4) B、(-2，-4) C、(-4，2) D、(4，-2)

查看试题解析
5. 将一图形绕着点 $O$ 顺时针方向旋转 $70^{\circ}$ 后，再绕着点 $O$ 逆时针方向旋转 $120^{\circ}$ ，这时如果要使图形回到原来的位置，需要将图形绕着点 $O$ 什么方向旋转多少度?（）

A、逆时针方向， $50^{\circ}$ B、顺时针方向， $50^{\circ}$ C、顺时针方向， $190^{\circ}$ D、逆时针方向， $190^{\circ}$

查看试题解析
6. 平面直角坐标系，⊙ $P$ 的圆心坐标为 $(4, 8)$ ，半径为 $5$ ，那么 $x$ 轴与⊙ $P$ 的位置关系是（）

A、相交 B、相离 C、相切 D、以上都不是

查看试题解析
7. 如图，已知 $A B / / C D / / E F$ ，那么下列结论正确的是（）

A、 $\frac{A D}{D F} = \frac{B C}{C E}$ B、 $\frac{B C}{C E} = \frac{D F}{A D}$ C、 $\frac{C D}{E F} = \frac{B C}{B E}$ D、 $\frac{C D}{E F} = \frac{A D}{A F}$

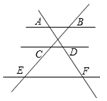查看试题解析
8. 已知反比例函数 $y = - \frac{2}{x}$ ，下列说法错误的是（）

A、图像必经过点 $(- 1 ， 2)$ B、 $y$ 随着 $x$ 的增大而增大 C、图像分布在第二，四象限内 D、若 $x > 1$ ，则 $- 2 < y < 0$

查看试题解析
9. 已知锐角 $A$ 满足关系式 $2 {sin}^{2} A - 7 sin A + 3 = 0$ ，则 $sin A$ 的值为（）

A、 $\frac{1}{2}$ 或 $3$ B、 $3$ C、 $\frac{1}{2}$ D、 $4$

查看试题解析
10. 如图，在半径为5的⊙O中，AB、CD是互相垂直的两条弦，垂足为P，且AB=CD=8，则OP的长为（）

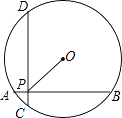A、3 B、4 C、3 $\sqrt{2}$ D、4 $\sqrt{2}$

查看试题解析

二、填空题

11. 二次函数 $y = - {(x + 1)}^{2} - 4$ 的最大值为．

查看试题解析
12. 已知△ABC∽△A′B′C′且S_△_ABC:S_△_A_′_B_′_C_′＝1:2，则AB:A′B′＝．

查看试题解析
13. 若关于x的一元二次方程x²+mx+2n=0有一个根是2，则m+n= ．

查看试题解析
14. 在一个不透明的布袋中装有 $3$ 个蓝球和 $m$ 个黄球，它们除颜色不同外，其余均相同，若从中随机摸出一个球，摸到黄球的概率是 $\frac{5}{6}$ ，则 $m =$ ．

查看试题解析
15. 在 $R t Δ A B C$ 中， $∠ A C B = 90^{0} ， A C = 5 ， B C = 12$ ，现以 $B C$ 所在的直线为轴将 $Δ A B C$ 旋转一周，所得几何体的侧面积为．

查看试题解析
16. 如图，△OAC和△BAD都是等腰直角三角形，∠ACO=∠ADB=90°，反比例函数y= $\frac{k}{x}$ 在第一象限的图象经过点B，若OA²﹣AB²=8，则k的值为．

查看试题解析

三、解答题

17. 计算: $| - 2 | + 2 sin 30^{0} - {(- \sqrt{3})}^{2} + {(tan 45^{0})}^{- 1}$

查看试题解析
18. 如图所示的正方形网格中， $Δ A B C$ 的顶点均在格点上，在所给直角坐标系中解答下列问题；

(1)、作出 $Δ A B C$ 关于坐标原点成中心对称的 $Δ A {}_{1}B_{1} C_{1}$ ；

(2)、分别写出点 $A_{1} ， B_{1}$ 两点的坐标；

查看试题解析
19. “灰鸽子”是一种危害性很强的病毒，如果一台电脑不慎被感染“灰鸽子”病毒，经过两轮感染后就会 $289$ 台电脑被感染，请你用学过的知识分析，每轮感染中平均一台电脑会感染几台电脑？

查看试题解析
20. 请你依据如图框中的寻宝游戏规则，探究“寻宝游戏”的奥秘：

(1)、用树状图表示出所有可能的寻宝情况；

(2)、求在寻宝游戏中胜出的概率．

查看试题解析
21. 如图，在△ABC中，AB＝AC ， AD为BC边上的中线，DE⊥AB于点E ．

(1)、求证：△BDE∽△CAD；

(2)、若AB＝13，BC＝10，求线段DE的长．

查看试题解析
22. 如图，某小区①号楼与 11 号楼隔河相望，李明家住在①号楼，他很想知道 11 号楼的高度，于是他做了一些测量.他先在点测得点的仰角为60°，然后到42米高的楼顶 $A$ 处，测得点的仰角为30°，请你帮李明计算 11 号楼的高度 $C D$ .

查看试题解析
23. 如图，BD为△ABC外接圆⊙O的直径，且∠BAE=∠C．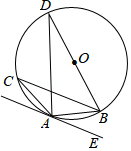

(1)、求证：AE与⊙O相切于点A；

(2)、若AE∥BC，BC=2 $\sqrt{7}$ ，AC=2 $\sqrt{2}$ ，求AD的长．

查看试题解析
24. 如图，在平面直角坐标系中，OA⊥OB，AB⊥x轴于点C，点A（ $\sqrt{3}$ ，1）在反比例函数 $y = \frac{k}{x}$ 的图象上．

(1)、求反比例函数 $y = \frac{k}{x}$ 的表达式；

(2)、在x轴的负半轴上存在一点P，使得S_△_AOP= S_△_AOB ，求点P的坐标；

(3)、若将△BOA绕点B按逆时针方向旋转60°得到△BDE．直接写出点E的坐标，并判断点E是否在该反比例函数的图象上，说明理由．

查看试题解析
25.
如图，△AEF中，∠EAF=45°，AG⊥EF于点G，现将△AEG沿AE折叠得到△AEB，将△AFG沿AF折叠得到△AFD，延长BE和DF相交于点C．

(1)、求证：四边形ABCD是正方形；

(2)、连接BD分别交AE、AF于点M、N，将△ABM绕点A逆时针旋转，使AB与AD重合，得到△ADH，试判断线段MN、ND、DH之间的数量关系，并说明理由．

(3)、若EG=4，GF=6，BM=3 $\sqrt{2}$ ，求AG、MN的长．

查看试题解析