广东省惠州市博罗县2018-2019学年中考数学一模考试试卷
试卷更新日期:2019-07-03 类型:中考模拟
一、单选题
-
1. 3的相反数是( )A、 B、3 C、﹣3 D、±2. 我国首艘国产航母于2018年4月26日正式下水,排水量约为65000吨,将65000用科学记数法表示为( )A、6.5×10﹣4 B、6.5×104 C、﹣6.5×104 D、65×1043. 二元一次方程组 的解是( )A、 B、 C、 D、4. 一个不透明的盒子中装有6个大小相同的乒乓球,其中4个是黄球,2个是白球.从该盒子中任意摸出一个球,摸到黄球的概率是( )A、 B、 C、 D、5. 下列图形既是轴对称图形,又是中心对称图形的是( )A、三角形 B、平行四边形 C、角 D、菱形6. 一个五边形的内角和为( )A、540° B、450° C、360° D、180°7. 如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则tanA的值为( )
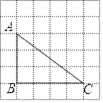 A、 B、 C、 D、8. 已知关于x的一元二次方程x2-2x+k-1=0有两个不相等的实数根,则实数 的取值范围是( )A、k≤2 B、k≤0 C、k<2 D、k<09. 如图,在△ABC中,点D、E分别是AB、AC的中点,若△ADE的面积为4,则△ABC的面积为( )
A、 B、 C、 D、8. 已知关于x的一元二次方程x2-2x+k-1=0有两个不相等的实数根,则实数 的取值范围是( )A、k≤2 B、k≤0 C、k<2 D、k<09. 如图,在△ABC中,点D、E分别是AB、AC的中点,若△ADE的面积为4,则△ABC的面积为( ) A、8 B、12 C、14 D、1610. 如图,已知A , B是反比例函数y= (k>0,x>0)图象上的两点,BC∥x轴,交y轴于点C , 动点P从坐标原点O出发,沿O→A→B→C(图中“→”所示路线)匀速运动,终点为C , 过P作PM⊥x轴,垂足为M . 设三角形OMP的面积为S , P点运动时间为t , 则S关于t的函数图象大致为( )
A、8 B、12 C、14 D、1610. 如图,已知A , B是反比例函数y= (k>0,x>0)图象上的两点,BC∥x轴,交y轴于点C , 动点P从坐标原点O出发,沿O→A→B→C(图中“→”所示路线)匀速运动,终点为C , 过P作PM⊥x轴,垂足为M . 设三角形OMP的面积为S , P点运动时间为t , 则S关于t的函数图象大致为( )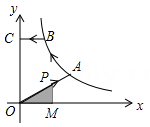 A、
A、 B、
B、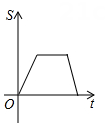 C、
C、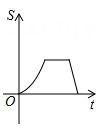 D、
D、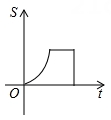
二、填空题
-
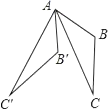
11. 不等式2x﹣6>0的解集是 .12. 分解因式:a2﹣9= .13. 已知点P(a,b)在反比例函数y= 的图象上,则ab= .14. 若m2﹣3m﹣1=0,则3m2﹣9m+2016的值为 .15. 如图所示,△ABC中,∠BAC=30°,将△ABC绕点A按顺时针方向旋转50°,对应得到△AB′C′,则∠B′AC的度数为 .
 16. 如图,正六边形ABCDEF的边长为1,以点A为圆心,AB的长为半径,作扇形ABF,则图中阴影部分的面积为(结果保留根号和π).
16. 如图,正六边形ABCDEF的边长为1,以点A为圆心,AB的长为半径,作扇形ABF,则图中阴影部分的面积为(结果保留根号和π).
三、解答题
-
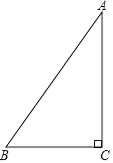
17. 计算: .18. 先化简,再求值: ,其中x=3.19. 如图,在Rt△ABC中,∠ACB=90°.
 (1)、请用直尺和圆规作∠ABC的平分线,交AC于点D(保留作图痕迹,不要求写作法和证明);(2)、在(1)作出的图形中,若∠A=30°,BC= ,则点D到AB的距离等于 .20. 近几年购物的支付方式日益增多,某数学兴趣小组就此进行了抽样调查.调查结果显示,支付方式有:A微信、B支付宝、C现金、D其他,该小组对某超市一天内购买者的支付方式进行调查统计,得到如下两幅不完整的统计图.
(1)、请用直尺和圆规作∠ABC的平分线,交AC于点D(保留作图痕迹,不要求写作法和证明);(2)、在(1)作出的图形中,若∠A=30°,BC= ,则点D到AB的距离等于 .20. 近几年购物的支付方式日益增多,某数学兴趣小组就此进行了抽样调查.调查结果显示,支付方式有:A微信、B支付宝、C现金、D其他,该小组对某超市一天内购买者的支付方式进行调查统计,得到如下两幅不完整的统计图.
请你根据统计图提供的信息,解答下列问题:
(1)、本次一共调查了多少名购买者?(2)、请补全条形统计图;在扇形统计图中A种支付方式所对应的圆心角为度.(3)、若该超市这一周内有1600名购买者,请你估计使用A和B两种支付方式的购买者共有多少名?21. 如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.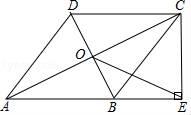 (1)、求证:四边形ABCD是菱形;(2)、若AB= ,BD=2,求OE的长.22. 某图书馆计划选购甲、乙两种图书.已知甲种图书每本价格是乙种图书每本价格的2.5倍,用800元单独购买甲种图书比用800元单独购买乙种图书要少24本.求:(1)、乙种图书每本价格为多少元?(2)、如果该图书馆计划购买乙种图书的本数比购买甲种图书本数的2倍多8本,且用于购买甲、乙两种图书的总经费不超过1060元,那么该图书馆最多可以购买多少本甲种图书?23. 如图,抛物线y=x2+bx﹣3过点A(1,0),直线AD交抛物线于点D , 点D的横坐标为﹣2,点P是线段AD上的动点.
(1)、求证:四边形ABCD是菱形;(2)、若AB= ,BD=2,求OE的长.22. 某图书馆计划选购甲、乙两种图书.已知甲种图书每本价格是乙种图书每本价格的2.5倍,用800元单独购买甲种图书比用800元单独购买乙种图书要少24本.求:(1)、乙种图书每本价格为多少元?(2)、如果该图书馆计划购买乙种图书的本数比购买甲种图书本数的2倍多8本,且用于购买甲、乙两种图书的总经费不超过1060元,那么该图书馆最多可以购买多少本甲种图书?23. 如图,抛物线y=x2+bx﹣3过点A(1,0),直线AD交抛物线于点D , 点D的横坐标为﹣2,点P是线段AD上的动点. (1)、b= , 抛物线的顶点坐标为;(2)、求直线AD的解析式;(3)、过点P的直线垂直于x轴,交抛物线于点Q , 连接AQ , DQ , 当△ADQ的面积等于△ABD的面积的一半时,求点Q的坐标.24. 如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,BD=BA , BE⊥DC交DC的延长线于点E .
(1)、b= , 抛物线的顶点坐标为;(2)、求直线AD的解析式;(3)、过点P的直线垂直于x轴,交抛物线于点Q , 连接AQ , DQ , 当△ADQ的面积等于△ABD的面积的一半时,求点Q的坐标.24. 如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,BD=BA , BE⊥DC交DC的延长线于点E . (1)、若∠BAD=70°,则∠BCA=°;(2)、若AB=12,BC=5,求DE的长:(3)、求证:BE是⊙O的切线.25. 有一块含30°角的直角三角板OMN , 其中∠MON=90°,∠NMO=30°,ON=2 ,将这块直角三角板按如图所示位置摆放.等边△ABC的顶点B与点O重合,BC边落在OM上,点A恰好落在斜边MN上,将等边△ABC从图1的位置沿OM方向以每秒1个单位长度的速度平移,边AB , AC分别与斜边MN交于点E , F(如图2所示),设△ABC平移的时间为t(s)(0<t<6).
(1)、若∠BAD=70°,则∠BCA=°;(2)、若AB=12,BC=5,求DE的长:(3)、求证:BE是⊙O的切线.25. 有一块含30°角的直角三角板OMN , 其中∠MON=90°,∠NMO=30°,ON=2 ,将这块直角三角板按如图所示位置摆放.等边△ABC的顶点B与点O重合,BC边落在OM上,点A恰好落在斜边MN上,将等边△ABC从图1的位置沿OM方向以每秒1个单位长度的速度平移,边AB , AC分别与斜边MN交于点E , F(如图2所示),设△ABC平移的时间为t(s)(0<t<6).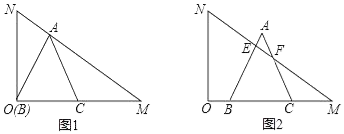 (1)、等边△ABC的边长为;(2)、在运动过程中,当时,MN垂直平分AB;(3)、当0<t<6时,求直角三角板OMN与等边△ABC重叠部分的面积S与时间t之间的函数关系式.
(1)、等边△ABC的边长为;(2)、在运动过程中,当时,MN垂直平分AB;(3)、当0<t<6时,求直角三角板OMN与等边△ABC重叠部分的面积S与时间t之间的函数关系式.