广东省广州市从化区2018-2019学年中考数学一模考试试卷
试卷更新日期:2019-07-03 类型:中考模拟
一、单选题
-
1. 6的相反数是( )A、 B、 C、 D、62. 如图,直线 ,直线 与直线 、 都相交, ,则 ( )
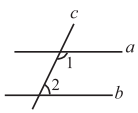 A、125° B、115° C、65° D、25°3. 下列式子计算正确的是( ).A、 B、 C、 D、4. 如图所示的几何体的左视图是( )
A、125° B、115° C、65° D、25°3. 下列式子计算正确的是( ).A、 B、 C、 D、4. 如图所示的几何体的左视图是( )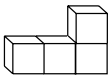 A、
A、 B、
B、 C、
C、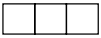 D、
D、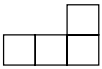 5. 若一组数据4,1,7,x,5的平均数为4,则这组数据的中位数为( )A、7 B、5 C、4 D、36. 已知 ,则 等于( )A、1 B、3 C、-1 D、-37. 将抛物线 向左平移1个单位,再向下平移3个单位得到的解析式是( ).A、 B、 C、 D、8. 如图,AB是⊙O的直径,MN是⊙O的切线,切点为N,如果∠MNB=52°,则∠NOA的度数为( )
5. 若一组数据4,1,7,x,5的平均数为4,则这组数据的中位数为( )A、7 B、5 C、4 D、36. 已知 ,则 等于( )A、1 B、3 C、-1 D、-37. 将抛物线 向左平移1个单位,再向下平移3个单位得到的解析式是( ).A、 B、 C、 D、8. 如图,AB是⊙O的直径,MN是⊙O的切线,切点为N,如果∠MNB=52°,则∠NOA的度数为( )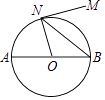 A、76° B、56° C、54° D、52°9. 已知二次函数 的图象如图所示,则下列说法正确的是( )
A、76° B、56° C、54° D、52°9. 已知二次函数 的图象如图所示,则下列说法正确的是( )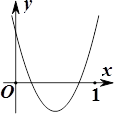 A、 <0 B、 <0 C、 <0 D、 <010. 如图,正方形 内接于圆 , ,则图中阴影部分的面积是( ).
A、 <0 B、 <0 C、 <0 D、 <010. 如图,正方形 内接于圆 , ,则图中阴影部分的面积是( ).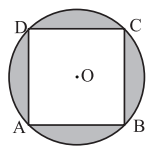 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 函数y= 中自变量x的取值范围为 .12. 截止到2018年5月31日,上海世博园共接待游客约8000000人,将数8000000用科学记数法表示为.13. 计算: = .14. 如图,已知菱形 , , ,则 .
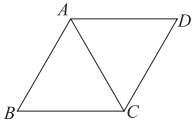 15. 阅读理解:引入新数 ,新数 满足分配律,结合律,交换律.已知 ,那么 .16. 在平面直角坐标系中,四边形AOBC为矩形,且点C坐标为(8,6),M为BC中点,反比例函数 (k是常数,k≠0) 的图象经过点M,交AC于点N,则MN的长度是.
15. 阅读理解:引入新数 ,新数 满足分配律,结合律,交换律.已知 ,那么 .16. 在平面直角坐标系中,四边形AOBC为矩形,且点C坐标为(8,6),M为BC中点,反比例函数 (k是常数,k≠0) 的图象经过点M,交AC于点N,则MN的长度是.
三、解答题
-
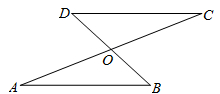
17. 解方程:18. 如图,AC和BD相交于点0,OA=OC, OB=OD.求证:DC//AB
 19. 已知代数式: .(1)、化简 ;(2)、已知 ,求 的值.20. 为了传承中华优秀传统文化,市教育局决定开展“经典诵读进校园”活动,某校团委组织八年级100名学生进行“经典诵读”选拔赛,赛后对全体参赛学生的成绩进行整理,得到下列不完整的统计图表.
19. 已知代数式: .(1)、化简 ;(2)、已知 ,求 的值.20. 为了传承中华优秀传统文化,市教育局决定开展“经典诵读进校园”活动,某校团委组织八年级100名学生进行“经典诵读”选拔赛,赛后对全体参赛学生的成绩进行整理,得到下列不完整的统计图表.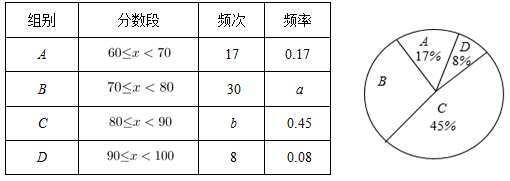
请根据所给信息,解答以下问题:
(1)、表中 ;(2)、请计算扇形统计图中B组对应扇形的圆心角的度数;(3)、已知有四名同学均取得98分的最好成绩,其中包括来自同一班级的甲、乙两名同学,学校将从这四名同学中随机选出两名参加市级比赛,请用列表法或画树状图法求甲、乙两名同学都被选中的概率.21. 如图,直线 与双曲线 相交于 , 两点,与 轴相交于点 . (1)、求 , 的值;(2)、若点 与点 关于 轴对称,求 的面积.22. 如图,某货船以24海里/时的速度将一批货物从 处运往正东方向的 处,在点 处测得某岛 在北偏东60°的方向上.该货船航行30分钟后到达 处,此时再测得该岛在北偏东30°的方向上,
(1)、求 , 的值;(2)、若点 与点 关于 轴对称,求 的面积.22. 如图,某货船以24海里/时的速度将一批货物从 处运往正东方向的 处,在点 处测得某岛 在北偏东60°的方向上.该货船航行30分钟后到达 处,此时再测得该岛在北偏东30°的方向上,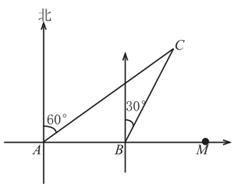 (1)、求 的度数;(2)、已知在 岛周围9海里的区域内有暗礁.若继续向正东方向航行,该货船有无触礁危险?试说明理由.(参考: 、 )23. 如图,在△ABC 中,∠C=90°
(1)、求 的度数;(2)、已知在 岛周围9海里的区域内有暗礁.若继续向正东方向航行,该货船有无触礁危险?试说明理由.(参考: 、 )23. 如图,在△ABC 中,∠C=90°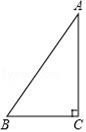 (1)、利用尺规作∠B 的角平分线交AC于D,以BD为直径作⊙O交AB于E(保留作图痕迹,不写作法);(2)、综合应用:在(1)的条件下,连接DE
(1)、利用尺规作∠B 的角平分线交AC于D,以BD为直径作⊙O交AB于E(保留作图痕迹,不写作法);(2)、综合应用:在(1)的条件下,连接DE①求证:CD=DE;
②若sinA= ,AC=6,求AD.
24. 如图, 是半圆 的直径, 是 延长线上的点, 的垂直平分线交半圆于点 ,交 于点 ,连接 , .已知半圆 的半径为3, .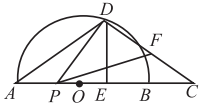 (1)、求 的长.(2)、点 是线段 上一动点,连接 ,作 , 交线段 于点 .当 为等腰三角形时,求 的长.25. 在平面直角坐标系中,二次函数y=ax2+ x+c的图象经过点C(0,2)和点D(4,﹣2).点E是直线y=﹣ x+2与二次函数图象在第一象限内的交点.
(1)、求 的长.(2)、点 是线段 上一动点,连接 ,作 , 交线段 于点 .当 为等腰三角形时,求 的长.25. 在平面直角坐标系中,二次函数y=ax2+ x+c的图象经过点C(0,2)和点D(4,﹣2).点E是直线y=﹣ x+2与二次函数图象在第一象限内的交点.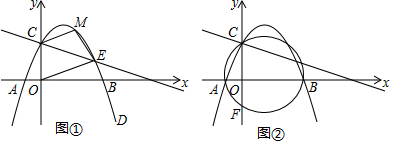 (1)、求二次函数的解析式及点E的坐标.(2)、如图①,若点M是二次函数图象上的点,且在直线CE的上方,连接MC,OE,ME.求四边形COEM面积的最大值及此时点M的坐标.(3)、如图②,经过A、B、C三点的圆交y轴于点F,求点F的坐标.
(1)、求二次函数的解析式及点E的坐标.(2)、如图①,若点M是二次函数图象上的点,且在直线CE的上方,连接MC,OE,ME.求四边形COEM面积的最大值及此时点M的坐标.(3)、如图②,经过A、B、C三点的圆交y轴于点F,求点F的坐标.