广东省广州市白云区2018-2019学年中考数学一模考试试卷

试卷更新日期：2019-07-03 类型：中考模拟

进入出卷网下载

一、单选题

1. 2的相反数是（）

A、﹣2 B、 $\frac{1}{2}$ C、﹣ $\frac{1}{2}$ D、2

查看试题解析
2. 式子 $\sqrt{x - 1}$ 在实数范围内有意义，那么（）

A、 $x > - 1$ B、 $x > 1$ C、 $x \geq - 1$ D、 $x \geq 1$

查看试题解析
3. 如图所示的几何体主视图是（）

A、 B、 C、 D、

查看试题解析
4. 下列计算中，正确的是（）

A、 $a + 2 a = 3 a^{2}$ B、 $3 a - 2 a = a$ C、 $a \cdot 2 a = 3 a^{2}$ D、 $2 (a + 1) = 2 a$

查看试题解析
5. 若一组数据为：2，3，1，3，3．则下列说法错误的是（）

A、这组数据的众数是3 B、事件“在这组数据中随机抽取1个数，抽到的数是 $0.$ “是不可能事件 C、这组数据的中位数是3 D、这组数据的平均数是3

查看试题解析
6. 下列各实数中，最接近3的是（）

A、 $\sqrt{2}$ B、 $\sqrt{6}$ C、 $\sqrt{10}$ D、 $\sqrt{12}$

查看试题解析
7. 在数轴上用点B表示实数b ．若关于x的一元二次方程x²+bx+1=0有两个相等的实数根，则（）

A、 $O B = 2$ B、 $O B > 2$ C、 $O B \geq 2$ D、 $O B < 2$

查看试题解析
8. 画△ABC ，使∠A=45°，AB=10cm ， ∠A的对边只能在长度分别为6cm、7cm、8cm、9cm的四条线段中任选，可画出（）个不同形状的三角形．

A、2 B、3 C、4 D、6

查看试题解析
9. 若一次函数y=kx+b的图象如图所示，则下列结论中，正确的有（）
①二次函数y=x²+kx+b的图象一定经过点(0，2)；②二次函数y=x²+kx+b的图象开口向上；③二次函数y=x²+kx+b的图象对称轴在y轴左侧；④二次函数y=x²+kx+b的图象不经过第二象限.

A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 如图，过△ABC内任一点P ，作DE∥BC ， GF∥AC ， KH∥AB ，则 $\frac{D E}{B C} + \frac{G F}{A C} + \frac{K H}{A B}$ =（）

A、1 B、 $\frac{4}{3}$ C、2 D、 $\frac{8}{3}$

查看试题解析

二、填空题

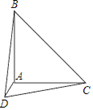
11. 已知∠1=23°，则∠1的余角是°．

查看试题解析
12. 白云湖是广州市政府便民利民的综合性水利工程，北部水系首期工程完工后，每天可以从珠江西航道引入1000000万立方米的活水进入白云湖，进而改善周边河涌的水质．将1000000用科学记数法可记为．

查看试题解析
13. 分解因式：2ab²-6a²= ．

查看试题解析
14. 把二次函数y=x²+2x+3的图象向左平移1个单位长度，再向下平移1个单位长度，就得到二次函数的图象．

查看试题解析
15. 3张除所标数值外完全相同的卡片，它们标有的数值分别为1、2、-3．把这3张卡片，背面朝上放在桌面上，随机抽取2张，把抽到卡片上的数值分别作为A点的横坐标、纵坐标，则A点落在第一象限的概率是．

查看试题解析
16. 如图，AB=AC ， ∠CAB=90°，∠ADC=45°，AD=1，CD=3，则BD= ．

查看试题解析

三、解答题

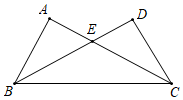
17. 解下列不等式，并在数轴上表示解集：2（x-3）＞1．

查看试题解析
18. 如图，已知AB=DC ， ∠ABC=∠DCB ， E为AC、BD的交点．求证：AC=DB ．

查看试题解析
19. 已知A=（3x-1）（2x+1）-x+1-6y² ．

(1)、化简A；

(2)、当x、y满足方程组 ${\begin{matrix} x + y = 5 \\ x - y = 1 \end{matrix}$ 时，求A的值．

查看试题解析
20. 从某校1500名学生中随机抽查了40名学生对球类运动的喜好情况．整理数据后绘制成扇形统计图，如图：

(1)、直接写出被抽查的40名学生中，“最喜欢篮球”的人数人，“最喜欢乒乓球”对应扇形的圆心角度数；根据调查结果可估计该校学生中“最喜欢足球”的人数约为．

(2)、在被抽查的40名学生中，“最喜欢篮球”的调查结果：只有2名女生，其余的都是男生．现从上述所有“最喜欢篮球”的学生中随机抽取2名学生进行篮球技能测试，求所抽取的2名学生中至少有1名女生的概率．

查看试题解析
21. 如图，一次函数y=kx+b与反比例函数y= $\frac{m}{x}$ 的图象交于A（n ， 3），B（-3，-2）两点．

(1)、求反比例函数与一次函数的解析式；

(2)、过点B作BC⊥x轴，垂足为C ，求S_△_ABC ．

查看试题解析
22. 开学初，某文化用品商店减价促销，全场8折．购买规格相同的铅笔套装，折价后用32元买到的数量刚好比按原价用50元买到的数量少2套．求原来每套铅笔套装的价格是多少元？

查看试题解析
23. 已知：如图，在矩形ABCD中，E为AD的中点，连结EC（AB＞AE）．

(1)、尺规作图：过点E作EF⊥EC交AB于F点，连结FC；（保留作图痕迹，不要求写作法和证明）

(2)、在（1）所作的图中，求证：△AEF∽△ECF ．

(3)、在（1）所作的图中，∠BCF≠∠AFE ，设 $\frac{A B}{B C}$ =k ，是否存在这样的k值，使得△AEF与△BFC相似？若存在，证明你的结论并求出k的值；若不存在，说明理由．

查看试题解析
24. 如图，已知二次函数 $y = \frac{1}{2} x^{2} + b x + c$ 的图象经过点A（-3，6），并与x轴交于点B（-1，0）和点C ，顶点为点P ．

(1)、求这个二次函数解析式；

(2)、设D为x轴上一点，满足∠DPC=∠BAC ，求点D的坐标；

(3)、作直线AP ，在抛物线的对称轴上是否存在一点M ，在直线AP上是否存在点N ，使AM+MN的值最小？若存在，求出M、N的坐标：若不存在，请说明理由．

查看试题解析
25. 如图①，已知△ABC内接于⊙O ， ∠BOC=120°，点A在优弧BC上运动，点M是 $\overset{�}{A C}$ 的中点，BM交AC于点D ，点N是 $\overset{�}{A B}$ 的中点，CN交AB于点E ， B
D、CE相交于点F ．

(1)、求证：当∠ACB=60°时，如图②，点F与点O重合；

(2)、求证：EF=DF；

(3)、在（1）中，若△ABC的边长为2，将△ABD绕点D ，按逆时针方向旋转m°，得到△HGD（DH＜DG），AB与DH交于点J ， DG与CN交于点I ，当0＜m＜60时，△DLJ的面积S是否改变？如果不变，求S的值；如果改变，求S的取值范围．

查看试题解析