广东省佛山市顺德区2018-2019学年中考数学三模考试试卷

试卷更新日期：2019-07-03 类型：中考模拟

进入出卷网下载

一、单选题

1. |﹣2019|等于（）

A、2019 B、﹣2019 C、 $\frac{1}{2019}$ D、﹣ $\frac{1}{2019}$

查看试题解析
2. 0.0021用科学记数法表示为（）

A、2.1×10^﹣² B、2.1×10^﹣³ C、2.1×10^﹣⁴ D、21×10^﹣²

查看试题解析
3. 展开图可能是如图的几何体是（）

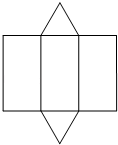A、三棱柱 B、圆柱 C、四棱柱 D、圆锥

查看试题解析
4. 在平面直角坐标系中，点（﹣2，3）所在的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
5. 下列运算正确的是（）

A、3a﹣a＝3 B、a⁶÷a²＝a³ C、﹣a（1﹣a）＝﹣a+a² D、 ${(\frac{1}{2})}^{- 2} = - 2$

查看试题解析
6. 如图，对菱形ABCD的叙述正确的是（）

A、AC＝BD B、∠OAB＝∠OBA C、AC⊥BD D、有4条对称轴

查看试题解析
7. 如图，直线a∥b，∠2＝35°，∠3＝40°，则∠1的度数是（）

A、75° B、105° C、140° D、145°

查看试题解析
8. 如图，二次函数y＝ax²+bx+c图象的对称轴是直线x＝1，与x轴一个交点A（3，0），则与x轴的另一个交点坐标是（）

A、（0， $- \frac{1}{2}$ ） B、（ $- \frac{1}{2}$ ，0） C、（0，﹣1） D、（﹣1，0）

查看试题解析
9. 在一次捐书活动中，A、B、C、D分别表示“名人传记”、“科普图书”、“小说”、“其它图书”某校九年级学生捐书情况如下：

图书种类

A

B

C

D

数目（本）

A

175

100

d

下列哪个选项是错误的（）

A、共捐书500本 B、a＝150 C、“C”所占的百分比是20% D、“扇形D”的圆心角是50°

查看试题解析
10. 如图，在△ABC中，AC＝BC，∠C＝90°，折叠△ABC使得点C落在AB边上的E处，连接DE、CE，下列结论：①△DEB是等腰直角三角形；②AB＝AC+CD；③ $\frac{BE}{AC} = \frac{BD}{AB}$ ；④S_△_CDE＝S_△_BDE ．其中符合题意的个数是（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11. 因式分解：x²﹣x= ．

查看试题解析
12. $\frac{8}{27}$ 的立方根是．

查看试题解析
13. 计算：18°30′＝°．

查看试题解析
14. 在Rt△ABC中，∠C＝90°，AC＝3，BC＝4，点D、E、F是三边的中点，则△DEF的周长是．

查看试题解析
15. 方程 $\frac{480}{x} - \frac{600}{2 x}$ ＝45的解是．

查看试题解析
16. 如图，⊙O的半径为4，点P到圆心的距离为8，过点P画⊙O的两条切线PA和PB，A，B为切点，则阴影部分的面积是．（结果保留π）

查看试题解析

三、解答题

17. 解不等式： $\frac{x - 2}{2} < \frac{7 - x}{3}$

查看试题解析
18. 先化简，再求值 $\frac{a^{2} - 4}{a^{2} + 4 a + 4} - \frac{a}{a + 2}$ ，其中a＝ $\sqrt{2}$ ﹣2．

查看试题解析
19. 如图，在△ABC中，AB＝AC．

(1)、用尺规作图法在AC边上找一点D，使得BD＝BC（保留作图痕迹，不要求写作法）：

(2)、若∠A＝30°，求∠ABD的大小．

查看试题解析
20. 甲、乙两名同学参加少年科技创新选拔赛，六次比赛的成绩如下：
甲：87 93 88 93 89 90

乙：85 90 90 96 89 a

(1)、甲同学成绩的中位数是；

(2)、若甲、乙的平均成绩相同，则a＝；

(3)、已知乙的方差是 $\frac{31}{2}$ ，如果要选派一名发挥稳定的同学参加比赛，应该选谁？说明理由．（方差公式：S²＝ $\frac{{(x_{1} - x)}^{2} + {(x_{2} - x)}^{2} + {(x_{3} - x)}^{2} + \dots + {(x_{n} - x)}^{2}}{n})$

查看试题解析
21. 某单位需要购买一些钢笔和笔记本．若购买2支钢笔和1本笔记本需42元，购买3支钢笔和2本笔记本需68元．

(1)、求买一支钢笔要多少钱？

(2)、若购买了钢笔和笔记本共50件，付款可能是810元吗？说明理由．

查看试题解析
22. 如图，点E在矩形ABCD的边AD上，且∠EBC＝∠ECB．

(1)、求证：AE＝ED；

(2)、连接BD交CB于点F，求△BCF和△DEF的面积之比．

查看试题解析
23. 如图，反比例函数y＝ $\frac{2}{x}$ 的图象和一次函数的图象交于A、B两点，点A的横坐标和点B的纵坐标都是1．

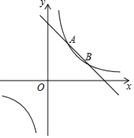(1)、在第一象限内，写出关于x的不等式kx+b≥ $\frac{2}{x}$ 的解集；

(2)、求一次函数的表达式；

(3)、若点P（m，n）在反比例函数图象上，且关于y轴对称的点Q恰好落在一次函数的图象上，求m²+n²的值．

查看试题解析
24. 如图，点C是等边△ABD的边AD上的一点，且∠ACB＝75°，⊙O是△ABC的外接圆，连结AO并延长交BD于E、交⊙O于F．

(1)、求证：∠BAF＝∠CBD；

(2)、过点C作CG∥AE交BD于点G，求证：CG是⊙O的切线；

(3)、在（2）的条件下，当AF＝2 $\sqrt{2}$ 时，求 $\frac{DG}{AC}$ 的值．

查看试题解析
25. 如图，点O是平面直角坐标系的原点，点A（ $\sqrt{3}$ ，3），AC⊥OA与x轴的交点为C．动点M以每秒 $\sqrt{3}$ 个单位长度由点A向点O运动．同时，动点N以每秒3个单位长度由点O向点C运动，当一动点先到终点时，另一动点立即停止运动．

(1)、写出∠AOC的值；

(2)、用t表示出四边形AMNC的面积；

(3)、求点P的坐标，使得以O、N、M、P为顶点的四边形是特殊的平行四边形？

查看试题解析

图书种类	A	B	C	D
数目（本）	A	175	100	d