广东省湛江市霞山区2018-2019学年中考数学一模考试试卷
试卷更新日期:2019-07-03 类型:中考模拟
一、单选题
-
1. 在2,﹣3,0,﹣ 这四个数中,最大的是( )A、2 B、﹣3 C、0 D、﹣2. 港珠澳大桥目前是全世界最长的跨海大桥,其主体工程“海中桥隧”全长35578米,数据35578用科学记数法表示为( )A、35.578×103 B、3.5578×104 C、3.5578×105 D、0.35578×1053. 9的算术平方根是( )A、±3 B、3 C、± D、4. 下列图形中是轴对称图形但不是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 5. 如果一个角的余角是50°,那么这个角的度数是( )A、30° B、40° C、50° D、130°6. 已知一元二次方程ax2+ax﹣4=0有一个根是﹣2,则a值是( )A、﹣2 B、 C、2 D、47. 如图,点P是∠AOB的角平分线OC上一点,PD⊥OA,垂足为点D,PD=2,M为OP的中点,则点M到射线OB的距离为( )
5. 如果一个角的余角是50°,那么这个角的度数是( )A、30° B、40° C、50° D、130°6. 已知一元二次方程ax2+ax﹣4=0有一个根是﹣2,则a值是( )A、﹣2 B、 C、2 D、47. 如图,点P是∠AOB的角平分线OC上一点,PD⊥OA,垂足为点D,PD=2,M为OP的中点,则点M到射线OB的距离为( )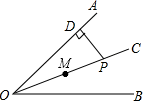 A、 B、1 C、 D、28. 下列判断错误的是( )A、两组对边分别相等的四边形是平行四边形 B、四个内角都相等的四边形是矩形 C、两条对角线垂直且平分的四边形是正方形 D、四条边都相等的四边形是菱形9. 已知反比例函数 ,下列结论中错误的是( )A、图象经过点(﹣1,﹣2) B、图象在第一、三象限 C、当x>1时,0<y<2 D、当x<0时,y随着x的增大而增大10. 如图,在正方形ABCD中,AB= ,P为对角线AC上的动点,PQ⊥AC交折线A﹣D﹣C于点Q,设AP=x,△APQ的面积为y,则y与x的函数图象正确的是( )
A、 B、1 C、 D、28. 下列判断错误的是( )A、两组对边分别相等的四边形是平行四边形 B、四个内角都相等的四边形是矩形 C、两条对角线垂直且平分的四边形是正方形 D、四条边都相等的四边形是菱形9. 已知反比例函数 ,下列结论中错误的是( )A、图象经过点(﹣1,﹣2) B、图象在第一、三象限 C、当x>1时,0<y<2 D、当x<0时,y随着x的增大而增大10. 如图,在正方形ABCD中,AB= ,P为对角线AC上的动点,PQ⊥AC交折线A﹣D﹣C于点Q,设AP=x,△APQ的面积为y,则y与x的函数图象正确的是( )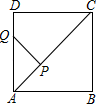 A、
A、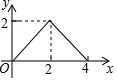 B、
B、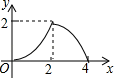 C、
C、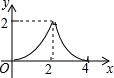 D、
D、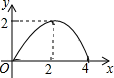
二、填空题
-
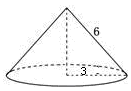
11. 分解因式:x3﹣x= .12. 从1、2、3、4这四个数中任取两个不同的数相乘,积为偶数的概率是 .13. 一个多边形的内角和是外角和的2倍,则这个多边形的边数为 .14. 分式方程 的解是 .15. 如图,圆锥的底面半径为3cm,母线长为6cm,那么这个圆锥的侧面积是cm2(结果保留π).
 16. 如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,……,依次进行下去,若点A( ,0),B(0,2),则点B2019的坐标为 .
16. 如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,……,依次进行下去,若点A( ,0),B(0,2),则点B2019的坐标为 .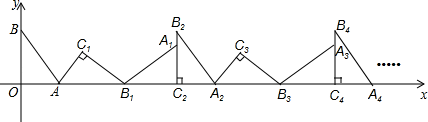
三、解答题
-
17. 计算: .18. 先化简,再求值: ,其中 .19. 如图,△ABC中,AB=AC,∠A=40°
 (1)、作边AB的垂直平分线MN,交AC于点D.(保留作图痕迹,不写作法)(2)、连结BD,求∠DBC的度数.20. 某年级共有300名学生.为了解该年级学生A,B两门课程的学习情况,从中随机抽取60名学生进行测试,获得了他们的成绩(百分制),并对数据(成绩)进行整理、描述和分析.下面给出了部分信息.
(1)、作边AB的垂直平分线MN,交AC于点D.(保留作图痕迹,不写作法)(2)、连结BD,求∠DBC的度数.20. 某年级共有300名学生.为了解该年级学生A,B两门课程的学习情况,从中随机抽取60名学生进行测试,获得了他们的成绩(百分制),并对数据(成绩)进行整理、描述和分析.下面给出了部分信息..A课程成绩的频数分布直方图如下(数据分成6组: , , , , , );
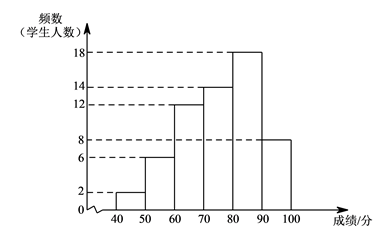
.A课程成绩在 这一组是:
70 71 71 71 76 76 77 78 79 79 79
.A,B两门课程成绩的平均数、中位数、众数如下:
课程
平均数
中位数
众数
A
B
70
83
根据以上信息,回答下列问题:
(1)、写出表中 的值;(2)、在此次测试中,某学生的A课程成绩为76分,B课程成绩为71分,这名学生成绩排名更靠前的课程是(填“A”或“B”),理由是;(3)、假设该年级学生都参加此次测试,估计A课程成绩超过 分的人数.21. 如图1,已知点A,B,C,D在一条直线上,BF、CE相交于O,AE=DF,∠E=∠F,OB=OC.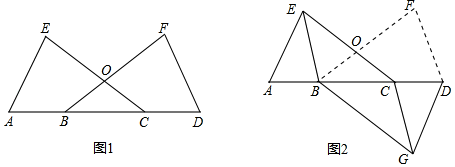 (1)、求证:△ACE≌△DBF;(2)、如果把△DBF沿AD折翻折使点F落在点G,如图2,连接BE和CG. 求证:四边形BGCE是平行四边形.22. 某学校为了改善办学条件,计划购置一批电子白板和台式电脑.经招投标,购买一台电子白板比购买2台台式电脑多3000元,购买2台电子白板和3台台式电脑共需2.7万元.(1)、求购买一台电子白板和一台台式电脑各需多少元?(2)、根据该校实际情况,购买电子白板和台式电脑的总台数为24,并且台式电脑的台数不超过电子白板台数的3倍.问怎样购买最省钱?23. 如图,抛物线y=x2+bx+c与x轴相交于A(﹣1,0),B(3,0),于y轴交于C.
(1)、求证:△ACE≌△DBF;(2)、如果把△DBF沿AD折翻折使点F落在点G,如图2,连接BE和CG. 求证:四边形BGCE是平行四边形.22. 某学校为了改善办学条件,计划购置一批电子白板和台式电脑.经招投标,购买一台电子白板比购买2台台式电脑多3000元,购买2台电子白板和3台台式电脑共需2.7万元.(1)、求购买一台电子白板和一台台式电脑各需多少元?(2)、根据该校实际情况,购买电子白板和台式电脑的总台数为24,并且台式电脑的台数不超过电子白板台数的3倍.问怎样购买最省钱?23. 如图,抛物线y=x2+bx+c与x轴相交于A(﹣1,0),B(3,0),于y轴交于C.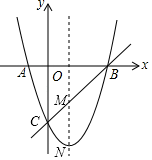 (1)、求该抛物线的解析式;(2)、若M是抛物线的对称轴与直线BC的交点,N是抛物线的顶点,求MN的长;(3)、若点P是抛物线上点,当S△PAB=8时,求点P的坐标.24. 如图,四边形ABCD的顶点在⊙O上,BD是⊙O的直径,延长CD、BA交于点E , 连接AC、BD交于点F , 作AH⊥CE , 垂足为点H , 已知∠ADE=∠ACB .
(1)、求该抛物线的解析式;(2)、若M是抛物线的对称轴与直线BC的交点,N是抛物线的顶点,求MN的长;(3)、若点P是抛物线上点,当S△PAB=8时,求点P的坐标.24. 如图,四边形ABCD的顶点在⊙O上,BD是⊙O的直径,延长CD、BA交于点E , 连接AC、BD交于点F , 作AH⊥CE , 垂足为点H , 已知∠ADE=∠ACB .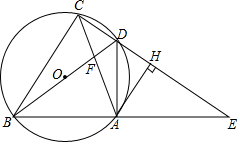 (1)、求证:AH是⊙O的切线;(2)、若OB=4,AC=6,求sin∠ACB的值;(3)、若 ,求证:CD=DH .25. 如图,在平面直角坐标系中,矩形OABC的顶点B坐标为(4,6),点P为线段OA上一动点(与点O、A不重合),连接CP,过点P作PE⊥CP交AB于点D,且PE=PC,过点P作PF⊥OP且PF=PO(点F在第一象限),连结FD、BE、BF,设OP=t.
(1)、求证:AH是⊙O的切线;(2)、若OB=4,AC=6,求sin∠ACB的值;(3)、若 ,求证:CD=DH .25. 如图,在平面直角坐标系中,矩形OABC的顶点B坐标为(4,6),点P为线段OA上一动点(与点O、A不重合),连接CP,过点P作PE⊥CP交AB于点D,且PE=PC,过点P作PF⊥OP且PF=PO(点F在第一象限),连结FD、BE、BF,设OP=t.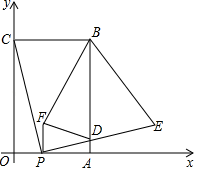 (1)、直接写出点E的坐标(用含t的代数式表示):;(2)、四边形BFDE的面积记为S,当t为何值时,S有最小值,并求出最小值;(3)、△BDF能否是等腰直角三角形,若能,求出t;若不能,说明理由.
(1)、直接写出点E的坐标(用含t的代数式表示):;(2)、四边形BFDE的面积记为S,当t为何值时,S有最小值,并求出最小值;(3)、△BDF能否是等腰直角三角形,若能,求出t;若不能,说明理由.