广东省梅州市大埔县茶阳片区2018-2019学年中考数学模拟考试试卷
试卷更新日期:2019-07-03 类型:中考模拟
一、单选题
-
1. 如果向东走 记为 ,则向西走 可记为( )A、 B、 C、 D、2. 函数y= 中,自变量x的取值范围为( )A、x> B、x≠ C、x≠ 且x≠0 D、x<3. 据报道,目前我国“天河二号”超级计算机的运算速度位居全球第一,其运算速度达到了每秒338 600 000亿次,数字338 600 000用科学记数法可简洁表示为( )A、3.386×108 B、0.3386×109 C、33.86×107 D、3.386×1094. 如图是由三个相同小正方体组成的几何体的主视图,那么这个几何体可以是( )
 A、
A、 B、
B、 C、
C、 D、
D、 5. 下列运算正确的是( )A、8a﹣a=8 B、(﹣a)4=a4 C、a3•a2=a6 D、(a﹣b)2=a2﹣b26. 在平面直角坐标系中,若点A(a,-b)在第一象限内,则点B(a,b)所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 如图,在▱ABCD中,M是BC延长线上的一点,若∠A=135°,则∠MCD的度数是( )
5. 下列运算正确的是( )A、8a﹣a=8 B、(﹣a)4=a4 C、a3•a2=a6 D、(a﹣b)2=a2﹣b26. 在平面直角坐标系中,若点A(a,-b)在第一象限内,则点B(a,b)所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 如图,在▱ABCD中,M是BC延长线上的一点,若∠A=135°,则∠MCD的度数是( )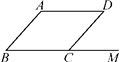 A、45° B、55° C、65° D、75°8. 若方程3 -4x-4=0的两个实数根分别为 , ,则 =( )A、-4 B、3 C、− D、9. 若 =1,则 -1+x的值为( )A、0 B、2 C、3 D、410. 如图,直线y1=x+b与y2=kx﹣1相交于点P , 点P的横坐标为﹣1,则关于x的不等式x+b>kx﹣1的解集在数轴上表示正确的是( )
A、45° B、55° C、65° D、75°8. 若方程3 -4x-4=0的两个实数根分别为 , ,则 =( )A、-4 B、3 C、− D、9. 若 =1,则 -1+x的值为( )A、0 B、2 C、3 D、410. 如图,直线y1=x+b与y2=kx﹣1相交于点P , 点P的横坐标为﹣1,则关于x的不等式x+b>kx﹣1的解集在数轴上表示正确的是( ) A、
A、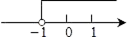 B、
B、 C、
C、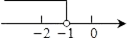 D、
D、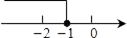
二、填空题
-
11. 已知x2+2x﹣1=0,则3x2+6x﹣2= .12. 在一个不透明的口袋中,装有A,B,C,D4个完全相同的小球,随机摸取一个小球然后放回,再随机摸取一个小球,两次摸到同一个小球的概率是 .13. 在实数范围内分解因式:x3﹣2x= .14. 用一个圆心角为180°,半径为4的扇形围成一个圆锥的侧面,则这个圆锥的底面圆的半径为 .15. 用反证法证明:“三角形中至少有两个锐角”时,首先应假设这个三角形中 .16. 如图,在Rt△ABC中,∠B=90°,AB=BC=2,将△ABC绕点C顺时针旋转60°,得到△DEC,则AE的长是 .

三、解答题
-
17. 计算: .18. 解方程: .19. 如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,1),B(0,3),C(0,1).
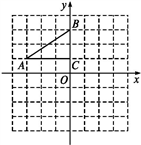 (1)、将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;(2)、分别连接AB1 , BA1后,求四边形AB1A1B的面积.20. 如图,在▱ABCD中,点E,F在对角线AC上,且AE=CF.求证:
(1)、将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;(2)、分别连接AB1 , BA1后,求四边形AB1A1B的面积.20. 如图,在▱ABCD中,点E,F在对角线AC上,且AE=CF.求证: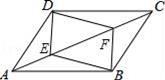 (1)、DE=BF;(2)、四边形DEBF是平行四边形.21. 我市某中学决定在学生中开展丢沙包、打篮球、跳大绳和踢毽球四种项目的活动,为了解学生对四种项目的喜欢情况,随机调查了该校m名学生最喜欢的一种项目(每名学生必选且只能选择四种活动项目的一种),并将调查结果绘制成如下的不完整的统计图表:
(1)、DE=BF;(2)、四边形DEBF是平行四边形.21. 我市某中学决定在学生中开展丢沙包、打篮球、跳大绳和踢毽球四种项目的活动,为了解学生对四种项目的喜欢情况,随机调查了该校m名学生最喜欢的一种项目(每名学生必选且只能选择四种活动项目的一种),并将调查结果绘制成如下的不完整的统计图表:学生最喜欢的活动项目的人数统计表
项目
学生数(名)
百分比
丢沙包
20
10%
打篮球
60
p%
跳大绳
n
40%
踢毽球
40
20%
根据图表中提供的信息,解答下列问题
(1)、m= , n= , p= .(2)、请根据以上信息直接补全条形统计图;(3)、根据抽样调查结果,请你估计该校2000名学生中有多少名学生最喜欢跳大绳学生最喜欢的活动项目的人数条形统计图.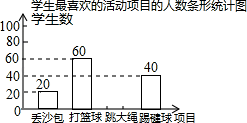 22. 如图所示,飞机在一定高度上沿水平直线飞行,先在点 处测得正前方小岛 的俯角为 ,面向小岛方向继续飞行 到达 处,发现小岛在其正后方,此时测得小岛的俯角为 .如果小岛高度忽略不计,求飞机飞行的高度(结果保留根号).
22. 如图所示,飞机在一定高度上沿水平直线飞行,先在点 处测得正前方小岛 的俯角为 ,面向小岛方向继续飞行 到达 处,发现小岛在其正后方,此时测得小岛的俯角为 .如果小岛高度忽略不计,求飞机飞行的高度(结果保留根号).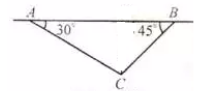 23. 如图,一次函数y=ax﹣1的图象与反比例函数 的图象交于A,B两点,与x轴交于点C,与y轴交于点D,已知OA= ,tan∠AOC=
23. 如图,一次函数y=ax﹣1的图象与反比例函数 的图象交于A,B两点,与x轴交于点C,与y轴交于点D,已知OA= ,tan∠AOC=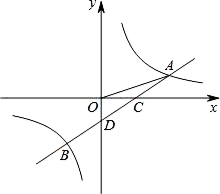 (1)、求a,k的值及点B的坐标;(2)、观察图象,请直接写出不等式ax﹣1≥ 的解集;(3)、在y轴上存在一点P,使得△PDC与△ODC相似,请你求出P点的坐标.24. 如图,在△ABC中,AB=AC,点D在BC上,BD=DC,过点D作DE⊥AC,垂足为E,⊙O经过A,B,D三点.
(1)、求a,k的值及点B的坐标;(2)、观察图象,请直接写出不等式ax﹣1≥ 的解集;(3)、在y轴上存在一点P,使得△PDC与△ODC相似,请你求出P点的坐标.24. 如图,在△ABC中,AB=AC,点D在BC上,BD=DC,过点D作DE⊥AC,垂足为E,⊙O经过A,B,D三点.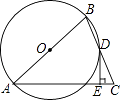 (1)、求证:AB是⊙O的直径;
(1)、求证:AB是⊙O的直径;
(2)、判断DE与⊙O的位置关系,并加以证明;
(3)、若⊙O的半径为3,∠BAC=60°,求DE的长.25. 如图,在平面直角坐标系中,四边形OABC为菱形,点C的坐标为(4,0),∠AOC=60°,垂直于x轴的直线l从y轴出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线l与菱形OABC的两边分别交于点M、N(点M在点N的上方).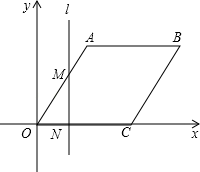 (1)、求A、B两点的坐标;(2)、设△OMN的面积为S , 直线l运动时间为t秒(0≤t≤6),试求S与t的函数表达式;(3)、在题(2)的条件下,是否存在某一时刻,使得△OMN的面积与OABC的面积之比为3:4?如果存在,请求出t的取值;如果不存在,请说明理由.
(1)、求A、B两点的坐标;(2)、设△OMN的面积为S , 直线l运动时间为t秒(0≤t≤6),试求S与t的函数表达式;(3)、在题(2)的条件下,是否存在某一时刻,使得△OMN的面积与OABC的面积之比为3:4?如果存在,请求出t的取值;如果不存在,请说明理由.