吉林省长春市2019年中考数学考试试卷
试卷更新日期:2019-07-02 类型:中考真卷
一、选择题(本大题共8小题,每小题3分,共24分)
-
1. 如图,数轴上表示-2的点A到原点的距离是( )

A、-2. B、2. C、 D、2. 2019年春运前四日,全国铁路、道路、水路、民航共累计发送旅客约为275 000 000人次,275 000 000这个数用科学记数法表示为( )A、27.5×107 B、0.275×109 C、2.75×108 D、2.75×1093. 如图是由4个相同的小正方体组成的立体图形,这个立体图形的主视图是( )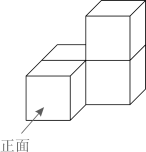 A、
A、 B、
B、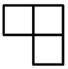 C、
C、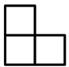 D、
D、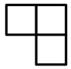 4. 不等式-x+2≥0的解集为( )A、x≥-2. B、 x≤-2 C、x≥2 D、x≤25. 《九章算术》是中国古代重要的数学著作。其中“盈不足术”记载:今有共买鸡,人出九,盈十一;人出六,不足十六。问人数鸡价各几何?译文:今有人合伙买鸡,每人出9钱,会多出11钱;每人出6钱,又差16钱。问人数、买鸡的钱数各是多少?设人数为x,买鸡的钱数为y,可列方程组为( )A、 B、 C、 D、6. 如图,一把梯子靠在垂直水平地面的墙上,梯子AB的长是3米。若梯子与地面的夹角为α,则梯子顶端到地面的距离BC为( )
4. 不等式-x+2≥0的解集为( )A、x≥-2. B、 x≤-2 C、x≥2 D、x≤25. 《九章算术》是中国古代重要的数学著作。其中“盈不足术”记载:今有共买鸡,人出九,盈十一;人出六,不足十六。问人数鸡价各几何?译文:今有人合伙买鸡,每人出9钱,会多出11钱;每人出6钱,又差16钱。问人数、买鸡的钱数各是多少?设人数为x,买鸡的钱数为y,可列方程组为( )A、 B、 C、 D、6. 如图,一把梯子靠在垂直水平地面的墙上,梯子AB的长是3米。若梯子与地面的夹角为α,则梯子顶端到地面的距离BC为( )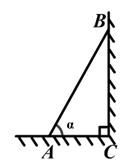 A、3sina米 B、3cosa米。 C、 米 D、 米7. 如图,在△ABC中,∠ACB为钝角。用直尺和圆规在边AB上确定一点D。使∠ADC=2∠B,则符合要求的作图痕迹是( )A、
A、3sina米 B、3cosa米。 C、 米 D、 米7. 如图,在△ABC中,∠ACB为钝角。用直尺和圆规在边AB上确定一点D。使∠ADC=2∠B,则符合要求的作图痕迹是( )A、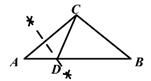 B、
B、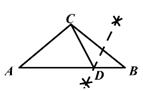 C、
C、 D、
D、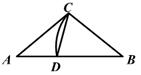 8. 如图,在平面直角坐标系中,Rt△ABC的顶点A、C的坐标分别为(0,3)、(3,0)。∠ACB=90°,AC=2BC,函数y= (k>0,x>0)的图象经过点B,则k的值为( )
8. 如图,在平面直角坐标系中,Rt△ABC的顶点A、C的坐标分别为(0,3)、(3,0)。∠ACB=90°,AC=2BC,函数y= (k>0,x>0)的图象经过点B,则k的值为( )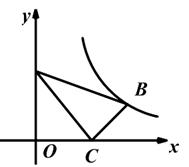
A、 B、9 C、 D、二、填空题(本大题共6小题,每小题3分,共18分)
-
9. 计算:3 - =10. 分解因式:ab+2b=11. 一元二次方程x2-3x+1=0根的判别式的值为12. 如图,直线MN∥PQ,点A、B分别在MN、PQ上,∠MAB=33°。过线段AB上的点C作CD⊥AB交PQ于点D,则∠CDB的大小为 度。
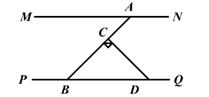 13. 如图,有一张矩形纸片ABCD,AB=8,AD=6。先将矩形纸片ABCD折叠,使边AD落在边AB上,点D落在点E处,折痕为AF;再将△AEF沿EF翻折,AF与BC相交于点G,则△GCF的周长为。
13. 如图,有一张矩形纸片ABCD,AB=8,AD=6。先将矩形纸片ABCD折叠,使边AD落在边AB上,点D落在点E处,折痕为AF;再将△AEF沿EF翻折,AF与BC相交于点G,则△GCF的周长为。 14. 如图,在平面直角坐标系中,抛物线y=ax2-2ax+ (a>0)与y轴交于点A,过点A作x轴的平行线交抛物线于点M。P为抛物线的顶点。若直线OP交直线AM于点B,且M为线段AB的中点,则a的值。
14. 如图,在平面直角坐标系中,抛物线y=ax2-2ax+ (a>0)与y轴交于点A,过点A作x轴的平行线交抛物线于点M。P为抛物线的顶点。若直线OP交直线AM于点B,且M为线段AB的中点,则a的值。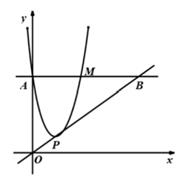
三、解答题(本大题共10小题,共78分)
-
15. 先化简,再求值:(2a+1)2-4a(a-1),其中a=16. 一个不透明的口袋中有三个小球,每个小球上只标有一个汉字,分别是“家”、“家”、“乐”,除汉字外其余均相同。小新同学从口袋中随机摸出一个小球,记下汉字后放回并搅匀;再从口袋中随机摸出一个小球记下汉字。用画树状图(或列表)的方法,求小新同学两次摸出小球上的汉字相同的概率17. 为建国70周年献礼,某灯具厂计划加工9000套彩灯。为尽快完成任务,实际每天加工彩灯的数量是原计划的1.2倍,结果提前5天完成任务。求该灯具厂原计划每天加工这种彩灯的数量。18. 如图,四边形ABCD是正方形。以边AB为直径作⊙O,点E在BC边上,连结AE交⊙O于点F,连结BF并延长交CD于点G
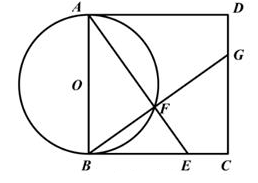 (1)、求证:△ABE≌△BCG(2)、若∠AEB=55°,OA=3,求 的长。(结果保留π)19. 网上学习越来越受到学生的喜爱。某校信息小组为了解七年级学生网上学习的情况,从该校七年级随机抽取20名学生,进行了每周网上学习时间的调查,数据如下(单位:时)
(1)、求证:△ABE≌△BCG(2)、若∠AEB=55°,OA=3,求 的长。(结果保留π)19. 网上学习越来越受到学生的喜爱。某校信息小组为了解七年级学生网上学习的情况,从该校七年级随机抽取20名学生,进行了每周网上学习时间的调查,数据如下(单位:时)3
2.5
0.6
1.5
1
2
2
3.3
2.5
1.8
2.5
2.2
3.5
4
1.5
2.5
3.1
2.8
3.3
2.4
整理上面的数据,得到表格如下:
网上学习时间x(时)
0<x≤1
1<x≤2
2<x≤3
3<x≤4
人数
2
5
8
5
样本数据的平均数、中位数、众数如下表所示:
统计量
平均数
中位数
众数
数值
2.4
m
n
根据以上信息,解答下列问题
(1)、上表中的中位数m的值为 , 众数n的值为 。(2)、用样本中的平均数估计该校七年级学生平均每人一学期(按18周计算)网上学习的时间。(3)、已知该校七年级有200名学生,估计每周网上学习时间超过2小时的学生人数。20. 图①、图②、图③均是6×6的正方形网格,每个小正方形的顶点称为格点,小正方形的边长为1,点A、B、C、D、E、F均在格点上。在图①、图②、图③中,只用无刻度的直尺,在给定的网格中按要求画图,所画图形的顶点均在格点上,不要求写出画法。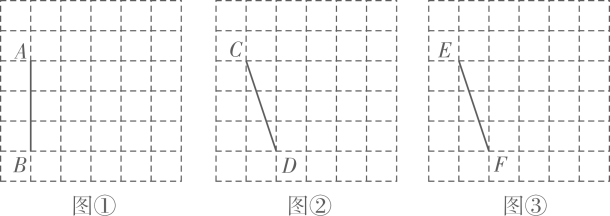 (1)、在图①中以线段AB为边画一个△ABM,使其面积为6。(2)、在图②中以线段CD为边画一个△CDN,使其面积为6。(3)、在图③中以线段EF为边画一个四边形EFGH,使其面积为9,且∠EFG=90°21. 已知A、B两地之间有一条长270千米的公路。甲、乙两车同时出发,甲车以60千米/时的速度沿此公路从A地匀速开往B地,乙车从B地沿此公路匀速开往A地,两车分别到达目的地后停止。甲、乙两车相距的路程y(千米)与甲车的行驶时间x(时)之间的函数关系如图所示
(1)、在图①中以线段AB为边画一个△ABM,使其面积为6。(2)、在图②中以线段CD为边画一个△CDN,使其面积为6。(3)、在图③中以线段EF为边画一个四边形EFGH,使其面积为9,且∠EFG=90°21. 已知A、B两地之间有一条长270千米的公路。甲、乙两车同时出发,甲车以60千米/时的速度沿此公路从A地匀速开往B地,乙车从B地沿此公路匀速开往A地,两车分别到达目的地后停止。甲、乙两车相距的路程y(千米)与甲车的行驶时间x(时)之间的函数关系如图所示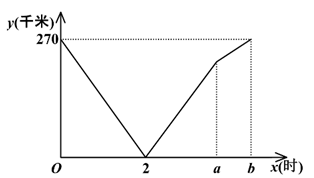 (1)、乙车的速度为千米/时,a= , b= 。(2)、求甲、乙两车相遇后y与x之间的函数关系式(3)、当甲车到达距B地70千米处时,求甲、乙两车之间的路程22. 教材呈现:下图是华师版九年级上册数学教材第78页的部分内容。
(1)、乙车的速度为千米/时,a= , b= 。(2)、求甲、乙两车相遇后y与x之间的函数关系式(3)、当甲车到达距B地70千米处时,求甲、乙两车之间的路程22. 教材呈现:下图是华师版九年级上册数学教材第78页的部分内容。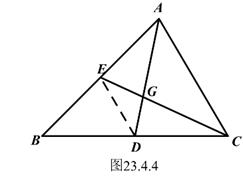
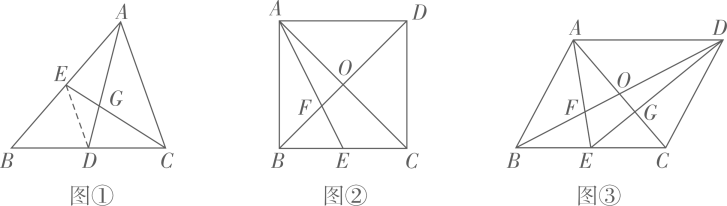 (1)、例2如图23.4.4,在△ABC中,D、E分别是边BC、AB的中点,AD,CE相交于点G。求证:
(1)、例2如图23.4.4,在△ABC中,D、E分别是边BC、AB的中点,AD,CE相交于点G。求证:证明:连结ED。
请根据教材提示,结合图①,写出完整的证明过程结论应用:
(2)、在 ABCD中,对角线AC、BD交于点O,E为边BC的中点,AE、BD交于点F。
如图②,若 ABCD为正方形,且AB=6,则OF的长为。
(3)、如图③,连结DE交AC于点G若四边形OFEG的面积为 ,则 ABCD的面积为。
23. 如图,在Rt△ABC中,∠C=90°,AC=20,BC=15。点P从点A出发,沿AC向终点C运动,同时点Q从点C出发,沿射线CB运动,它们的速度均为每秒5个单位长度,点P到达终点时,P、Q同时停止运动。当点P不与点A、C重合时,过点P作PN⊥AB于点N,连结PQ,以PN、PQ为邻边作 PQMN。设 PQMN与△ABC重叠部分图形的面积为S。点P的运动时间为t秒。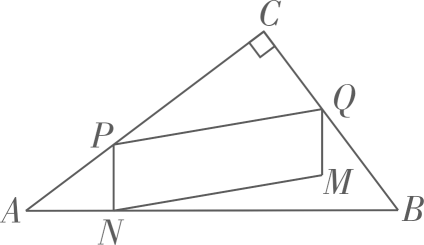 (1)、①AB的长为;
(1)、①AB的长为;②PN的长用含t的代数式表示为。
(2)、当 PQMN为矩形时,求t的值(3)、当 PQMN与△ABC重叠部分图形为四边形时,求S与t之间的函数关系式(4)、当过点P且平行于BC的直线经过 PQMN一边中点时,直接写出t的值24. 已知函数y= (n为常数)(1)、当n=5,①点P(4,b)在此函数图象上,求b的值
②求此函数的最大值
(2)、已知线段AB的两个端点坐标分别为4(2,2)、B(4,2),当此函数的图象与线段AB只有一个交点时,直接写出n的取值范围.(3)、当此函数图象上有4个点到x轴的距离等于4时,求n的取值范围.