四川省自贡市2019年中考数学试卷
试卷更新日期:2019-07-01 类型:中考真卷
一、单选题
-
1. 的倒数是( )A、 B、 C、 D、2. 近年来,中国高铁发展迅速,高铁技术不断走出国门,成为展示我国实力的新名片.现在中国高速铁路营运里程将达到23000公里,将23000用科学记数法表示应为( )A、 B、 C、 D、3. 下列图案中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 在5轮“中国汉字听写大赛”选拔赛中,甲、乙两位同学的平均分都是90分,甲的成绩方差是15,乙的成绩的方差是3,下列说法正确的是( )A、甲的成绩比乙的成绩稳定 B、乙的成绩比甲的成绩稳定 C、甲、乙两人的成绩一样稳定 D、无法确定甲、乙的成绩谁更稳定5. 下图是水平放置的全封闭物体,则它的俯视图是( )
4. 在5轮“中国汉字听写大赛”选拔赛中,甲、乙两位同学的平均分都是90分,甲的成绩方差是15,乙的成绩的方差是3,下列说法正确的是( )A、甲的成绩比乙的成绩稳定 B、乙的成绩比甲的成绩稳定 C、甲、乙两人的成绩一样稳定 D、无法确定甲、乙的成绩谁更稳定5. 下图是水平放置的全封闭物体,则它的俯视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 6. 已知三角形的两边分别为1和4,第三边长为整数 ,则该三角形的周长为( )A、7 B、8 C、9 D、107. 实数 在数轴上对应点的位置如图所示,则下列判断正确的是( )
6. 已知三角形的两边分别为1和4,第三边长为整数 ,则该三角形的周长为( )A、7 B、8 C、9 D、107. 实数 在数轴上对应点的位置如图所示,则下列判断正确的是( )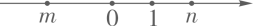 A、 B、 C、 D、8. 关于 的一元二次方程 无实数根,则实数 的取值范围是( )A、 B、 C、 D、9. 如一次函数 与反比例函数 的图像如图所示,则二次函数 的大致图象是 ( )
A、 B、 C、 D、8. 关于 的一元二次方程 无实数根,则实数 的取值范围是( )A、 B、 C、 D、9. 如一次函数 与反比例函数 的图像如图所示,则二次函数 的大致图象是 ( )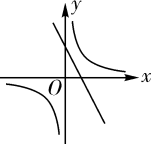 A、
A、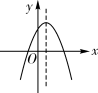 B、
B、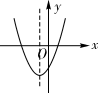 C、
C、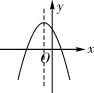 D、
D、 10. 均匀的向一个容器内注水,在注水过程中,水面高度 与时间 的函数关系如图所示,则该容器是下列中的( )
10. 均匀的向一个容器内注水,在注水过程中,水面高度 与时间 的函数关系如图所示,则该容器是下列中的( ) A、
A、 B、
B、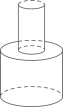 C、
C、 D、
D、 11. 如图中有两张型号完全一样的折叠式饭桌,将正方形桌面边上的四个弓形翻折起来后,就能形成一个圆形桌面(可以近似看作正方形的外接圆),正方形桌面与翻折成圆形桌面的面积之比最接近( )
11. 如图中有两张型号完全一样的折叠式饭桌,将正方形桌面边上的四个弓形翻折起来后,就能形成一个圆形桌面(可以近似看作正方形的外接圆),正方形桌面与翻折成圆形桌面的面积之比最接近( ) A、 B、 C、 D、12. 如图,已知 两点的坐标分别为 ,点 分别是直线 和x轴上的动点, ,点 是线段 的中点,连接 交 轴于点 ;当⊿ 面积取得最小值时, 的值是( )
A、 B、 C、 D、12. 如图,已知 两点的坐标分别为 ,点 分别是直线 和x轴上的动点, ,点 是线段 的中点,连接 交 轴于点 ;当⊿ 面积取得最小值时, 的值是( )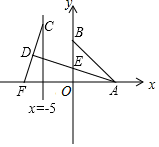 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 如图,直线 被直线 所截, ∥ , ;则 =.
 14. 在一次12人参加的数学测试中,得100分、95分、90分、85分、75分的人数分别为1、3、4、2、2,那么这组数据的众数是.15. 分解因式: = .16. 某活动小组购买4个篮球和5个足球,一共花费了466元,其中篮球的单价比足球的单价多4元,求篮球的单价和足球的单价.设篮球的单价为 元,足球的单价为 元,依题意,可列方程组为 .17. 如图,在 △ 中, , ∥ , 的平分线 交 于 , = .
14. 在一次12人参加的数学测试中,得100分、95分、90分、85分、75分的人数分别为1、3、4、2、2,那么这组数据的众数是.15. 分解因式: = .16. 某活动小组购买4个篮球和5个足球,一共花费了466元,其中篮球的单价比足球的单价多4元,求篮球的单价和足球的单价.设篮球的单价为 元,足球的单价为 元,依题意,可列方程组为 .17. 如图,在 △ 中, , ∥ , 的平分线 交 于 , = . 18. 如图,由10个完全相同的正三角形构成的网格图中, 如图所示,则 =.
18. 如图,由10个完全相同的正三角形构成的网格图中, 如图所示,则 =.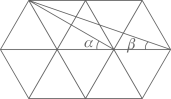
三、解答题
-
19. 计算: .20. 解方程: .21. 如图,⊙ 中,弦 与 相交于点 , ,连接 .

求证:
(1)、 ;(2)、 .22. 某校举行了创建全国文明城市知识竞赛活动,初一年级全体同学参加了竞赛.收集数据:现随机抽取初一年级30名同学“创文知识竞赛”成绩,分数如下(单位:分):90
85
68
92
81
84
95
93
87
89
78
99
89
85
97
88
81
95
86
98
95
93
89
86
84
87
79
85
89
82
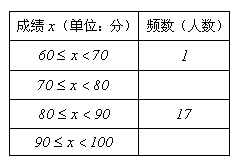
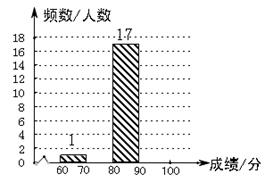 (1)、请将图表中空缺的部分补充完整;(2)、学校决定表彰“创文知识竞赛”成绩在90分以上的同学,根据上表统计结果估计该校初一年级360人中,约有多少人将获得表彰;(3)、“创文知识竞赛”中,受到表彰的小红同学得到了印有龚扇、剪纸、彩灯、恐龙图案的四枚纪念章,她从中选取两枚送给弟弟,则小红送给弟弟的两枚纪念章中,恰好有恐龙图案的概率是 .23. 如图,在平面直角坐标系中,一次函数 的图象与反比例函数 的图象相交于第一、三象限内的 两点,与 轴交于点 .
(1)、请将图表中空缺的部分补充完整;(2)、学校决定表彰“创文知识竞赛”成绩在90分以上的同学,根据上表统计结果估计该校初一年级360人中,约有多少人将获得表彰;(3)、“创文知识竞赛”中,受到表彰的小红同学得到了印有龚扇、剪纸、彩灯、恐龙图案的四枚纪念章,她从中选取两枚送给弟弟,则小红送给弟弟的两枚纪念章中,恰好有恐龙图案的概率是 .23. 如图,在平面直角坐标系中,一次函数 的图象与反比例函数 的图象相交于第一、三象限内的 两点,与 轴交于点 . (1)、求该反比例函数和一次函数的解析式;(2)、在 轴上找一点 使 最大,求 的最大值及点 的坐标;(3)、直接写出当 时, 的取值范围.24. 阅读下列材料:小明为了计算 的值 ,采用以下方法:
(1)、求该反比例函数和一次函数的解析式;(2)、在 轴上找一点 使 最大,求 的最大值及点 的坐标;(3)、直接写出当 时, 的取值范围.24. 阅读下列材料:小明为了计算 的值 ,采用以下方法:设 ①
则 ②
②-①得
∴
(1)、 = ;(2)、 = ;(3)、求1+a+a2+.....+an的和( , 是正整数,请写出计算过程 ).
25. 如图

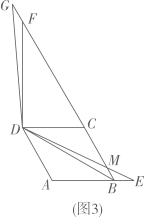 (1)、如图1, 是正方形 边 上的一点,连接 ,将 绕着点 逆时针旋转90°,旋转后角的两边分别与射线 交于点 和点 .
(1)、如图1, 是正方形 边 上的一点,连接 ,将 绕着点 逆时针旋转90°,旋转后角的两边分别与射线 交于点 和点 .①线段 和 的数量关系是;
②写出线段 和 之间的数量关系.
(2)、当四边形 为菱形, ,点 是菱形 边 所在直线上的一点,连接 ,将 绕着点 逆时针旋转120°,旋转后角的两边分别与射线 交于点 和点 .①如图2,点 在线段上时,请探究线段 和 之间的数量关系,写出结论并给出证明;
②如图3,点 在线段 的延长线上时, 交射线 于点 ;若 ,直接写出线段 的长度.
26. 如图,已知直线 与抛物线 : 相交于 和点 两点.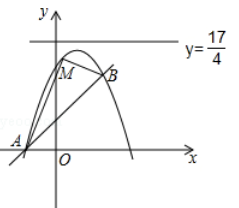
(1)、求抛物线 的函数表达式;(2)、若点 是位于直线 上方抛物线上的一动点,以 为相邻两边作平行四边形 ,当平行四边形 的面积最大时,求此时四边形 的面积 及点 的坐标;(3)、在抛物线 的对称轴上是否存在定点 ,使抛物线 上任意一点 到点 的距离等于到直线 的距离,若存在,求出定点 的坐标;若不存在,请说明理由.