山东省聊城市2019年中考数学试卷
试卷更新日期:2019-07-01 类型:中考真卷
一、单选题
-
1. 的相反数是( )A、 B、 C、 D、2. 如图所示的几何体的左视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 如果分式 的值为0,那么 的值为( )A、-1 B、1 C、-1或1 D、1或04. 在光明中学组织的全校师生迎“五四”诗词大赛中,来自不同年级的25名参赛同学的得分情况如图所示.这些成绩的中位数和众数分别是( )
3. 如果分式 的值为0,那么 的值为( )A、-1 B、1 C、-1或1 D、1或04. 在光明中学组织的全校师生迎“五四”诗词大赛中,来自不同年级的25名参赛同学的得分情况如图所示.这些成绩的中位数和众数分别是( )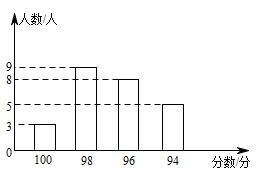 A、96分,98分 B、97分,98分 C、98分,96分 D、97分,96分5. 下列计算正确的是( )A、 B、 C、 D、6. 下列各式不成立的是( )A、 B、 C、 D、7. 若不等式组 无解,则 的取值范围为( )A、 B、 C、 D、8. 如图, 是半圆 的直径, , 是 上两点,连接 , 并延长交于点 ,连接 , ,如果 ,那么 的度数为( )
A、96分,98分 B、97分,98分 C、98分,96分 D、97分,96分5. 下列计算正确的是( )A、 B、 C、 D、6. 下列各式不成立的是( )A、 B、 C、 D、7. 若不等式组 无解,则 的取值范围为( )A、 B、 C、 D、8. 如图, 是半圆 的直径, , 是 上两点,连接 , 并延长交于点 ,连接 , ,如果 ,那么 的度数为( )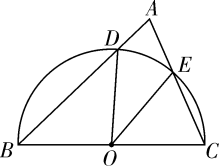 A、 B、 C、 D、9. 若关于 的一元二次方程 有实数根,则 的取值范围为( )A、 B、 且 C、 D、 且10. 某快递公司每天上午9:00~10:00为集中揽件和派件时段,甲仓库用来揽收快件,乙仓库用来派发快件,该时段内甲,乙两仓库的快件数量 (件)与时间 (分)之间的函数图象如图所示,那么当两仓库快递件数相同时,此刻的时间为( )
A、 B、 C、 D、9. 若关于 的一元二次方程 有实数根,则 的取值范围为( )A、 B、 且 C、 D、 且10. 某快递公司每天上午9:00~10:00为集中揽件和派件时段,甲仓库用来揽收快件,乙仓库用来派发快件,该时段内甲,乙两仓库的快件数量 (件)与时间 (分)之间的函数图象如图所示,那么当两仓库快递件数相同时,此刻的时间为( )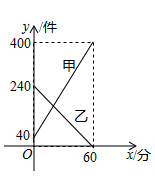 A、9:15 B、9:20 C、9:25 D、9:3011. 如图,在等腰直角三角形 中, ,一个三角尺的直角顶点与 边的中点 重合,且两条直角边分别经过点 和点 ,将三角尺绕点 按顺时针方向旋转任意一个锐角,当三角尺的两直角边与 , 分别交于点 , 时,下列结论中错误的是( )
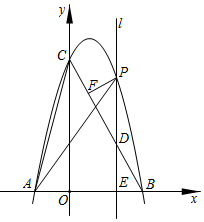
A、9:15 B、9:20 C、9:25 D、9:3011. 如图,在等腰直角三角形 中, ,一个三角尺的直角顶点与 边的中点 重合,且两条直角边分别经过点 和点 ,将三角尺绕点 按顺时针方向旋转任意一个锐角,当三角尺的两直角边与 , 分别交于点 , 时,下列结论中错误的是( )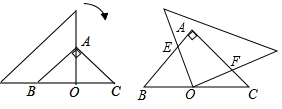 A、 B、 C、 D、12. 如图,在 中, , ,点 在边 上,且 ,点 为 的中点,点 为边 上的动点,当点 在 上移动时,使四边形 周长最小的点 的坐标为( )
A、 B、 C、 D、12. 如图,在 中, , ,点 在边 上,且 ,点 为 的中点,点 为边 上的动点,当点 在 上移动时,使四边形 周长最小的点 的坐标为( )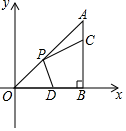 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
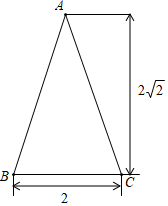
13. 计算: = .14. 如图是一个圆锥的主视图,根据图中标出的数据(单位: ),计算这个圆锥侧面展开图圆心角的度数为 .
 15. 在阳光中学举行的春季运动会上,小亮和大刚报名参加100米比赛,预赛分 四组进行,运动员通过抽签来确定要参加的预赛小组,小亮和大刚恰好抽到同一个组的概率是 .16. 如图,在 中, , , 为 的中位线,延长 至 ,使 ,连接 并延长交 于点 .若 ,则 的周长为 .
15. 在阳光中学举行的春季运动会上,小亮和大刚报名参加100米比赛,预赛分 四组进行,运动员通过抽签来确定要参加的预赛小组,小亮和大刚恰好抽到同一个组的概率是 .16. 如图,在 中, , , 为 的中位线,延长 至 ,使 ,连接 并延长交 于点 .若 ,则 的周长为 .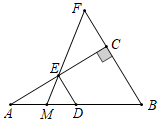 17. 数轴上 两点的距离为4,一动点 从点 出发,按以下规律跳动:第1次跳动到 的中点 处,第2次从 点跳动到 的中点 处,第3次从 点跳动到 的中点 处.按照这样的规律继续跳动到点 ( , 是整数)处,那么线段 的长度为( , 是整数).
17. 数轴上 两点的距离为4,一动点 从点 出发,按以下规律跳动:第1次跳动到 的中点 处,第2次从 点跳动到 的中点 处,第3次从 点跳动到 的中点 处.按照这样的规律继续跳动到点 ( , 是整数)处,那么线段 的长度为( , 是整数).
三、解答题
-
18. 计算: .19. 学习一定要讲究方法,比如有效的预习可大幅提高听课效率.九年级(1)班学习兴趣小组为了了解全校九年级学生的预习情况,对该校九年级学生每天的课前预习时间(单位: )进行了抽样调查.并将抽查得到的数据分成5组,下面是未完成的频数、顿率分布表和频数分布扇形图.
组别
课前预习时间
频数(人数)
频率
1
2
2
0.10
3
16
0.32
4
5
3
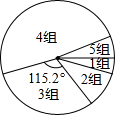
请根据图表中的信息,回答下列问题:
(1)、本次调查的样本容量为 , 表中的 , , ;(2)、试计算第4组人数所对应的扇形圆心角的度数;(3)、该校九年级其有1000名学生,请估计这些学生中每天课前预习时间不少于 的学生人数.20. 某商场的运动服装专柜,对 两种品牌的远动服分两次采购试销后,效益可观,计划继续采购进行销售.已知这两种服装过去两次的进货情况如下表.第一次
第二次
品牌运动服装数/件
20
30
品牌运动服装数/件
30
40
累计采购款/元
10200
14400
(1)、问 两种品牌运动服的进货单价各是多少元?(2)、由于 品牌运动服的销量明显好于 品牌,商家决定采购 品牌的件数比 品牌件数的 倍多5件,在采购总价不超过21300元的情况下,最多能购进多少件 品牌运动服?21. 在如图菱形 中,点 是 边上一点,连接 ,点 是 上的两点,连接 , ,使得 , .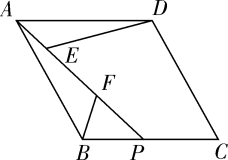 (1)、求证: ;(2)、求证: .22. 某数学兴趣小组要测量实验大楼部分楼体的高度(如图①所示, 部分),在起点 处测得大楼部分楼体 的顶端 点的仰角为 ,底端 点的仰角为 ,在同一剖面沿水平地面向前走20米到达 处,测得顶端 的仰角为 (如图②所示),求大楼部分楼体 的高度约为多少米?(精确到1米)(参考数据: , , , , )
(1)、求证: ;(2)、求证: .22. 某数学兴趣小组要测量实验大楼部分楼体的高度(如图①所示, 部分),在起点 处测得大楼部分楼体 的顶端 点的仰角为 ,底端 点的仰角为 ,在同一剖面沿水平地面向前走20米到达 处,测得顶端 的仰角为 (如图②所示),求大楼部分楼体 的高度约为多少米?(精确到1米)(参考数据: , , , , )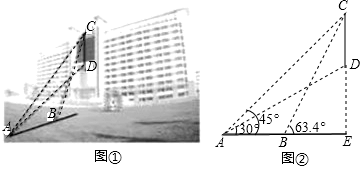 23. 如图,点 , 是直线 与反比例函数 图象的两个交点, 轴,垂足为点 ,已知 ,连接 , , .
23. 如图,点 , 是直线 与反比例函数 图象的两个交点, 轴,垂足为点 ,已知 ,连接 , , .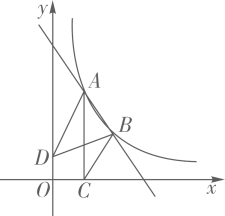 (1)、求直线 的表达式;(2)、 和 的面积分别为 , ,求 .
(1)、求直线 的表达式;(2)、 和 的面积分别为 , ,求 .