山东省菏泽市2019年中考数学试卷
试卷更新日期:2019-07-01 类型:中考真卷
一、单选题
-
1. 下列各数中,最大的数是( )A、 B、 C、0 D、-22. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、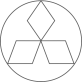 C、
C、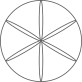 D、
D、 3. 下列运算正确的是( )A、 B、 C、 D、4. 一个几何体的三视图如图所示,则这个几何体的表面积是( )
3. 下列运算正确的是( )A、 B、 C、 D、4. 一个几何体的三视图如图所示,则这个几何体的表面积是( ) A、 B、 C、 D、5. 已知 是方程组 的解,则 的值是( )A、﹣1 B、1 C、﹣5 D、56. 如图, 是 的直径, , 是 上的两点,且 平分 , 分别与 , 相交于点 , ,则下列结论不一定成立的是( )
A、 B、 C、 D、5. 已知 是方程组 的解,则 的值是( )A、﹣1 B、1 C、﹣5 D、56. 如图, 是 的直径, , 是 上的两点,且 平分 , 分别与 , 相交于点 , ,则下列结论不一定成立的是( )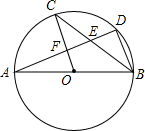 A、 B、 C、 D、7. 在平面直角坐标系中,一个智能机器人接到的指令是:从原点 出发,按“向上→向右→向下→向右”的方向依次不断移动,每次移动1个单位长度,其移动路线如图所示,第一次移动到点 ,第二次移动到点 ……第 次移动到点 ,则点 的坐标是( )
A、 B、 C、 D、7. 在平面直角坐标系中,一个智能机器人接到的指令是:从原点 出发,按“向上→向右→向下→向右”的方向依次不断移动,每次移动1个单位长度,其移动路线如图所示,第一次移动到点 ,第二次移动到点 ……第 次移动到点 ,则点 的坐标是( ) A、 B、 C、 D、8. 如图,正方形 的边长为 ,动点 , 同时从点 出发,在正方形的边上,分别按 , 的方向,都以 的速度运动,到达点 运动终止,连接 ,设运动时间为 , 的面积为 ,则下列图象中能大致表示 与 的函数关系的是( )
A、 B、 C、 D、8. 如图,正方形 的边长为 ,动点 , 同时从点 出发,在正方形的边上,分别按 , 的方向,都以 的速度运动,到达点 运动终止,连接 ,设运动时间为 , 的面积为 ,则下列图象中能大致表示 与 的函数关系的是( )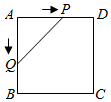 A、
A、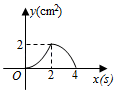 B、
B、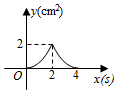 C、
C、 D、
D、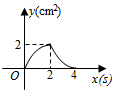
二、填空题
-
9. 计算 的结果是 .10. 已知 ,那么 的值是 .11. 如图, , ,则 的度数是 .
 12. 一组数据4,5,6, 的众数与中位数相等,则这组数据的方差是 .13. 如图, , 是正方形 的对角线 上的两点, , ,则四边形 的周长是 .
12. 一组数据4,5,6, 的众数与中位数相等,则这组数据的方差是 .13. 如图, , 是正方形 的对角线 上的两点, , ,则四边形 的周长是 .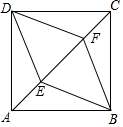 14. 如图,直线 交 轴于点 ,交 轴于点 ,点 是 轴上一动点,以点 为圆心,以1个单位长度为半径作 ,当 与直线 相切时,点 的坐标是 .
14. 如图,直线 交 轴于点 ,交 轴于点 ,点 是 轴上一动点,以点 为圆心,以1个单位长度为半径作 ,当 与直线 相切时,点 的坐标是 .
三、解答题
-
15. 解不等式组:16. 先化简,再求值: ,其中 .17. 如图,四边形 是矩形.
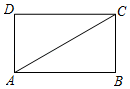 (1)、用尺规作线段 的垂直平分线,交 于点 ,交 于点 (不写作法,保留作图痕迹);(2)、若 , ,求 的长.18. 列方程(组)解应用题:德上高速公路巨野至单县段正在加速建设,预计2019年8月竣工.届时,如果汽车行驶高速公路上的平均速度比在普通公路上的平均速度提高 ,那么行驶81千米的高速公路比行驶同等长度的普通公路所用时间将会缩短36分钟,求该汽车在高速公路上的平均速度.19. 由我国完全自主设计、自主建造的首艘国产航母于2018年5月成功完成第一次海上试验任务.如图,航母由西向东航行,到达 处时,测得小岛 位于它的北偏东 方向,且与航母相距80海里再航行一段时间后到达 处,测得小岛 位于它的西北方向,求此时航母与小岛的距离 的长.
(1)、用尺规作线段 的垂直平分线,交 于点 ,交 于点 (不写作法,保留作图痕迹);(2)、若 , ,求 的长.18. 列方程(组)解应用题:德上高速公路巨野至单县段正在加速建设,预计2019年8月竣工.届时,如果汽车行驶高速公路上的平均速度比在普通公路上的平均速度提高 ,那么行驶81千米的高速公路比行驶同等长度的普通公路所用时间将会缩短36分钟,求该汽车在高速公路上的平均速度.19. 由我国完全自主设计、自主建造的首艘国产航母于2018年5月成功完成第一次海上试验任务.如图,航母由西向东航行,到达 处时,测得小岛 位于它的北偏东 方向,且与航母相距80海里再航行一段时间后到达 处,测得小岛 位于它的西北方向,求此时航母与小岛的距离 的长.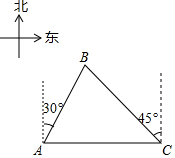 20. 如图, 中,顶点 的坐标是 , 轴, 交 轴于点 ,顶点 的纵坐标是-4, 的面积是24.反比例函数 的图象经过点 和 ,求:
20. 如图, 中,顶点 的坐标是 , 轴, 交 轴于点 ,顶点 的纵坐标是-4, 的面积是24.反比例函数 的图象经过点 和 ,求: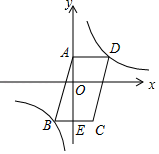 (1)、反比例函数的表达式;(2)、 所在直线的函数表达式.21. 4月23日是世界读书日,习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然之气.”我市某中学响应号召,鼓励师生利用课余时间广泛阅读,该校文学社发起了“读书感悟•分享”比赛活动根据参赛学生的成绩划分为 , , , 四个等级,并绘制了下面不完整的统计图表,根据图表中提供的信息解答下列问题;
(1)、反比例函数的表达式;(2)、 所在直线的函数表达式.21. 4月23日是世界读书日,习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然之气.”我市某中学响应号召,鼓励师生利用课余时间广泛阅读,该校文学社发起了“读书感悟•分享”比赛活动根据参赛学生的成绩划分为 , , , 四个等级,并绘制了下面不完整的统计图表,根据图表中提供的信息解答下列问题;频数
频率
4
0.3
16
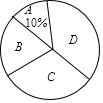 (1)、求 , 的值;(2)、求 等级对应扇形圆心角的度数;(3)、学校要从 等级的学生中随机选取2人参加市级比赛,求 等级中的学生小明被选中参加市级比赛的概率.22. 如图, 是 的直径, 是 的弦,过点 作 的切线,交 的延长线于点 ,过点 作 于点 ,交 的延长线于点 .
(1)、求 , 的值;(2)、求 等级对应扇形圆心角的度数;(3)、学校要从 等级的学生中随机选取2人参加市级比赛,求 等级中的学生小明被选中参加市级比赛的概率.22. 如图, 是 的直径, 是 的弦,过点 作 的切线,交 的延长线于点 ,过点 作 于点 ,交 的延长线于点 .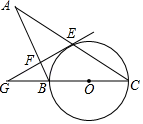 (1)、求证: ;(2)、若 , ,求 的半径.23. 如图, 和 是有公共顶点的等腰直角三角形, .
(1)、求证: ;(2)、若 , ,求 的半径.23. 如图, 和 是有公共顶点的等腰直角三角形, .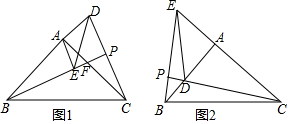 (1)、如图1,连接 , , 的廷长线交 于点 ,交 于点 ,求证: ;(2)、如图2,把 绕点 顺时针旋转,当点 落在 上时,连接 , , 的延长线交 于点 ,若 , ,求 的面积.24. 如图,抛物线与 轴交于 , 两点,与 轴交于点 ,点 的坐标是 , 为抛物线上的一个动点,过点 作 轴于点 ,交直线 于点 ,抛物线的对称轴是直线 .
(1)、如图1,连接 , , 的廷长线交 于点 ,交 于点 ,求证: ;(2)、如图2,把 绕点 顺时针旋转,当点 落在 上时,连接 , , 的延长线交 于点 ,若 , ,求 的面积.24. 如图,抛物线与 轴交于 , 两点,与 轴交于点 ,点 的坐标是 , 为抛物线上的一个动点,过点 作 轴于点 ,交直线 于点 ,抛物线的对称轴是直线 .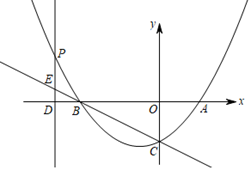 (1)、求抛物线的函数表达式;(2)、若点 在第二象限内,且 ,求 的面积.(3)、在(2)的条件下,若 为直线 上一点,在 轴的下方,是否存在点 ,使 是以 为腰的等腰三角形?若存在,求出点 的坐标;若不存在,请说明理由.
(1)、求抛物线的函数表达式;(2)、若点 在第二象限内,且 ,求 的面积.(3)、在(2)的条件下,若 为直线 上一点,在 轴的下方,是否存在点 ,使 是以 为腰的等腰三角形?若存在,求出点 的坐标;若不存在,请说明理由.