安徽省示范高中培优联盟2018-2019学年高一下学期理数春季联赛试卷
试卷更新日期:2019-06-28 类型:月考试卷
一、单选题
-
1. 设集合 ,集合 ,则 ( )A、 B、 C、 D、2. 实数 , 满足 ,则下列不等式成立的是( )A、 B、 C、 D、3. 已知关于 的方程 的两根之和等于两根之积的一半,则 一定是( )A、直角三角形 B、等腰三角形 C、钝角三角形 D、等边三角形4. 已知 , ,且 ,则向量 与向量 的夹角为( )
A、 B、 C、 D、5. 函数 的零点个数是( )A、1 B、2 C、3 D、46. 的部分图象大致为( )A、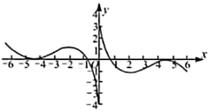 B、
B、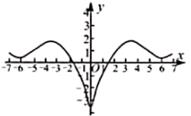 C、
C、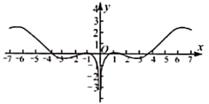 D、
D、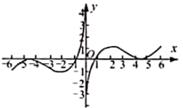 7. 函数 的零点是 和 ,则 ( )A、 B、 C、 D、8. 中, , , ,点 是 内(包括边界)的一动点,且 ,则 的最小值是( )A、 B、 C、3 D、9. 设变量 , 满足约束条件 ,若目标函数 的最小值为1,则 的最小值为( )A、 B、 C、 D、10. 若数列 为等差数列, 为等比数列,且满足: , ,函数 ,则 ( )A、- B、 C、 D、11. 将函数 和直线 的所有交点从左到右依次记为 , ,…, ,若 点坐标为 ,则 ( )A、0 B、2 C、6 D、1012. 对于数列 ,若任意 ,都有 ( 为常数)成立,则称数列 满足 级收敛,若数列 的通项公式为 ,且满足 级收敛,则 的最大值为( )A、6 B、3 C、2 D、0
7. 函数 的零点是 和 ,则 ( )A、 B、 C、 D、8. 中, , , ,点 是 内(包括边界)的一动点,且 ,则 的最小值是( )A、 B、 C、3 D、9. 设变量 , 满足约束条件 ,若目标函数 的最小值为1,则 的最小值为( )A、 B、 C、 D、10. 若数列 为等差数列, 为等比数列,且满足: , ,函数 ,则 ( )A、- B、 C、 D、11. 将函数 和直线 的所有交点从左到右依次记为 , ,…, ,若 点坐标为 ,则 ( )A、0 B、2 C、6 D、1012. 对于数列 ,若任意 ,都有 ( 为常数)成立,则称数列 满足 级收敛,若数列 的通项公式为 ,且满足 级收敛,则 的最大值为( )A、6 B、3 C、2 D、0二、填空题
-
13. 已知函数 为幂函数,则 .14. 已知函数 ,则 .15. 设非零向量 , 的夹角为 ,记 ,若 , 均为单位向量,且 ,则向量 与 的夹角为 .16. 已知函数 , ,若关于 的不等式 恰有两个非负整数解,则实数 的取值范围是 .
三、解答题
-
17. 记 为等比数列 的前 项和, , .
(Ⅰ)求 的通项公式;
(Ⅱ)已知 ,且 ,求 的最小值.
18. 已知函数 的图象的一条对称轴为 .(Ⅰ)求 的最小正周期及单调递增区间;
(Ⅱ)求 在区间 上的最大值和最小值.
19. 如图, 的三个内角 , , 对应的三条边长分别是 , , ,角 为钝角, , , , .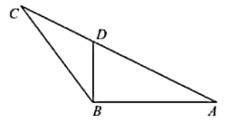
(Ⅰ)求 的值;
(Ⅱ)求 的面积.
20. 2019年春节期间,由于人们燃放烟花爆竹,致使一城镇空气出现污染,须喷洒一定量的去污剂进行处理.据测算,每喷洒1千克的去污剂,空气中释放的浓度 (单位:毫克/立方米)随着时间 (单位:天)变化的函数关系式近似为 ,若多次喷洒,则某一时刻空气中的去污剂浓度为每次投放的去污剂在相应时刻所释放的浓度之和.经测试,当空气中去污剂的浓度不低于4(毫克/立方米)时,它才能起到去污作用.(Ⅰ)若一次喷洒4千克的去污剂,则去污时间可达几天?
(Ⅱ)若第一次喷洒2千克的去污剂,6天后再喷洒 千克的去污剂,要使接下来的4天中能够持续有效去污,试求 的最小值.